Оптико-механическая аналогия в квантовой механике.

Основы квантовой механики.

Исторически, связь между колебаниями и волнами была замечена ещё первыми исследователями, которым бросалось в глаза явное сходство дискретности атомных спектров и дискретности волновых процессов в резонаторах и волновыми процессами. Так, в 1898 г. физик А. Гершель одну из своих работ назвал «О связи между спектром водорода и акустикой». К концу XIX в., благодаря работам Максвелла сформировалось представление о том, что свет и другие виды излучения представляют собой электромагнитные волны. Волновые уравнения Максвелла явились фундаментом волновой теории электромагнитных взаимодействий. На их основе оказалось возможным количественное описание таких оптических явлений, как дисперсия и преломление. С позиций волновой теории можно было объяснить многие экспериментальные данные по взаимодействию электромагнитного излучения с веществом, например, так называемое резонансное испускание и поглощение излучения атомами и молекулами. Однако наиболее важным оказалось открытие М. Планком в 1900 г. дискретной структуры электромагнитного излучения. Анализ экспериментальных данных по термодинамике излучения «абсолютно чёрного тела» привёл к идее порционного обмена энергией между абсолютно чёрным телом (резонатором) и излучением. Им было показано, что для излучения с частотой ω наименьшая порция энергии может быть вычислена на основании формулы вида:

где - оператор Дирака.

такая запись несколько не противоречит хорошо известной формуле:

если учесть, что:

подставляя значение:

в формулу:

получим соответственно:

оператор Дирака , представляет собой экспериментально найденную постоянную, имеющую размерность действия . Объяснение А.Эйнштейном в 1905 г. явления фотоэффекта, явилось одним из подтверждением корпускулярной природы электромагнитного излучения. В соответствии с корпускулярной картиной, электромагнитное излучение с частотой , представляет собой поток частиц – фотонов (квантов света) с энергией:

и импульсом:

В 1922 г. А. Комптон, исследуя рассеяние рентгеновских лучей на электронах (эффект Комптона) и проделав соответствующие вычисления, доказал, что кванты электромагнитного излучения ведут себя как корпускулы (частицы), обладающие энергией и импульсом. Выражение для импульса фотона легко получить, если приравнять между собой два выражения для энергии фотона:

учитывая также выражения вида:

откуда:

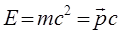
выражения для энергии фотона можно преобразовать к виду:

принимая отношение:

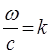
где - волновое число. Учитывая приведенные выше соображение, приходим к выражению вида:

Импульс частицы, строго говоря, векторная величина, поэтому корректнее приведенные формулы записывать не в скалярной, а в векторной форме, т.е.

. Здесь волновое число k имеет смысл волнового вектора, указывающего направление распространения волны. В последнем выражении объединены, казалось бы, два несовместимых свойства излучения – корпускулярная характеристика 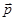и волновая характеристика . Однако де Бройль (1923) разрешил это противоречие, применив оптико-механическую аналогию Гамильтона. Именно де Бройль увидел универсальный характер соотношений:

их справедливость для любой частицы, наделённой количеством движения (импульсом). По-сути де Бройль перевернул эти соотношения, сопоставив механическому импульсу - волновое число , а энергии - частоту .

Учитывая также, что:

будем иметь соответственно:

так как по определению справедливы соотношения вида:

тогда соответственно:

или что то же самое:

преобразование полученного выше выражения:

приводит к уравнению вида:

Последнее выражение представляет собой формулу де Бройля для длины волны микрочастицы, где по определению 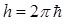. Зная волновое число k, нетрудно записать плоскую гармоническую волну в явном виде. Корпускулярно-волновая природа электромагнитного излучения вскоре была подтверждена Дэвиссоном и Джермером, которые в 1927 г. наблюдали дифракцию электронов на поверхности монокристаллов никеля, которую повторно наблюдал Г. Томсон при прохождении пучка электронов через тонкую золотую фольгу. Из соотношения де Бройля следует условие квантования Бора для орбитального момента импульса. Так, если электрон в модели Бора обладает волновыми свойствами, то эта орбита должна быть такой, чтобы на ней образовывалась стоячая волна; другими словами, длина орбиты должна представлять собой целочисленное, кратное длины волны, т.к. в противном случае интерференция разрушит орбиту, т.е.

учитывая, что:

будем иметь соответственно:

поскольку:

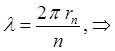
приходим к выражению вида:

поскольку:

будем иметь соответственно:

В 1926 г. руководствуясь оптико-механической аналогией Гамильтона и идеей де Бройля о корпускулярно-волновой природе микрочастиц, Э.Шрёдингер предложил свой вариант квантовой механики – волновую механику. В основе механики Шрёдингера лежат представления об аналогии между механическими колебаниями и волнами. Используя волновое уравнение классической теории электромагнитного излучения и соотношение де Бройля, связывающее импульс частицы с длиной волны , Э. Шрёдингер получил уравнение, описывающее движение микрообъектов в пространстве:

В 1927 г. В. Гейзенберг установил так называемый принцип неопределённости, согласно которому: невозможно одновременно точно осуществить одновременное измерение координаты и импульса микрочастицы. Это означает, в свою очередь, что осуществление измерения одной величины, исключает возможность измерения другой физической величины. При этом, чем точней будет измерена координата микрочастицы, тем больше будет неопределённость в измерении импульса, и наоборот – чем точней будет измерен импульс микрочастицы, тем больше будет неопределённость в определении её координаты. Так, на основании формулы де Бройля, имеем:

поэтому:

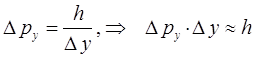
В этом же самом году им была предложена так называемая матричная механика, основная идея которой состояла в том, что каждой наблюдаемой физической величине соответствовала определённая матрица. Э. Шрёдингером было показано, что матричная механика Гейзенберга, в конечном счете, сводится к волновой механике. Результатом этого стало объединение обеих подходов и возникновение квантовой механики. Квантовая механика занимает своеобразное положение в ряду физических теорий. Обычно более общая теория может быть сформулирована логически замкнутым образом не зависимо от менее общей теории, являющейся её предельным случаем. Так, релятивисткая механика может быть построена на основании своих принципов, без всяких ссылок на ньютоновскую механику. Формулировка же основных положений квантовой механики, принципиально невозможна без привлечения механики классической. Таким образом, квантовая механика содержит в себе классическую в качестве своего предельного случая. Мало того, она нуждается в этом самом предельном случае для самого своего обоснования. При этом переход от классической механики к квантовой, осуществляется через механику колебаний и волн по-аналогии с тем, как происходит предельный переход от волновой к геометрической оптике. Необходимо подчеркнуть, что указанный выше предельный переход не только неизбежен, но и необходим. Он позволяет представить квантовую механику не как систему постулатов «загадочного» происхождения, а как стройную физическую теорию с определённым логическим выводом (терминологически и идейно) из классического подхода. Так, при выводе уравнения Шрёдингера, достаточно удобным является рассмотрение движения частицы в центральном поле сил. Характерными примерами систем такого типа является гармонический осциллятор и движение частицы в кулоновском поле сил. Рассмотрим простейший тип колебательного движения – свободные (собственные) незатухающие механические колебания, т.е. такие колебания, которые совершаются без внешнего воздействия за счёт первоначально полученной телом энергии. При рассмотрении колебаний такого вида – пренебрегают силой сопротивления. Простейшим типом колебательного движения являются гармонические колебания, т.е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Рассмотрим одномерное движение частицы (материальной точки) с массой , на которую действует вдоль одной из координатных осей упругая возвращающая сила . Очевидно, при малых отклонениях частицы (материальной точки) от положения равновесия, под действием упругой возвращающей силы 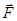, будут совершаться колебания относительно этой точки равновесия. Такую колебательную систему называют гармоническим осциллятором. Примерами гармонического осциллятора являются пружинный (материальная точка на пружине), математический и физический маятники, а также колебательный контур (для токов и напряжений столь малых, что элементы контура можно было бы считать линейными).

Для рассматриваемой системы гармонического осциллятора, очевидно, будут справедливы условия вида:

Пусть у нас имеется некоторое тело массой – m (материальная точка), подвешенное на пружине жёсткостью . В этом положении упругая сила , приложенная к телу, уравновешивает силу тяжести , т.е. в данном случае справедливо равенство вида:

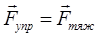
Смещение материальной точки относительно оси (положение равновесия) равно нулю, т.е. . Если к телу приложить некоторую силу 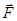, оттянув пружину (сместив данное тело из положения равновесия, при котором ), то тело выйдет из состояния равновесия.

Рис. 1. Модель гармонического осциллятора

При этом на тело будет действовать большая упругая сила , которая будет тем больше, чем больше смещение будет получать подвешенное на пружине тело. Согласно закону Гука, при упругих деформациях возникает сила, направленная к положению равновесия и пропорциональная смещению тела (деформации). Силы, неупругие по природе, но аналогичные по-свойствам, называют квазиупругими. Квазиупругие силы возникают при малых деформациях. Таким образом, изменение упругой силы, пропорционально изменению длины пружины или смещению тела:

здесь k – коэффициент пропорциональности (жёсткость пружины).

Знак минус показывает, что возвращающая сила 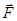всегда направлена в сторону положения равновесия. На основании второго закона Ньютона:

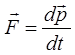
а также учитывая, что:

получим дифференциальное уравнение, описывающее движение материальной точки:

преобразуем полученное выражение к виду:

примем:

откуда:

тогда:

Полученное выражение представляет собой линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами.

В общем случае, линейным дифференциальным уравнением второго порядка называется уравнение первой степени (линейное) относительно неизвестной функции и её производных. Будем записывать его в виде:

где и – постоянные. Функция называется правой частью уравнения. Если функция тождественно равна нулю (как в нашем случае), то такое уравнение называется линейным уравнением без правой части (или однородным). В противном случае – линейным уравнением с правой частью (или неоднородным). Достаточно очевидно, что при и , дифференциальное уравнение:

сводится к уравнению вида:

в данном уравнении:

Теорема 1: «Если q₁(t) и q₂(t) – решения линейного уравнения , то функция вида при любых постоянных c₁ и c₂ , также является решением уравнения. Здесь выражение является линейной комбинацией соответствующих частных решений q₁ и q_2.». Из сказанного выше можно заключить, что если q₁ и q₂ – решения уравнения:

такие, что их отношение не равно постоянной величине:

то линейная комбинация этих функций , является решением дифференциального уравнения. Нахождение общего решения дифференциального уравнения принципиально, т.к. из общего решения при любых заданных условиях может быть найдено частное решение, удовлетворяющее этим условиям. Для проверки линейной независимости функций q₁ и q₂, являющихся частными решениями дифференциального уравнения, необходимо составить и решить так называемый определитель Вронского (Вронскиан) W:

При этом Вронскиан не должен обращаться в нуль, т.е. .

Обычно частные решения дифференциального уравнения ищут в виде показательной функции , где l - постоянная величина. Такой выбор вида частного решения обусловлен тем, что это единственная элементарная функция, все производные которой подобны между собой и к самой функции. Функцию вида называют ещё стандартной подстановкой. Дифференцируя функцию , беря вначале первую, а затем вторую производную:

Возвратимся теперь к исходному дифференциальному уравнению:

очевидно подстановка значения в данное уравнение, даст выражение вида:

Поскольку , то из последнего уравнения следует, что:

такое уравнение относительно l, называется характеристическим уравнением, отвечающим соответствующему дифференциальному уравнению:

,

а функция является стандартной подстановкой (частным решением дифференциального уравнения), с помощью, которой решается исходное дифференциальное уравнение. При этом, будет частным решением соответствующего уравнения лишь в том случае, если l - корень характеристического уравнения. Таким образом, для решения искомого дифференциального уравнения необходимо составить и решить характеристическое уравнение. Чтобы составить характеристическое уравнение, нужно в данном дифференциальном уравнении:

заменить q единицей, а производную искомой функции – величиной l в степени, равной порядку производной l² соответственно.

Следует различать три возможных случая для корней l₁ и l₂ характеристического уравнения (предполагается, что коэффициенты M и N – действительные числа):

· l₁ и l₂ – корни уравнения действительные и различные числа, т.е. .

· l₁ и l₂ - корни уравнения действительные и равные числа, т.е. .

· l₁ и l₂ - корни уравнения комплексные сопряжённые числа: l₁ = a + ib

и l₂ = a - ib ( ).

Учитывая, что:

представим уравнение:

к виду:

Запишем теперь, в соответствии с правилами указанными выше, характеристическое уравнение:

,

l₁ = iw ,

l₂ = - iw

имеем соответственно два независимых решения искомого дифференциального уравнения. Таким образом, решив характеристическое уравнение, мы приходим к выводу о том, что корни уравнения – комплексно сопряжённые числа (третий из выше перечисленных случаев). В соответствии с приведенной выше теоремой об общем решении дифференциального уравнения, в независимости от того являются ли корни характеристического уравнения действительными или комплексными сопряжёнными числами, общее решение имеет вид:

поскольку в нашем случае, корни характеристического уравнения являются комплексными сопряжёнными числами, т.е. имеет место два независимых решения:

l₁ = a + ib,

l₂ = a - ib,

общее решение можно записать в виде:

здесь с₁ и с₂ –произвольные комплексные постоянные. Учитывая, что:

тогда на основании выше приведенных выкладок можно заключить, что:

Учитывая, что общее решение дифференциального уравнения строится как суперпозиция частных решений:

будем иметь соответственно:

здесь частными являются решения вида:

На основании известных из курса линейной алгебры формул Эйлера:

откуда следует, что:

а также принимая, что:

получим соответственно уравнение вида:

поскольку по-определению:

тогда выражение вида:

очевидно, может быть представлено к виду:

Если же принять, что:

тогда будем иметь соответственно:

поскольку:

тогда выражение:

очевидно, может быть представлено к виду:

Таким образом, путём соответствующих преобразований, на основании общего решения дифференциального уравнения:

мы пришли к двум эквивалентным друг другу решениям дифференциального уравнения, записанным в тригонометрической формах:

здесь величина есть амплитуда колебания, характеризующая размах колебательного движения, величину смещения материальной точки от положения равновесия. Аргумент называется фазой колебания, а - начальной фазой колебания в момент времени . Достаточно очевидно, что:

Расстояние, отделяющее колеблющуюся точку от положения равновесия, характеризует величина . В общем случае амплитуда и начальная фаза колебания определяются начальными условиями движения, т.е. положением и скоростью материальной точки в момент времени . Среди различных видов колебательного движения, гармонические колебания являются наиболее простыми. Необходимо отметить, что поскольку величина характеризует смещение материальной точки от положения равновесия, а величина - амплитуду колебательного движения (размах колебания), тогда при условии:

величина будет сводиться к величине, и будет характеризовать, таким образом, максимальное отклонение колеблющейся материальной точки от положения равновесия, т.е. будет справедливо уравнение вида:

и

Необходимо также отметить, что при преобразовании дифференциального уравнения, описывающего колебания гармонического осциллятора, величина была введена чисто формально, в то время как она имеет глубокий физический смысл, определяя частоту колебаний.

учитывая, что:

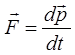
тогда соответственно:

принимая что:

имеем:

Величина называется круговой (циклической) частотой. Выведенное для гармонического осциллятора дифференциальное уравнение, показывает, что данная величина зависит от жёсткости пружины и массы материальной точки. Аналогичная угловой скорости , она связывает линейную скорость и период колебаний, представляя, таким образом, число периодов колебаний, за которые фаза колебания получит приращение . Это становится очевидным из следующих рассуждений.

Поскольку формально:

тогда соответственно:

Очевидно, чем больше по величине будет круговая (циклическая) частота, тем меньше будет величина периода колебательного движения. Проводя аналогию между угловой скоростью и циклической частотой, можно увидеть, что чем больше будет скорость, с которой колеблющаяся точка совершит полный оборот на при своём движении, получая, таким образом, приращение , тем за меньшее время будет совершено системой колебательное движение. Рассмотрим теперь более сложный случай – волновой процесс. Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом. При распространении волны, частицы среды не передвигаются вместе с волной, а колеблются около положений своих равновесий. При этом вместе с волной от частицы к частице среды передаётся лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы – является перенос энергии в отсутствии переноса вещества. Можно выделить следующие типы волн: волны на поверхности жидкости, упругие (механические) волны и электромагнитные волны. Упругие волны бывают продольными и поперечными. Если частицы колеблются по той же прямой, вдоль которой распространяется колебание, то такая волна называется продольной; если колебания частиц перпендикулярны к направлению распространения колебаний, то волна называется поперечной. Таким образом, продольные волны могут распространяться лишь в том случае, если в среде возникают силы упругости при деформации сжатия и растяжения. Если же при сдвиге одного слоя среды по отношению к другому слою возникают упругие силы, стремящиеся возвратить сдвинутый слой в положение равновесия, то в среде могут распространяться поперечные волны. Если такие силы в среде не возникают, то поперечные волны образоваться не могут. Являются ли волны, распространяющиеся в среде, продольными или поперечными – зависит от упругих свойств среды. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны равна тому расстоянию, на которое распространяется данная фаза колебания за период . Имеем соответственно:

учитывая, что:

будем иметь соответственно:

Две волны называют когерентными, если частицы колеблются в одинаковых фазах. Геометрическое место точек, до которых доходят колебания к моменту времени , называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновые поверхности могут быть любой формы. Если волновая поверхность представляет собой совокупность плоскостей, параллельных друг другу, то такая волна называется плоской. Если же волновая поверхность представляет совокупность концентрических сфер, параллельных друг другу, то такая волна будет называться сферической. Пусть в системе происходит волновой процесс и в точке находится начальная фаза колебаний (примем, что оно совершается по закону синуса). Для упрощения выкладок будем рассматривать плоскую волну, распространяющуюся вдоль одной из координатных осей (например, вдоль оси ) – одномерный случай, тогда будем иметь соответственно:

после подстановки начального условия , будем иметь:

Возьмём на прямой произвольную точку М, лежащую от начала координат (точка ) на расстоянии . Очевидно, что колебания распространяясь от точки , дойдут до точки М через промежуток времени . Тогда, следовательно:

Таким образом, точка М начнёт колебаться на время позже точки , поэтому:

или с учётом соотношения вида:

получим соответственно:

Полученное выше соотношение, представляет собой уравнение плоской волны, распространяющейся вдоль оси . Фронт такой волны будет представлять собой плоскость. Данное уравнение задаёт смещением как функцию времени и расстояния от точки М до центра колебаний лежащего в точке . Очевидно, что аргумент:

есть не что иное как фаза волны . Если представить себе волну, распространяющуюся в направлении, обратном рассмотренному выше, тогда уравнение плоской бегущей волны вида:

должно быть заменено уравнением вида:

Полученные нами выше уравнения для двух взаимообратных плоских бегущих волн:

могут быть преобразованы далее к виду:

учитывая выражения вида:

будем иметь соответственно:

здесь величина вида:

представляет собой волновой вектор. Тогда соответствующие уравнения для плоских бегущих волн можно представить к виду:

Для последующих выкладок удобней представить полученные выражения в экспоненциальной форме. При этом ограничимся рассмотрением лишь таких волн, которые распространяются вдоль оси в прямом направлении.

Уравнение де Бройля (для случая плоских волн), есть одно из возможных решений дифференциального уравнения в частных производных, описывающее процесс распространения возмущения (колебания) в среде. Такое уравнение называется волновым уравнением. Для его получения необходимо дважды продифференцировать полученное выше уравнение плоской бегущей волны по координате и дважды по времени , тогда:

 

с учётом выражений вида:

будем иметь соответственно:

Аналогично получаем значение второй производной по времени:

с учётом выражений вида:

будем иметь соответственно:

Таким образом, в ходе проделанных операций дифференцирования, мы пришли к выражениям вида:

Выражая из полученных выражений величину и приравнивая между собой общую переменную , будем иметь соответственно:

аналогично:

имеем таким образом:

откуда следует, что:

с учётом выражения вида:

будем иметь соответственно:

для случая электромагнитных волн, имеем:

тогда соответственно:

Полученное нами выше волновое уравнение описывает распространение плоской бегущей электромагнитной волны вдоль оси . Однако оно остаётся справедливым и для трёхмерного случая. Распространяя данное уравнение для случая трёх пространственных координат, полученное выше волновое уравнение можно записать в обобщённом виде:

Более строгий вывод волнового уравнения можно получить на основании электромагнитной теории Максвелла, которая была разработана методом последовательного теоретического и математического обобщения основных экспериментальных законов электрических и магнитных явлений: закона Кулона в обобщённой форме на основании теоремы Гаусса, закона полного тока и закона электромагнитной индукции. Данная теория, феноменологическая по своей природе, выявила единство и тесную взаимосвязь электрических и магнитных полей, не связывая при этом характер и специфику их взаимодействия с внутренними механизмами взаимодействия поля и вещества. В отличие от господствовавших на то время ошибочных взглядов, основывавшихся на концепции дальнодействия, допускающих мгновенное распространение в пространстве взаимодействий между заряженными частицами и не учитывавших роль промежуточной среды – поля, теория Дж. Максвелла напротив, показала, что электромагнитные взаимодействия могут передаваться от одной точки пространства к другой материальным агентом – электромагнитным полем – с конечной скоростью, равной скорости света (концепция близкодействия). В 1865 г. Дж. Максвелл теоретически показал, что электромагнитное поле в виде электромагнитных волн может распространяться в пространстве с конечной скоростью, равной скорости света в вакууме . В общем случае под электромагнитным полем понимают форму материи, через которую осуществляется взаимодействие между электрически заряженными частицами. Понятие поля (электрического и магнитного) было введено в 1830 г. М. Фарадеем. Концепция поля стала возрождением теории близкодействия, основателем которой был Р. Декарт. В 60-х г.г. XIX в. развивая идеи М. Фарадея относительно природы электромагнитного поля, Дж. Максвелл раскрыл его природу и сформулировал основные законы. Согласно данных представлений заряженные частицы или токи образуют во всех точках окружающего пространства поле, действующее на другие заряженные частицы или токи, помещённые в произвольную точку этого пространства. Электромагнитное поле в вакууме характеризуется векторами напряжённости электрического поля и индукции магнитного поля . Этими векторами определяются силы, действующие со стороны электромагнитного поля на подвижные и неподвижные электрически заряженные частицы. В среде электромагнитное поле характеризуется двумя дополнительными параметрами: вектором смещения (индукции) электрического поля и вектором напряжённости магнитного поля . В теории Максвелла раскрывается электромагнитная природа света и таким образом собственно электрические и магнитные явления рассматриваются в совокупности и сведены воедино. Единство электрических и магнитных полей, наличие тесной взаимосвязи между ними позволили по-новому взглянуть на природу электромагнитных явлений и обобщить накопленные экспериментальные данные. Ещё М. Фарадей экспериментально выявил, что изменение во времени магнитного поля приводит к возникновению вихревого электрического поля (явление электромагнитной индукции). Из курса электродинамики известно, что источниками электрического поля могут быть либо электрические заряды, либо переменные во времени магнитные поля. В первом случае поле электрических зарядов описывается обобщённым на основании теоремы Гаусса законом Кулона, который можно представить дифференциальным уравнением вида:

учитывая, что:

оно может быть преобразовано далее к виду:

Последнее выражение представляет собой обобщённый закон Кулона, описывающий распределение зарядов в элементарном объёме вещества. Описываемое таким образом поле является потенциальным, циркуляция вектора напряжённости по произвольному замкнутому контуру равна нулю:

Силовые линии такого поля являются незамкнутыми: они выходят из позитивных зарядов (источников поля) или идут из бесконечности и входят в негативные заряды (стоки поля) или уходят в бесконечность. По этой причине электростатическое поле не может обеспечить непрерывное движение электрических зарядов вдоль замкнутых проводников, т.е. обеспечить направленное движение зарядов по замкнутому контуру. Для того чтобы в таком проводящем замкнутом контуре возникал и поддерживался длительное время электрический ток, необходимо наличие сторонних сил (сил неэлектрической природы), тогда очевидно:

где - электродвижущая сила (ЭДС). Электрическое поле, которое возникает в контуре вследствие работы сторонних сил, существенно отличается от электростатического поля неподвижных зарядов. Линии напряжённости такого поля являются замкнутыми вдоль проводящего контура, по этой причине циркуляция такого вектора напряжённости будет принимать отличные от нуля значения, т.е.

Электрические поля, возбуждаемые переменным магнитным полем являются вихревыми (соленоидальными). Для таких полей циркуляция вектора напряжённости по произвольному замкнутому контуру отлична от нуля и равна скорости изменения магнитного потока, пронизывающего произвольную поверхность, опирающуюся на контур интегрирования. Такие вихревые поля обуславливают непрерывное движение электрических зарядов вдоль замкнутых проводников, помещённых в это поле, т.е. приводят к возникновению индукционного тока. В основе электродинамики переменных полей лежит закон электромагнитной индукции, открытый в 1831 г. М Фарадеем, суть которого состоит в возникновении тока в произвольном замкнутом проводящем контуре при изменении магнитного потока, пронизывающего этот контур. Ещё в 1820 г. Х.Эрстед открыл, что вокруг проводников с током возникает магнитное поле. В том же году А. Ампер установил, что на проводники с током действует пондемоторная сила – механическая сила, не являющаяся по своей природе механической. Результаты этих исследований стали основой допущения, что электрическое поле можно получить за счёт магнитного. В 1831 г. М. Фарадей заметил, что электрические эффекты возникают только при изменении магнитного поля, т.е. при наложении переменного магнитного поля. Так, если в одном проводнике изменять электрический ток, то в соседнем также будет возникать электрический ток. К аналогичному результату можно прийти, если возле замкнутого проводника перемещать магнит. При этом электрический ток в обоих случаях будет наводиться (индуцироваться) переменным магнитным полем. Такой ток называют индукционным, а явление возникновения индукционного тока в проводнике под действием переменного магнитного поля - явлением электромагнитной индукции. Таким образом, открытие М. Фарадея состояло в том, что индукционный ток в замкнутом контуре может возникнуть во время движения проводящего контура в поле магнита, во время движения магнита относительно замкнутого контура, а также во время изменения тока в катушке, создающей магнитное поле. Всё это сводится к одному общему правилу: «Индукционный ток в замкнутом проводящем контуре возникает каждый раз при изменении магнитного потока пронизывающего замкнутый контур». Для того чтобы электрические заряды (электроны в проводнике) пришли в направленное движение, на них должны действовать сторонние силы , возникающие там, где имеет место изменение магнитного поля. Это в свою очередь привело к открытию закона, устанавливающего взаимосвязь между электрическим и магнитным полями. В тех областях, где имеет место изменение магнитного поля, возникает вихревое электрическое поле. Именно такое электрическое поле, возникающее в переменных магнитных полях, приводит к упорядоченному движению электронов в проводящем контуре, определяя, таким образом, возникновение ЭДС индукции при всяком изменении магнитного потока. Рассмотрим причину возникновения индукционного тока при наложении переменного магнитного поля. Так, в проводнике - проводящем замкнутом контуре, имеются позитивные заряды – ионы кристаллической решётки и свободные электроны проводимости – отрицательно заряженные ионы. При движении проводника в магнитном поле со скоростью , вместе с ним будут перемещаться также и заряды. При этом перемещение зарядов будет определять так называемый конвекционный ток. За направление электрического тока принимается движение положительных зарядов. Поскольку позитивные заряды связаны с кристаллической решёткой проводника и перемещаться не могут, то движущиеся электроны проводимости будут передавать своё движение ионам кристаллической решётки. В постоянном магнитном поле на движущиеся заряды будет действовать сила Лоренца, искривляющая траектории движения зарядов. Последняя направлена противоположно движению этих зарядов и в переменном магнитном поле создавать в проводнике индукционный ток, заряжая один конец проводника позитивно, а другой – негативно. Здесь сила Лоренца будет играть роль сторонних сил, т.е. поскольку по определению:

тогда соответственно:

Вследствие действия сторонних сил (силы Лоренца), проводник заряжается разноимённо, т.е. создаётся разность потенциалов, являющаяся причиной возникновения тока в замкнутом проводящем контуре. Эта разность потенциалов замыкает концы проводника, вследствие чего образовавшуюся систему можно считать замкнутым проводящим контуром. По определению, ЭДС определяется работой сторонних сил при перемещении единичного пробного заряда по замкнутому контуру. Если за замкнутый контур L взять контур произвольного проводника в переменном магнитном поле, тогда:

учитывая, что:

будем иметь соответственно:

здесь - электродвижущая сила (ЭДС) индукции. Для того чтобы установить формулу для вычисления ЭДС индукции, удобно воспользоваться законом сохранения энергии. Впервые такие расчёты были проведены Г. Гельмгольцем. Так, согласно закона Ампера имеем:

тогда под действием силы Ампера для одномерного случая (вдоль одной из координатных осей), работа:

Учитывая также выражение для элементарного потока магнитной индукции:

будем иметь соответственно:

Если сопротивление проводящего контура равно , то согласно закону сохранения энергии, работа источника тока за время будет слагаться из работы нагревания проводника и работы перемещения его в магнитном поле. Поскольку по определению:

или переходя к бесконечно малым, будем иметь соответственно:

учитывая также, что:

Таким образом, в ходе проделанных выше выкладок, приходим соответственно к выражениям вида:

тогда:

Полученное нами выше последнее уравнение представляет собой ту работу, которую выполняю сторонние силы (силы источника тока) за время . Для того чтобы вычислить работу идущую на нагревание проводника при прохождении через него тока силой , необходимо знать падение напряжения на данном участке проводника. Падение напряжения можно вычислить на основании уравнения вида:

или переходя к бесконечно малым величинам, будем иметь:

учитывая, что:

имеем:

На основании закона Ома для участка цепи:

а также, что:

будем иметь соответственно:

Полученное уравнение:

представляет собой аналитическое выражение закона Джоуля – Ленца. Данное уравнение определяет работу, затрачиваемую на нагрев проводника сечением при прохождении через него тока силой . Таким образом, в ходе проделанных выше выкладок, приходим к выражениям для работы:

тогда соответственно будем иметь: