Подставив полученное выражение в (2а) имеем
или 
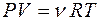, (11)
где NA·k = R =8,31 Дж/моль·К – универсальная молярная газовая постоянная.
Уравнение (11) называется уравнением состояния идеального газа или уравнением Клапейрона-Менделеева.
Как частные случаи из основного уравнения состояния идеального газа можно получить уравнения процессов.
1) Изотермический процесс – процесс при Т=const.
Из (11) имеем, что при Т=const должно быть PV=const
или P1V1 =P2V2 (Закон Бойля–Мариотта)
2) Изобарный процесс – процесс при P = const,
Для данного процесса из (11) получаем
или 
(Закон Гей-Люссака)
3) Изохорный процесс – процесс при V =const .
Для данного процесса из (11) имеем
или 
(Закон Шарля)
IV. Смеси газов. Закон Дальтона.
Для смеси нескольких газов общее число молекул равно сумме молекул отдельных газов: N=N1+N2+...+Nn. Поделив это соотношение на NA, получим:
. (12)
Так как все газы в смеси находятся при одинаковой температуре в одном и том же объеме и двигаются независимо друг от друга, то уравнение (11) можно записать для каждого газа в отдельности
, откуда 
(13)
Величина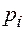 
в данном уравнении называется парциальным давлением. Оно равно давлению, которое имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один.
Подставляя значения 
и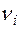 
в уравнение (12) получим
. (14)
Т.е. давление смеси газов равно сумме их парциальных давлений. Уравнение Клапейрона-Менделеева для смеси газов можно записать также в виде:
(15)
где 
- эффективная молярная масса смеси газов. Из данного соотношения получаем
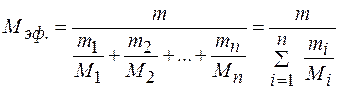(16) Введем массовую концентрацию газа в смеси, как 
. Тогда, поделив числитель и знаменатель правой части выражения (16) на m, получим = 
(17)
Если известны молярные концентрации газов в смеси 
, то, используя, что 
, а 
, получим
. (18)
V.Методика определения молярной массы газа.
Учитывая важность понятия молярной массы в курсе молекулярной физики, в данной лабораторной работе предлагается определить эффективную молярную массу воздуха. Для этой цели возьмем стеклянный сосуд с известным объемом V, заполненный воздухом при атмосферном давлении 
и температуре Т. Состояние воздуха в сосуде близко к состоянию идеального газа и для него можно записать уравнение Клапейрона-Менделеева в виде:
(19)
После откачки воздуха из сосуда до некоторого остаточного давления 
для оставшегося в сосуде воздуха можно записать:
(20)
После вычитания из уравнения (19) уравнение (20), находим эффективную молярную массу воздуха:
(21)
Легко сообразить, что изменение массы воздуха в сосуде равно изменению массы сосуда до и после его откачивания.
Уравнение (19) можно также использовать для нахождения плотности воздуха в комнате. Так как плотность вещества равна отношению его массы к объему, т.е. 
, то из (19) получаем:
(22)
VI. Приборы и принадлежности.
Для выполнения работы используется: 
1. Барометр для измерения атмосферного давления 
и термометр для измерения температуры воздуха T.
2. Весы для измерения массы 
откаченного из сосуда воздуха.
3.Установка для откачивания воздуха из сосуда и измерения остаточного давления в нем 
.
VII. Ход работы.
1. Провести необходимые измерения 5 раз и найти среднее значение молярной массы воздуха по формуле (21).
2. Рассчитать величину 
воздуха, считая его смесью газов. Принять молярную концентрацию азота в воздухе равной 78%, кислорода-21%, аргона-1%, долей остальных газов пренебречь. Сопоставить расчетное и экспериментальное значение
3. Используя найденные значения , рассчитать плотность воздуха в лаборатории.
VIII. Контрольные вопросы:
1. Вывести уравнение Клапейрона-Менделеева.
2. Что является основным достижением молекулярно-кинетической теории идеального газа? Физический смысл постоянной Больцмана? Газовые процессы.
3. Что такое молярная масса? Чему равен 1 моль газа? Как найти молярную массу смеси газов?
IX. Литература
Сивухин Д.В. Общий курс физики Т 2 . М: Наука,1979.
Матвеев А.Н. Молекулярная физика. М: Высшая школа, 1986.
Савельев И.В. Курс общей физики.Т2 Молекулярная физика. М: Наука 1982.
Стрелков С.П.Т2 Молекулярная физика. М: Наука 1975
Кикоин А.К., Кикоин И.К. Молекулярная физика. М: Наука. 1976.