Диаграммы деформирования и теории прочности для хрупких и пластичных материалов. Основные механические характеристики материалов.

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

 

Обобщенный закон Гука. Связь между нормальными и касательными напряжениями и деформациями. Коэффициент Пуассона.

Теория прочности Мора. Определение нормальных и касательных напряжений по кругам Мора.

Диаграммы деформирования и теории прочности для хрупких и пластичных материалов. Основные механические характеристики материалов.

В зависимости от характера разрушениям материалы разделяют на пластические или хрупкие.

Пластическое разрушение происходит путем сдвига частиц материала в плоскостях действия наибольших касательных напряжений. При этом в результате сдвига увеличивается длина образца.

При хрупком разрушении частицы материалы отрываются внезапно и плоскости поперечного сечения. В этом случае не наблюдается образование шейки, отсутствуют явления текучести и упрочнения материала.

Пластичные материалы разрушаются при больших остаточных деформациях ( ). Хрупкими называют материалы, разрушающиеся при малых остаточных деформациях, не превышающих 1-5%.

При испытании разные материалы обнаруживают различное поведение при нагружении, в соответствии, с чем все материалы делятся на две группы: пластические и хрупкие.

Диаграммы пластичного материала при испытании на растяжение и сжатие представлен на рис.1, диаграммы хрупкого материала (см. рис.2).

Пластичные материалы на диаграмме растяжения часто имеют характерный , называемый площадкой текучести, ему соответствует напряжения- предел текучести 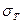. Явление текучести сопровождается образованием больших пластических, остаточных деформаций. Появление таких деформаций в элементах конструкции, как правило, приводит к нарушениям в работе конструкции, и являются нежелательными.

Хрупкие материалы выдерживают напряжения равные пределу прочности 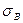и разрушаются без образования заметных остаточных деформаций. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, стекло, кирпич, строительные камни и др. Для таких материалов величина удлинения при разрыве 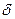не превышает 2-5%, а в ряде случаев измеряется долями процента.

4. Дифференциальное уравнение оси изогнутой балки. Определение изгибающего момента, поперечной силы и прогиба балки.