Критические области. Мощность критерия. Построение статистического критерия. Принцип отношения правдоподобия.

Критические точки – точки, которые находятся из табл по f(k) и α, разделяющие область на 2 или 3 части в зависимости от Н1.

Критические области – совокупность знач к, при которых отвергается Н₀. где

1 – область малых знач, 2- правдоподобных Знач. 3 – область больших значений

Мощность критерия – вероятность того, что принимается Н₁, если она верна, а Н₀ отвергается.

Мощность критерия = 1-β , где β – вероятность совершить ош 2 рода.

Чем ↑(1-β) , тем ↓β

 

Принцип отношения правдоподобия.

Требуется опр какому з-ну расредел принадлежат числа а,b,c - ?

Пусть з-н распредел Х(x) , Y(х) – нормальный.

У них отличаются ток мат ожидания.

Пусть Н0 : f(x)=X(x)

H1 : f(x) = Y(x)

Из рис => Н0 не противоречит экспериментальным данным, кажется правдоподобнее, чем Y(х).

 

К= чем ↓к , тем ↑ правдоподобие набл х1…хн в док-ве справедливости Н0.

Представление о сраведливости правдоподобностей имеющихся наблюдений х₁…х_n в отношении проверяемой Н₀ и альтернативн Н₁ гипотез дает сопоставление соотв ф-ций правдоподобия.

13. Проверка гипотезы о = центров распред 2х норм генеральных совокупностей при известном s.

Пусть 2 cлуч величины X и Y подчиняются НЗ они имеют 2 независимые выборки объемом n и m

1)Выдвигаем Но и Н1

Но: М(Х)=М(У)

Н1: М(Х)≠М(У)

2)

 

 

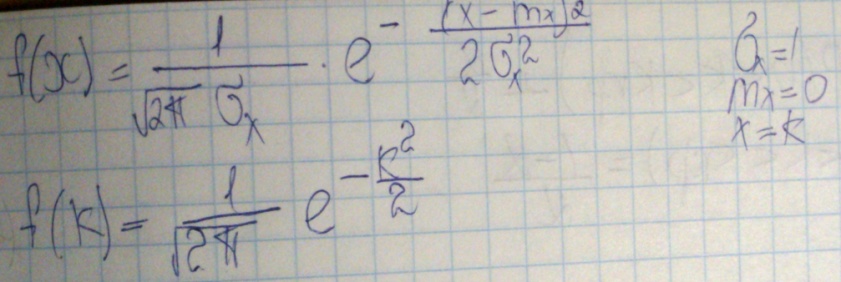
3)Задаем сл вел-ной ур-ия значимости λ

λ=P(|k|>kкр)

P(0<k<+ )=1/2

значит ½=р(0<k<kлз)+з(kкр<k<+ )

 

½= Ф(kкр)+λ/2 или Ф(kкр)=(1-λ)/2

Кнабл=