Интервальное оценивание. Доверительные интервал и вероятность. Распределение Стъюдента.

Интегральная оценка – оценка, определяется 2мя числами - концами интервала. Позволяет установить точность и надежность оценки.

Точность оценки∆ : |θ* - θ| < ∆ , ∆>0. Чем ↓∆ , тем точнее оценка.

Надежность оценка γ - вероятность, с которой осуществляется |θ* - θ| < ∆. Обычно надежность задается наперед (например: γ = 0,95 ; γ =0,99). γ = Р [θ* - ∆< θ < θ* + ∆]вероятность того, что интервал (θ*-∆; θ*+∆) заключает в себе (покрывает) неищв параметр θ равно γ.

Доверительный интервал I_β- интервал (θ*-∆; θ*+∆) , покрывающий неизв параметр θ с заданной надежностью γ. Доверительный интервал это СВ, т.к. она опр по выборке х₁…з_n

Доверительная надежность β – вероятность, с которой интервал накрывает θ. (надежность).

Β = Р (|θ* - θ| < ∆) β=∫ f(θ*) dθ*

Ширина β зависит от n (объема выборки) ∆à 0 при nà ∞ ; βà 1 при ∆ à ∞ . интервальное оценивание используется при небольших n.

Распределение Стъюдента.

СВ - Х распределена по НЗР, выборка х₁…х_n – СВ => их линейная комбинация тоже СВ Хв= * ∑х

М(Х_в) = * ∑М(Х) = Мх

D(Х_в) = 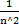D [∑M(X)] = 1/n² * n * Dx = Dx/n

Сформулируем величину

Если σ известно = M[(x_в-m_x)/(σ_x/n)] => σ_x->S => (x̅_в-m_x/S)* =t

 

9. Понятие о распределении Пирсона. (хи²)

Р-м Х_i = Х₁.Х_n - нормальные независимые СВ

М(Х_i) = 0 M(Х₁)=М(Х₂)= …. = М(Х_n) = 0

D(Х_i) =1 D(X₁)=D(X₂)= …. = D (X₂) =1

Тогда хи² = ∑Хi² хи² = Х₁² +…+Х_n² с к=n степенями свободы. (есди ∑х =nX то к=n-1 )

Распределение Пирсона – это плотность распределения СВ хи²

Зависит только от объема выборки n. n à ∞ тогода хи² à к НЗР

М(хи²)=n

D(хи²)=2n

S² = 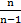* ∑[(Х_в-X_i)²/n] M[Х_в-X_i] = М_х-М_х = 0

Хи² = S² (n-1) / σ_x²