Предел и непрерывность функций двух переменных

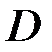Опр.Точка называется предельной точкой множества , если в любой ее окрестности содержатся точки множества 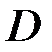, отличные от .

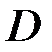Пусть функция определена в области и – предельная точка множества .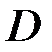

Опр. Число называют пределом функции при стремлении точки к точке , если для любого числа существует такое число , что выполняется неравенство как только .

.

Для существования предела функции при требуется, чтобы при любом способе стремления к существовал предел функции , и он был равен одному и тому же числу.

Пример 1. Показать, что существует предел функции в точке .

, . Следовательно, искомый предел существует и равен единице.

Пример 2. Показать, что для функции не существует предел в точке .

, данный предел не существует.

Все основные теоремы о пределах и правила их вычисления для функций одной переменной переносятся на случай функций нескольких переменных.

Опр. Полным приращением функции в точке называется разность , где и – приращения аргументов.

Опр. Функция называется непрерывной в точке , если она определена в некоторой окрестности этой точки и бесконечно малым приращениям аргументов и соответствует бесконечно малое приращение функции : .

Опр. Функция называется непрерывной в точке , если она определена в некоторой окрестности этой точки и .

Опр. Функция называется непрерывной в некоторой области, если она непрерывна в каждой точке этой области.

Опр. Если в некоторой точке функция не является непрерывной, то она называется разрывной в этой точке, а сама точка – точкой разрыва функции.

Точки разрыва функции двух переменных могут образовывать целые линии.