Понятие функции нескольких переменных
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Примеры функций нескольких переменных:
1. Площадь прямоугольника  является функцией двух независимых переменных – сторон прямоугольника
является функцией двух независимых переменных – сторон прямоугольника  и
и  :
:  .
.
2. Объем прямоугольного параллелепипеда  является функцией трех независимых переменных
является функцией трех независимых переменных  :
:  , где
, где  – ребра.
– ребра.
3. Работа электрического тока  на участке цепи зависит от разности потенциалов
на участке цепи зависит от разности потенциалов  на концах участка, силы тока
на концах участка, силы тока  и времени
и времени  :
:  .
.
Рассмотрим на плоскости  некоторое множество точек
некоторое множество точек 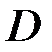 .
.
Опр. Величина  называется функцией двух переменных величин
называется функцией двух переменных величин  и
и  на множестве
на множестве 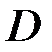 , если каждой точке этого множества соответствует одно определенное значение величины
, если каждой точке этого множества соответствует одно определенное значение величины  .
.
Множество 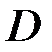 называется областью определения, а множество
называется областью определения, а множество  – областью значений функции
– областью значений функции 
 .
.
Пример. Найти область определения и область значений функций: 1)  ; 2)
; 2)  .
.
 1)
1)  ,
,  .
.
2) 
 ,
,  .
. 
Графиком функции двух переменных  является некоторая поверхность в пространстве ℝ
является некоторая поверхность в пространстве ℝ  .
.
Функцию двух переменных можно задать аналитически, таблицей, графически.
Опр. Величина  называется функцией
называется функцией  переменных величин
переменных величин  , если каждой рассматриваемой совокупности этих величин соответствует одно определенное значение величины
, если каждой рассматриваемой совокупности этих величин соответствует одно определенное значение величины  :
:  .
.
Опр. Линией уровня функции  называется линия на плоскости
называется линия на плоскости  , в точках которой функция сохраняет постоянное значение.
, в точках которой функция сохраняет постоянное значение.
Опр. Сетью линий уровня функции  называется совокупность линий уровня, соответствующих различным
называется совокупность линий уровня, соответствующих различным  .
.
 Пример.
Пример.
 Для функции
Для функции  , графиком которой является параболоид вращения, равномерной сетью линий уровня служит система концентрических окружностей с центром в точке
, графиком которой является параболоид вращения, равномерной сетью линий уровня служит система концентрических окружностей с центром в точке  и сама эта точка.
и сама эта точка. 