Сведение нахождения оптимальных смешанных стратегий игроков к задаче линейного программирования.

Обозначим . Из определения нижней цены игры следует, что - наибольшее из тех чисел , для которых есть хотя бы один допустимый набор удовлетворяющий неравенствам

Будем считать, что все элементы платежной матрицы неотрицательны (для этого их достаточно увеличить на одно и то же положительное число, оптимальные стратегии при этом не изменятся). Поделим все неравенства системы на и обозначим . Тогда, с учетом соотношения , получаем . Таким образом, задача по определению смешанных стратегий первого игрока сводится к следующей задаче линейного программирования.

,

.

Если есть решение задачи, то цена игры равна , а оптимальная стратегия игрока определяется из соотношений .

Несколько более удобно решать задачу по определению верхней цены игры и максиминной стратегии второго игрока. По определению нижней цены получаем, что есть наименьшее значение из тех , для которых выполняются неравенства

хотя бы для одного допустимого набора . Обозначая , получаем следующую задачу линейного программирования

,

.

Если решение задачи, то , .

Задачи по определению максиминной стратегии перового игрока и минимаксной стратегии второго игрока являются двойственными по отношению друг к другу, поэтому, решив одну из задач, из соответствующей симплекс таблицы мы можем одновременно определить решение второй задачи.

 

Задача 6.4. Рассматривается антагонистическая игра двух лиц с нулевой суммой и платежной матрицей (первый игрок - получатель платежа, - выбирает строку платежной матрицы, второй - плательщик, - выбирает столбец). Требуется: 1) определить верхнюю и нижнюю цену игры в чистых стратегиях; 2) найти цену игры и оптимальные смешанные стратегии игроков графическим способом; 3) свести нахождение смешанных стратегий второго игрока к задаче линейного программирования и найти цену игры.

Решение. Найдем сначала верхнюю и нижнюю цену игры в чистых стратегиях. Для нахождения верхней цены (привелигирован первый игрок) подчеркнем максимум в каждом из столбцов платежной матрицы, а затем выберем наименьшее значение из этих максимумов.

Следовательно, , а минимаксной стратегией второго игрока является либо первая, либо третья. Для нахождения нижней цены игры подчеркнем наименьшее значение из чисел платежной матрицы в каждой строке и выберем наибольшее из этих минимумов.

Следовательно, , а максиминной стратегией первого игрока является любая из двух, первая или вторая. Поскольку , цены игры и решения в чистых стратегиях нет.

Найдем оптимальные смешанные стратегии игроков и цену игры графическим способом. Для этого нам надо построить графики четырех функций

,

,

,

,

на отрезке , определить

,

а затем найти .

 

 

(4) 16

 

 

11 (2)

9 (1) 9

 

7 7

 

2 (3) 2

 

 

0 1

Из рисунка видно, что точка максимина соответствует пересечению графиков второй и третьей функции, то есть

,

откуда

Û , .

Для определения смешанной стратегии второго игрока следует решить уравнение

,

откуда

, .

Таким образом, оптимальные стратегии игроков определены однозначно - это стратегия для первого игрока, и стратегия для второго. Цена игры в смешанных стратегиях равна .

Сведем теперь задачу нахождения оптимальной стратегии второго игрока задаче линейного программирования. Получаем:

 

,

, .

 

Приведем задачу к стандартной форме

 

 

Запишем условия задачи в виде симплекс-таблицы.

 

Б
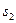
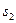
	-1	-1	-1	-1

Ö

 

 

Б

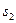
Ö

 

Б

 

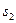
Найдено следующее решение задачи линейного программирования:

, , , .

Переходя к вероятностям, получим

, , .

Одновременно мы нашли решение двойственной задачи: оптимальные значения двойственных переменных , содержатся в -строке в столбцах, отвечающих вспомогательным переменным и 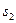соответственно. Таким образом, , , . Окончательно, , . Ответы совпали с ответами, полученными графическим способом.