Формула Тейлора для функции нескольких переменных.

Как известно, функцию F(t) при условии существования ее производных по порядок n+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа (см. формулы (21.7), (21.11) первой части курса). Запишем эту формулу в дифференциальной форме:

(4.3)

где

В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.

Рассмотрим функцию двух переменных f(x, y), имеющую в окрестности точки (х₀ , у₀) непрерывные производные по (n + 1)-й порядок включительно. Зададим аргументам х и у некоторые приращения Δх и Δу и рассмотрим новую независимую переменную t:

(0 ≤ t ≤1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х₀ , у₀) и (х₀ + Δх, у₀ + Δу). Тогда вместо приращения Δf (x₀ ,y₀) можно рассматривать приращение вспомогательной функции

F(t) = f (x₀ + t Δx, y₀ + tΔy) , (4.4)

равное ΔF (0) = F (1) – F (0). Но F (t) является функцией одной переменной t, следовательно, к ней применима формула (4.3). Получаем:

.

Отметим, что при линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть

Подставив эти выражения в (4.3), получим формулу Тейлора для функции двух переменных:

, (4.5)

где 0<θ<1.

Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:

 

7. Необходимое условие экстремума. Достаточное условие экстремума.

Определение 5.1. Точка М₀ (х₀ , у₀ ) называется точкой максимума функции z = f (x, y), если f (x_o , y_o) > f (x, y) для всех точек (х, у) из некоторой окрестности точки М₀.

Определение 5.2. Точка М₀ (х₀ , у₀ ) называется точкой минимума функции z = f (x, y), если f (x_o , y_o) < f (x, y) для всех точек (х, у) из некоторой окрестности точки М₀.

 

Замечание 1. Точки максимума и минимума называются точками экстремумафункции нескольких переменных.

Замечание 2. Аналогичным образом определяется точка экстремума для функции от любого количества переменных.

 

Теорема 5.1 (необходимые условия экстремума). Если М₀ (х₀ , у₀ ) – точка экстремума функции z = f (x, y), то в этой точке частные производные первого порядка данной функции равны нулю или не существуют.

Доказательство.

Зафиксируем значение переменной у, считая у = у₀. Тогда функция f (x, y₀) будет функцией одной переменной х, для которой х = х₀ является точкой экстремума. Следовательно, по теореме Ферма или не существует. Аналогично доказывается такое же утверждение для .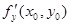

 

Определение 5.3. Точки, принадлежащие области определения функции нескольких переменных, в которых частные производные функции равны нулю или не существуют, называются стационарными точками этой функции.

 

Замечание. Таким образом, экстремум может достигаться только в стационарных точках, но не обязательно он наблюдается в каждой из них.

Примеры.

1. Найдем стационарную точку функции z = x² + y². Для этого решим систему уравнений откуда х₀ = у₀ = 0. Очевидно, что в этой точке функция имеет минимум, так как при х = у = 0 z = 0, а при остальных значениях аргументов z > 0.
2. Для функции z = xy стационарной точкой тоже является (0, 0), но экстремум в этой точке не достигается ( z (0, 0) = 0, а в окрестности стационарной точки функция принимает как положительные, так и отрицательные значения).

 

Теорема 5.2 (достаточные условия экстремума). Пусть в некоторой окрестности точки М₀ (х₀ , у₀ ) , являющейся стационарной точкой функции z = f (x, y), эта функция имеет непрерывные частные производные до 3-го порядка включительно. Обозначим Тогда:

1) f (x, y) имеет в точке М₀ максимум, если AC – B² > 0, A < 0;

2) f (x, y) имеет в точке М₀ минимум, если AC – B² > 0, A > 0;

3) экстремум в критической точке отсутствует, если AC – B² < 0;

4) если AC – B² = 0, необходимо дополнительное исследование.

Доказательство.

Напишем формулу Тейлора второго порядка для функции f (x, y), помня о том, что в стационарной точке частные производные первого порядка равны нулю:

где Если угол между отрезком М₀М , где М (х₀+Δх, у₀+Δу), и осью Ох обозначить φ, то Δх = Δρ cosφ, Δy = Δρsinφ. При этом формула Тейлора примет вид: . Пусть Тогда можно разделить и умножить выражение в скобках на А. Получим:

. (5.1)

Рассмотрим теперь четыре возможных случая:

1) AC-B² > 0, A < 0. Тогда , и при достаточно малых Δρ. Следовательно, в некоторой окрестности М₀ f (x₀ + Δx, y₀ + Δy) < f (x₀ , y₀), то есть М₀ – точка максимума.

2) Пусть AC – B² > 0, A > 0. Тогда , и М₀ – точка минимума.

3) Пусть AC-B² < 0, A > 0. Рассмотрим приращение аргументов вдоль луча φ = 0. Тогда из (5.1) следует, что , то есть при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча такого, что tg φ₀ = -A/B, то , следовательно, при движении вдоль этого луча функция убывает. Значит, точка М₀ не является точкой экстремума.

3`) При AC – B² < 0, A < 0 доказательство отсутствия экстремума проводится

аналогично предыдущему.

3``) Если AC – B² < 0, A = 0, то . При этом . Тогда при достаточно малых φ выражение 2B cosφ + C sinφ близко к 2В, то есть сохраняет постоянный знак, а sinφ меняет знак в окрестности точки М₀ . Значит, приращение функции меняет знак в окрестности стационарной точки, которая поэтому не является точкой экстремума.

4) Если AC – B² = 0, а , , то есть знак приращения определяется знаком 2α₀. При этом для выяснения вопроса о существовании экстремума необходимо дальнейшее исследование.

Пример. Найдем точки экстремума функции z = x² - 2xy + 2y² + 2x. Для поиска стационарных точек решим систему . Итак, стационарная точка (-2,-1). При этом А = 2, В = -2, С = 4. Тогда AC – B² = 4 > 0, следовательно, в стационарной точке достигается экстремум, а именно минимум (так как A > 0).