Частные производные.

 

Рассмотрим изменение функции 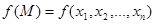при задании приращения только одному из ее аргументов – х_i , и назовем его .

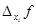Определение 1.7. Частной производной функции 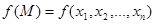по аргументу х_i называется .

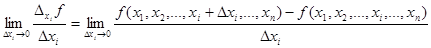Обозначения: .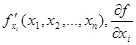

Таким образом, частная производная функции нескольких переменных определяется фактически как производная функции одной переменной – х_i. Поэтому для нее справедливы все свойства производных, доказанные для функции одной переменной.

Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными.

Примеры.

1. z = 2x² + 3xy –12y² + 5x – 4y +2,

2. z = x^y,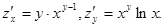

3.

 

Геометрическая интерпретация частных производных функции двух переменных.

 

Рассмотрим уравнение поверхности z = f (x,y) и проведем плоскость х = const. Выберем на линии пересечения плоскости с поверхностью точку М (х,у). Если задать аргументу у приращение Δу и рассмотреть точку Т на кривой с координатами (х, у+Δу, z+Δ_yz), то тангенс угла, образованного секущей МТ с положительным направлением оси Оу, будет равен 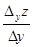. Переходя к пределу при 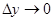, получим, что частная производная 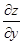равна тангенсу угла, образованного касательной к полученной кривой в точке М с положительным направлением оси Оу. Соответственно частная производная 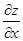равна тангенсу угла с осью Ох касательной к кривой, полученной в результате сечения поверхности z = f (x,y) плоскостью y = const.

Определение 2.1. Полным приращением функции u = f(x, y, z) называется

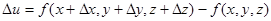
Определение 2.2. Если приращение функции u = f (x, y, z) в точке (x₀ , y₀ , z₀) можно представить в виде (2.3), (2.4), то функция называется дифференцируемой в этой точке, а выражение - главной линейной частью приращения или полным дифференциалом рассматриваемой функции.

Обозначения: du, df (x₀ , y₀ , z₀).

Так же, как в случае функции одной переменной, дифференциалами независимых переменных считаются их произвольные приращения, поэтому

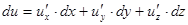
Замечание 1. Итак, утверждение «функция дифференцируема» не равнозначно утверждению «функция имеет частные производные» - для дифференцируемости требуется еще и непрерывность этих производных в рассматриваемой точке.

Замечание 2. Если в формуле (2.5) считать , и частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов

 

 

4. Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала.

Пусть функция z = f (x, y) является дифференцируемой в окрестности точки М (х₀ , у₀). Тогда ее частные производные 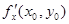и 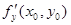являются угловыми коэффициентами касательных к линиям пересечения поверхности z = f (x, y) с плоскостями у = у₀ и х = х₀, которые будут касательными и к самой поверхности z = f (x, y). Составим уравнение плоскости, проходящей через эти прямые. Направляющие векторы касательных имеют вид {1; 0; 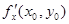} и {0; 1; 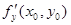}, поэтому нормаль к плоскости можно представить в виде их векторного произведения: n = {- 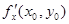,- , 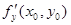1}. Следовательно, уравнение плоскости можно записать так:

, (4.1)

где z₀ = .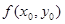

 

Определение 4.1. Плоскость, определяемая уравнением (4.1), называется касательной плоскостьюк графику функции z = f (x, y) в точке с координатами ( х₀ , у₀ , z₀ ).

 

Из формулы (2.3) для случая двух переменных следует, что приращение функции f в окрестности точки М можно представить в виде:

или

 

(4.2)

Следовательно, разность между аппликатами графика функции и касательной плоскости является бесконечно малой более высокого порядка, чем ρ, при ρ→0.

При этом дифференциал функции f имеет вид:

,

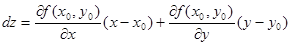что соответствует приращению аппликаты касательной плоскости к графику функции. В этом состоит геометрический смысл дифференциала.

 

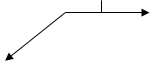
Определение 4.2. Ненулевой вектор, перпендикулярный касательной плоскости в точке М (х₀ , у₀) поверхности z = f (x, y), называется нормалью к поверхности в этой точке.

 

В качестве нормали к рассматриваемой поверхности удобно принять вектор --n = { 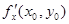, ,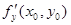-1}.

z

z = f (x,y)

M₀ (x₀ , y₀ , z₀)

n

y

M (x₀ , y₀)

x

Пример.

Составим уравнение касательной плоскости к поверхности z = xy в точке М (1; 1). При х₀ = у₀ = 1 z₀ =1; . Следовательно, касательная плоскость задается уравнением: z = 1 + (x – 1) + (y – 1), или x + y – z – 1 = 0. При этом вектор нормали в данной точке поверхности имеет вид: n = {1; 1; -1}.

Найдем приращение аппликат графика функции и касательной плоскости при переходе от точки М к точке N(1,01; 1,01).

Δz = 1,01² - 1 = 0,0201; Δz_кас = (1,01 + 1,01 – 1) – (1 + 1 – 1) = 0,02. Следовательно,

dz = Δz_кас = 0,02. При этом Δz – dz = 0,0001.

 

5. Производная по направлению.

 

Пусть функция u = f (x, y, z) непрерывна в некоторой области D и имеет в этой области непрерывные частные производные. Выберем в рассматриваемой области точку M(x,y,z) и проведем из нее вектор S, направляющие косинусы которого cosα, cosβ, cosγ. На векторе S на расстоянии Δs от его начала найдем точку М₁(х+Δх, у+Δу, z+Δz), где

Представим полное приращение функции f в виде:

где

После деления на Δs получаем:

.

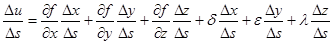Поскольку 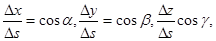предыдущее равенство можно переписать в виде:

 

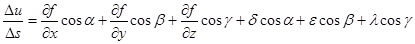(4.6)

Определение 4.3. Предел отношения 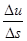при 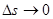называется производной от функции u = f (x, y, z) по направлению вектора Sи обозначается .

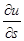При этом из (4.6) получаем:

(4.7)

 

Замечание 1. Частные производные являются частным случаем производной по направлению. Например, при получаем:

.

 

Замечание 2. Выше определялся геометрический смысл частных производных функции двух переменных как угловых коэффициентов касательных к линиям пересечения поверхности, являющейся графиком функции, с плоскостями х = х₀ и у = у₀. Аналогичным образом можно рассматривать производную этой функции по направлению l в точке М(х₀ , у₀) как угловой коэффициент линии пересечения данной поверхности и плоскости, проходящей через точку М параллельно оси Oz и прямой l.

Определение 4.4. Вектор, координатами которого в каждой точке некоторой области являются частные производные функции u = f (x, y, z) в этой точке, называется градиентомфункции u = f (x, y, z).

Обозначение: grad u = .

Свойства градиента.

1. Производная 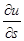по направлению некоторого вектора Sравняется проекции вектора grad u на вектор S. Доказательство. Единичный вектор направления S имеет вид e_S ={cosα, cosβ, cosγ}, поэтому правая часть формулы (4.7) представляет собой скалярное произведение векторов grad u и e_s, то есть указанную проекцию.

2. Производная в данной точке по направлению вектора S имеет наибольшее значение, равное |grad u |, если это направление совпадает с направлением градиента. Доказательство. Обозначим угол между векторами Sи grad u через φ. Тогда из свойства 1 следует, что |grad u |∙cosφ, (4.8) следовательно, ее наибольшее значение достигается при φ=0 и равно |grad u |.

3. Производная по направлению вектора, перпендикулярного к вектору grad u , равна нулю.

Доказательство. В этом случае в формуле (4.8)

4. Если z = f (x,y) – функция двух переменных, то grad f = направлен перпендикулярно к линии уровня f (x,y) = c, проходящей через данную точку.

6. Формула Тейлора для функции нескольких переменных. Производные и дифференциалы высших порядков

Частные производные функции z = f (x,y) являются, в свою очередь, функциями переменных х и у. Следовательно, можно найти их частные производные по этим переменным. Обозначим их так:

Таким образом, получены четыре частные производные 2-го порядка. Каждую из них можно вновь продифференцировать по х и по у и получить восемь частных производных 3-го порядка и т.д. Определим производные высших порядков так:

 

Определение 3.2. Частной производной n-го порядкафункции нескольких переменных называется первая производная от производной (n – 1)-го порядка.

 

Частные производные обладают важным свойством: результат дифференцирования не зависит от порядка дифференцирования (например, ). Докажем это утверждение.

Теорема 3.3. Если функция z = f (x,y) и ее частные производные определены и непрерывны в точке М (х, у) и в некоторой ее окрестности, то в этой точке

(3.3)

Доказательство.

Рассмотрим выражение и введем вспомогательную функцию . Тогда

. Из условия теоремы следует, что дифференцируема на отрезке [x, x+Δx], поэтому к ней можно применить теорему Лагранжа: где

[x, x+Δx]. Но Так как в окрестности точки М определена , дифференцируема на отрезке [y, y + Δy], поэтому к полученной разности вновь можно применить теорему Лагранжа: , где Тогда

Изменим порядок слагаемых в выражении для А:

и введем другую вспомогательную функцию , тогда Проведя те же преобразования, что и для , получим, что где . Следовательно,

. В силу непрерывности и . Поэтому, переходя к пределу при получаем, что , что и требовалось доказать.

Следствие. Указанное свойство справедливо для производных любого порядка и для функций от любого числа переменных.

 

Дифференциалы высших порядков.

 

Определение 3.2. Дифференциалом второго порядка функции u = f (x, y, z) называется

Аналогично можно определить дифференциалы 3-го и более высоких порядков:

 

Определение 3.3. Дифференциалом порядка k называется полный дифференциал от дифференциала порядка (k – 1): d ^k u = d (d ^k-1u).

 

Свойства дифференциалов высших порядков.

1. k-й дифференциал является однородным целым многочленом степени k относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные k-го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень):

.