Обработанных на настроенном станке
Лабораторная работа №1
Статистические исследования точности деталей,
обработанных на настроенном станке
ЦЕЛЬ РАБОТЫ
1. Овладеть методикой построения экспериментальной и теоретической кривых распределения размеров деталей, обработанных на настроенном станке.
2. Определить количество годных и бракованных деталей в исследуемой партии и вероятное количество годных и бракованных деталей, обрабатываемых на данном станке.
3. Дать оценку точности обработки на данном станке в сравнении с заданной точностью деталей.
ЗАДАНИЕ
На основе измерений размеров выборки из партии деталей выполнить статистический анализ точности обработки и оценить точность настройки станка на размер.
ИНСТРУМЕНТ, МАТЕРИАЛЫ И ОСНАСТКА
1. Партия обработанных деталей-колец в количестве 40 – 50 шт. (рис. 1).
 |
Рис. 1. Чертеж детали
2. Микрометр.
3. Стойка к микрометру.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Все погрешности, возникающие при механической обработке, могут быть сведены к следующим трем видам:
1. Систематические постоянные.
2. Систематические переменные.
3. Случайные.
Систематические постоянные погрешности – это такие, величина которых остается постоянной у каждой детали партии.
Причиной возникновения таких погрешностей являются, например, неточность настройки станка на заданный размер, погрешности станка и другие.
Систематические переменные погрешности также имеются у каждой детали партии, но их величина меняется по какой-либо закономерности. Источниками возникновения этих погрешностей могут быть, например, размерный износ инструмента, температурные деформации элементов технологической системы (станок – приспособление – инструмент – деталь) и др.
Случайные погрешности появляются в результате действия одного или нескольких факторов, величины которых сами подвержены колебаниям случайного характера. Источниками случайных погрешностей могут быть, например, колебания твердости и припусков у деталейданной партии.
С помощью методов математической статистики и теории вероятностей можно по результатам измерений части деталей (выборки) определить закон распределения размеров деталей сколь угодно большой партии (генеральной совокупности), обработанной на данном станке. Этот закон распределения будет учитывать величину и вероятность возникновения случайных погрешностей.
Многочисленными исследованиями показано, что в большинстве случаев распределение размеров деталей при обработкеих на настроенном станке происходит по закону нормального распределения случайных величин (закон Гаусса). Кривая нормального распределения описывается уравнением, которое будет приведено ниже. Анализ параметров этогоуравнения позволяет оценивать точность обработки деталей, правильность настройки станка на размер, прогнозировать ожидаемую точность и возможный процент брака большого количества деталей по результатам измерений выборочной партии. Покажем это на примере.
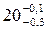 У детали задан наружный диаметр D = мм, взята выборка n = 50 штук. Результаты измерений деталей выборки приведены в табл. 1.
У детали задан наружный диаметр D = мм, взята выборка n = 50 штук. Результаты измерений деталей выборки приведены в табл. 1.
В эмпирических распределениях мерой рассеяния является размах. Размахом w’ называется разность между наибольшим xmax и наименьшим xmin измеренными значениями случайной величины:
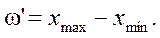 |
(1)
Таблица 1
Результаты измерений диаметра деталей-колец
| № п/п | D, мм | № п/п | D, мм | № п/п | D, мм | № п/п | D, мм | № п/п | D, мм |
| 19,81 | 19,82 | 19,82 | 19,85 | 19,83 | |||||
| 19,83 | 19,84 | 19,85 | 19,84 | 19,84 | |||||
| 19,84 | 19,84 | 19,84 | 19,85 | 19,85 | |||||
| 19,85 | 19,87 | 19,86 | 19,86 | 19,87 | |||||
| 19,86 | 19,88 | 19,88 | 19,87 | 19,89 | |||||
| 19,83 | 19,83 | 19,85 | 19,82 | 19,85 | |||||
| 19,84 | 19,84 | 19,84 | 19,83 | 19,84 | |||||
| 19,85 | 19,85 | 19,85 | 19,84 | 19,85 | |||||
| 19,86 | 19,86 | 19,86 | 19,85 | 19,86 | |||||
| 19,86 | 19,86 | 19,87 | 19,86 | 19,87 |
Размах делится не менее чем на 5 – 8 равных интервалов. Количество интервалов ориентировочно можно определить как k ≤ 5lg n. В каждый интервал включаются размеры, лежащие в пределах от наименьшего значения интервала включительно до наибольшего значения интервала, не включая его. Затем подсчитывается количество деталей в каждом интервале – частота mi.
Чтобы компенсировать погрешности измерения, величина интервала должна быть больше цены деления шкалы измерительного прибора, которым производится измерение величины x в выборке, не менее чем в два раза.
На основании данных (табл. 1) составлена таблица распределения размеров деталей, в которой приведены дополнительные графы для вычисления вспомогательных данных, упрощающих расчеты характеристик рассеивания (табл. 2).
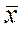 По полученным значениям можно найти среднее арифметическое значение размера (средний размер деталей в партии):
По полученным значениям можно найти среднее арифметическое значение размера (средний размер деталей в партии):
 |
, (2)
где xi — середина интервала, равная полусумме его граничных значений.
Длянаглядности по найденным результатам построим эмпирическую кривую распределения – полигон (рис. 2).
В координатной сетке по оси абсцисс отложим значения интерваловразмера x,а по оси ординат частоты mi, то есть количество деталей, попадающих в тот или иной интервал (табл.2). В результате построения получим фигуру, состоящую из вертикальных столбиков, которая называется гистограммой распределения случайной величины.
Таблица 2
Распределение диаметров деталей-колец
| Интервалы | Середина интервала, xi | Частота, mi | ximi | 
| xi – 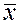
| (xi– 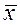 )2 )2
| (xi – 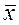 )2mi )2mi
| σ |
| 19,81–19,82 | 19,815 | 19,815 | 19,855 | – 0,040 | 0,0016 | 0,0016 | 0,017 | |
| 19,82–19,83 | 19,825 | 59,475 | – 0,030 | 0,0009 | 0,0027 | |||
| 19,83–19,84 | 19,835 | 99,175 | – 0,020 | 0,0004 | 0,0020 | |||
| 19,84–19,85 | 19,845 | 218,295 | – 0,010 | 0,0001 | 0,0011 | |||
| 19,85–19,86 | 19,855 | 238,26 | 0,000 | |||||
| 19,86–19,87 | 19,865 | 198,65 | 0,010 | 0,0001 | 0,0010 | |||
| 19,87–19,88 | 19,875 | 99,375 | 0,020 | 0,0004 | 0,0020 | |||
| 19,88–19,89 | 19,885 | 39,77 | 0,030 | 0,0009 | 0,0018 | |||
| 19,89–19,90 | 19,895 | 19,895 | 0,040 | 0,0016 | 0,0032 | |||
| ∑50 | ∑992,71 | ∑0,0154 |
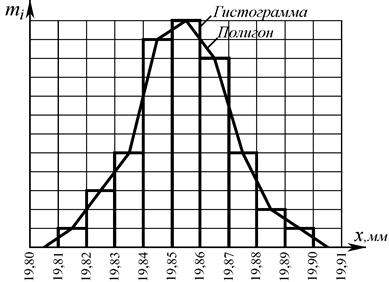 |
Рис. 2. График распределения случайной величины
Проведя ломаную линию через середины вершин столбиков, получим полигон распределения случайной величины.
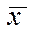 Из рис. 2 видно, что площади гистограммы и полигона равны. Рассмотренные ранее характеристики , ω’ не дают возможности оценить плотность группирования размеров деталей около значения , что очень важно для оценки качества технологического процесса и вероятности возникновения брака.
Из рис. 2 видно, что площади гистограммы и полигона равны. Рассмотренные ранее характеристики , ω’ не дают возможности оценить плотность группирования размеров деталей около значения , что очень важно для оценки качества технологического процесса и вероятности возникновения брака.
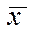
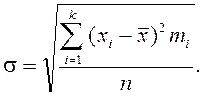 Характеристикой, которая может дать такую оценку, является среднее квадратическое отклонение от среднего значения – σ, которое вычисляется по следующей формуле:
Характеристикой, которая может дать такую оценку, является среднее квадратическое отклонение от среднего значения – σ, которое вычисляется по следующей формуле:
(3)
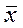 Величина среднего квадратического отклонения σ оценивает форму кривой распределения и фактически дает характеристику того, какие количества величин x и на каких расстояниях отстоят от величины . Размерность σ совпадает с размерностью случайной величины x (в нашем примере мм).
Величина среднего квадратического отклонения σ оценивает форму кривой распределения и фактически дает характеристику того, какие количества величин x и на каких расстояниях отстоят от величины . Размерность σ совпадает с размерностью случайной величины x (в нашем примере мм).
Для оценки генеральной совокупности по результатам оценки выборочной партии необходимо эмпирическую кривую распределения (полигон) заменить теоретической кривой. Как было указано, случайные величины имеют распределение, соответствующее закону Гаусса (рис. 3).
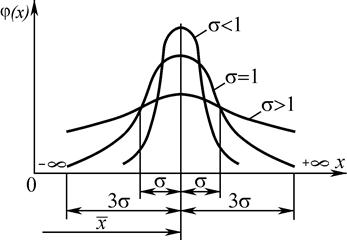 |
Рис. 3. Теоретическая кривая нормального распределения
В эмпирическом законе распределения взамен плотности вероятности j(x) используется частота mi. По смыслу эти понятия одинаковы, но mi используется для оценки выборки, а j(x) – для оценки генеральной совокупности.
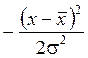
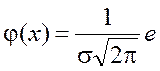 Уравнение кривой Гаусса:
Уравнение кривой Гаусса:
, (4)
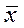 где x — переменная случайная величина; j(x) — плотность вероятности; σ — среднее квадратическое отклонение величин x и .
где x — переменная случайная величина; j(x) — плотность вероятности; σ — среднее квадратическое отклонение величин x и .
Кривая Гаусса обладает рядом свойств. Отметим главные из них.
1. Ветви кривой асимптотически приближаются к оси абсцисс, сливаясь с ней в бесконечности, то есть зона рассеивания случайной величины x лежит в пределах ± ∞.
2. 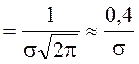
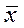 Максимальное значение величины j(x) будет при x = и соответственно составит:
Максимальное значение величины j(x) будет при x = и соответственно составит:
jmax .
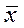 3. Значение величины j для значений x = ± σ составляет
3. Значение величины j для значений x = ± σ составляет
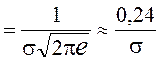 |
js .
 4. Кривая имеет перегибы, отстоящие на расстоянии ± σ от среднего значения .
4. Кривая имеет перегибы, отстоящие на расстоянии ± σ от среднего значения .
5. При увеличенииσ кривая «сплющивается», а при уменьшении «вытягивается» вверх (рис. 3).
6. Площадь под кривой нормального распределения может быть найдена путем интегрирования уравнения (4) и характеризует собой вероятность того, что случайная величина будет располагаться внутри интервала ± ∞. Совершенно очевидно, что в пределы ± ∞ попадут полностью все значения x. Поэтому вероятность попадания в этот интервал равна единице (достоверность).
 | |||
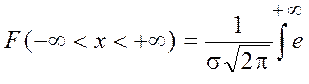 | |||
dx = 1.
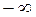 |
 7. Для практики достаточным являются пределы, равные не ± ∞,а ± 3σ от значения , так как в эти пределы попадает 99,73% всех значений случайной величины x. Практически
7. Для практики достаточным являются пределы, равные не ± ∞,а ± 3σ от значения , так как в эти пределы попадает 99,73% всех значений случайной величины x. Практически
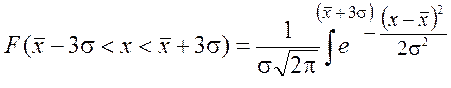 |
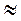 dx = 0,9973 1. (5)
dx = 0,9973 1. (5)
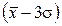 |
Вероятность значений величины x в любом другом интервале может быть найдена по аналогичной формуле

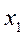 dx.
dx.
Произведя замену переменной x путем подстановки
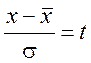 |
, (6)
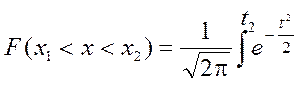 |
получим dt.
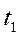 | |||
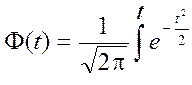 |
Интеграл dt
 |
 носит название нормированной функции Лапласа, и его значения для различных
носит название нормированной функции Лапласа, и его значения для различных
приведены в табл. 3.
Значение Ф(t) выражает отношение площади, соответствующей заданному интервалу{0 ; t} ко всей площади под кривой, которая равна единице.
 Введением переменной t начало отсчета величин x переносится в точку, соответствующую .
Введением переменной t начало отсчета величин x переносится в точку, соответствующую .
Для оценки генеральной совокупности по результатам оценки выборочной партии заменим эмпирическую кривую распределения теоретической кривой.
Прежде всего определим σ по формуле (3). Для подсчетаσ удобно воспользоваться табл. 2.
Построим на одном графике полигон распределения (был ранее построен на рис. 2) и теоретическую кривую распределения. При этом должно быть выдержано равенство площадей под кривыми. Для обеспечения этого требования ординаты теоретического распределения необходимо домножить на масштабный коэффициент, равный произведению величины интервала на число деталей в выборке ∆xn (площадь под эмпирической кривой).
Таблица 3
Значения функции Лапласа
| t | Ф(t) | t | Ф(t) |
| 0,0 | 0,0000 | 1,8 | 0,4641 |
| 0,1 | 0,0398 | 1,9 | 0,4713 |
| 0,2 | 0,0793 | 2,0 | 0,4772 |
| 0,3 | 0,1179 | 2,1 | 0,4821 |
| 0,4 | 0,1554 | 2,2 | 0,4861 |
| 0,5 | 0,1915 | 2,3 | 0,4893 |
| 0,6 | 0,2257 | 2,4 | 0,4918 |
| 0,7 | 0,2580 | 2,5 | 0,4938 |
| 0,8 | 0,2881 | 2,6 | 0,4953 |
| 0,9 | 0,3159 | 2,7 | 0.4965 |
| 1,0 | 0,3413 | 2,8 | 0,4974 |
| 1,1 | 0,3643 | 2,9 | 0,4981 |
| 1,2 | 0,3849 | 3,0 | 0,49865 |
| 1,3 | 0,4032 | 3,1 | 0,49903 |
| 1,4 | 0.4192 | 3,2 | 0,49931 |
| 1,5 | 0,4332 | 3,3 | 0,49952 |
| 1,6 | 0,4452 | 3,4 | 0,49966 |
| 1,7 | 0,4554 | 3,5 | 0,49977 |
С учетом этого ординаты теоретической кривой будут:
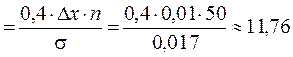 |
Ymax, (7)
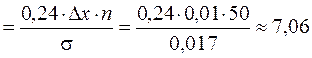 |
Ys. (8)
 Y3s .
Y3s .
Оценим точность изучаемой операции.
Для закона нормального распределения зона практического рассеивания w равна 6s.
Если выполняется неравенство
T ≥ 6s,
где T — допуск на размер детали (задается преподавателем), то точность операции считается достаточной.
Однако на практике возможен брак даже при достаточной точности процесса, если настройка станка была выполнена с погрешностью, величина которой превышала допустимое значение. Это видно из рис. 4.
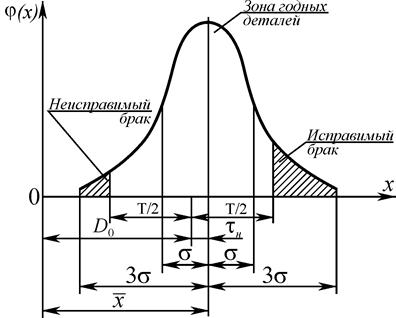 |
Рис. 4. Замена полигона распределения размеров теоретической кривой
Погрешность настройки определяем по формуле:
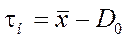 |
, (9)
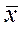 где tн – погрешность настройки или величина смещения центра распределения
где tн – погрешность настройки или величина смещения центра распределения
от координаты середины поля допуска D0.
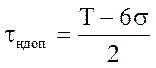 Допустимое значение погрешности настройки:
Допустимое значение погрешности настройки:
.
Для работы без брака должно соблюдаться условие
tн ≤ tндоп .
Если это условие выполняться не будет, неизбежен брак даже при избыточной точности процесса.
В рассматриваемом примере допуск на размер по чертежу детали составляет T = 0,2 мм, а s = 0,017 мм. Так как 6s < T, то точность процесса является хорошей и даже избыточной. Коэффициент точности процесса
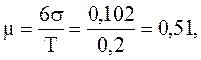 (10)
(10)
при μ ≤ 1 – точность процесса удовлетворительная; μ > 1 – точность процесса
неудовлетворительная.
Координата середины поля допуска
 |
.
Смещение центра рассеивания от координаты середины поля допуска
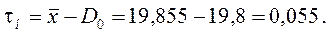
Коэффициент смещения настройки станка
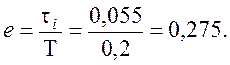 |
(11)
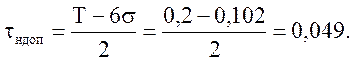 Допускаемое смещение центра рассеивания от координаты середины поля допуска
Допускаемое смещение центра рассеивания от координаты середины поля допуска
Допускаемая величина коэффициента смещения настройки станка
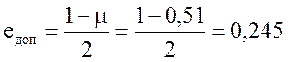 |
.
Так как tн > tндоп, e > eдоп, то при данной настройке станка возможен брак.
Процент исправимого и неисправимого брака определяется по формулам:
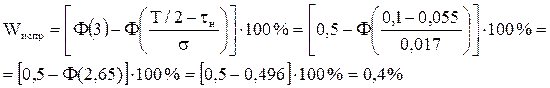 |
, (12)
 |
. (13)
Возможный процент годных деталей определяется по формуле:
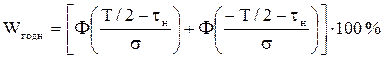 |
.
Из рассмотренного примера видно, что по полигону и по теоретической кривой распределения может быть установлен ожидаемый процент брака в генеральной совокупности деталей, достаточно полно охарактеризовано соответствие процесса предъявляемым точностным требованиям и оценена точность настройки станка, на котором обрабатывались детали.
ПРОВЕДЕНИЕ РАБОТЫ
1. Произвести измерение выборки из партии деталей. Результаты измерений внести в табл. 1.
2. Определить величину размаха ω’.
3. Разбить размеры на равные интервалы (количество интервалов 5 – 8 шт.) иподсчитать частоты, то есть количество деталей, попадающих в каждый интервал. Внести полученные данные в табл. 2.
4. По данным табл. 2 построить гистограмму и полигон.
5. 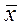 Определить значение по формуле (2) и значенияσ по формуле(3), используя для подсчетов табл. 2.
Определить значение по формуле (2) и значенияσ по формуле(3), используя для подсчетов табл. 2.
6. Найти значения Ymax , Ys с учетом масштабного коэффициента(∆x∙n) по формулам (7) и (8).
7. Построить совмещенную с гистограммой теоретическую кривую распределения по координатным точкам:
| x | x = 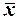
| x = σ | x = 3σ |
| Y | Ymax | Ys | Y = 0 |
8. Используя табл. 3, определить по формулам (12), (13) процент брака в генеральной совокупности.
9. Нанести на графике границы годных деталей и дать заключение о возможности исправления брака (исправимый или неисправимый брак).
10. Используя формулы (9), (10), (11), оценить точность обработки и правильность настройки станка, на котором были обработаны детали.
11. Оформить отчет.
ВОПРОСЫ К РАБОТЕ №1
1. Виды погрешностей обработки и основные причины их возникновения.
2. Для оценки каких погрешностей используется метод кривых распределения?
3. Как определяют размах и величину интервала?
4. Как строят гистограмму распределения и полигон?
5. Для чего устанавливают теоретический закон распределения размеров по данным измерений выборки деталей?
6. Как строится кривая Гаусса?
7. Какими свойствами характеризуется кривая Гаусса?
8. Как рассчитывают процент годных и бракованных деталей? Показать на графике зоны исправимого и неисправимого брака.
9. Как определить погрешность настройки станка? Показать на графике.
10. Как определить допустимую величину погрешности настройки станка?
11. Каким коэффициентом оценивается точность процесса обработки?