Модели портфельного инвестирования
Целью современной теории формирования и управления портфелем ценных бумаг является разработка методов, с помощью которых инвестор может выбрать оптимальный для себя портфель из бесконечного числа возможных.
Нынешнее состояние финансового рынка заставляет быстро и адекватно реагировать на его изменения, поэтому роль управления инвестиционным портфелем резко возрастает и заключается в нахождении той грани между ликвидностью, доходностью и рискованностью, которая позволила бы выбрать оптимальную структуру портфеля. Этой цели служат различные модели выбора оптимального портфеля.
Все методы формирования портфелей можно условно разбить на а) эмпирические и б) математически и статистически обоснованные. Второй способ более объективный и точный, но и более трудоёмкий. Получение математической оценки состояния портфеля на разных этапах инвестирования при учёте влияния различных факторов делает возможным непрерывно управлять структурой портфеля на каждом этапе принятия решения, то есть, по сути, управлять рисками.
Использование компьютерной реализации моделей значительно увеличивает оперативность получения аналитического материала для принятия решений. Следовательно, выполняются такие основные свойства управления как эффективность, непрерывность и оперативность.
В настоящее время существует множество моделей по формированию
портфеля ценных бумаг. Наиболее известной является модель Гарри Марковица и производная от неё модель Вильяма Шарпа.
Гарри Макс Марко́виц (англ. Harry Max Markowitz; род. 24 августа 1927, Чикаго) — выдающийся американский экономист (Калифорнийского университета в Сан-Диего Он окончил Чикагский университет, степень доктора получил там же; основоположник современной портфельной теории; известен пионерской работой, в которой предложил новый подход к исследованию эффектов риска распределения инвестиций, корреляции и диверсификации ожидаемых инвестиционных доходов; лауреат Нобелевской премии (1990) «за работы по теории финансовой экономики».
Уильям Форсайт Шарп (англ. William Forsyth Sharpe; род. 16 июня 1934, Бостон, Массачусетс) — американский экономист. Лауреат Нобелевской премии 1990 г. «за работы по теории финансовой экономики». Окончил Калифорнийский университет (Лос-Анджелес), степень доктора получил там же. Преподавал в университете штата Вашингтон, Калифорнийском и Стэнфордском университетах.
Согласно этой модели после определения ожидаемой доходности и дисперсии всех рассматриваемых ценных бумаг, а также после оценки их ковариации и установления безрисковой процентной ставки, инвестор составляет структуру «касательного» портфеля, а также ожидаемую доходность и среднеквадратическое отклонение. На следующем этапе выбирается оптимальный портфель, отмечая на графике те точки, где одна из кривых
безразличия касается, но не пересекает эффективное множество. И так как эффективное множество представляет собой прямую, то оптимальный портфель включает инвестиции в «касательный» портфель, комбинированный с определённым количеством безрисковых вложений и кредитов. Эта модель требует подробного рассмотрения, т.к. многие модели опираются на положения Гарри Марковица.
Подход Марковица может быть рассмотрен как дискретный подход, при котором начало периода обозначается t=0, а конец периода t=l. В момент t=0 инвестор должен принять решение о покупке конкретных ценных бумаг, это решение эквивалентно выбору оптимального портфеля из набора возможных портфелей.
Гарри Марковиц вводит понятия начального и конечного благосостояния. Доходность ценной бумаги за один период рассчитывается по формуле
Доходность =
Благосостояние в конце периода - Благосостояние в начале периода ,
Благосостояние в начале периода
где «Благосостоянием в начале периода» называется цена покупки одной ценной бумаги данного вида в момент t=0, а «благосостоянием в конце периода» называется рыночная стоимость данной ценной бумаги в момент t=l в сумме со всеми выплатами.
Аналогичным образом вычисляется доходность портфеля:
,
где W0 (W1)-совокупная рыночная стоимость всех ценных бумаг, входящих в портфель в момент t=0, t=l.
Марковиц утверждает, что инвестор должен основывать своё решение по выбору портфеля исключительно на ожидаемой доходности и стандартном отклонении, проводить эти расчёты для каждого портфеля, а затем выбрать «лучший» из них, основываясь на соотношении этих двух параметров. Каждый инвестор выбирает это соотношение в соответствии со своими целями. Для выбора наиболее желательного портфеля можно использовать так называемые кривые безразличия (рисунок 7.1).
| rв rc ra rD |
|
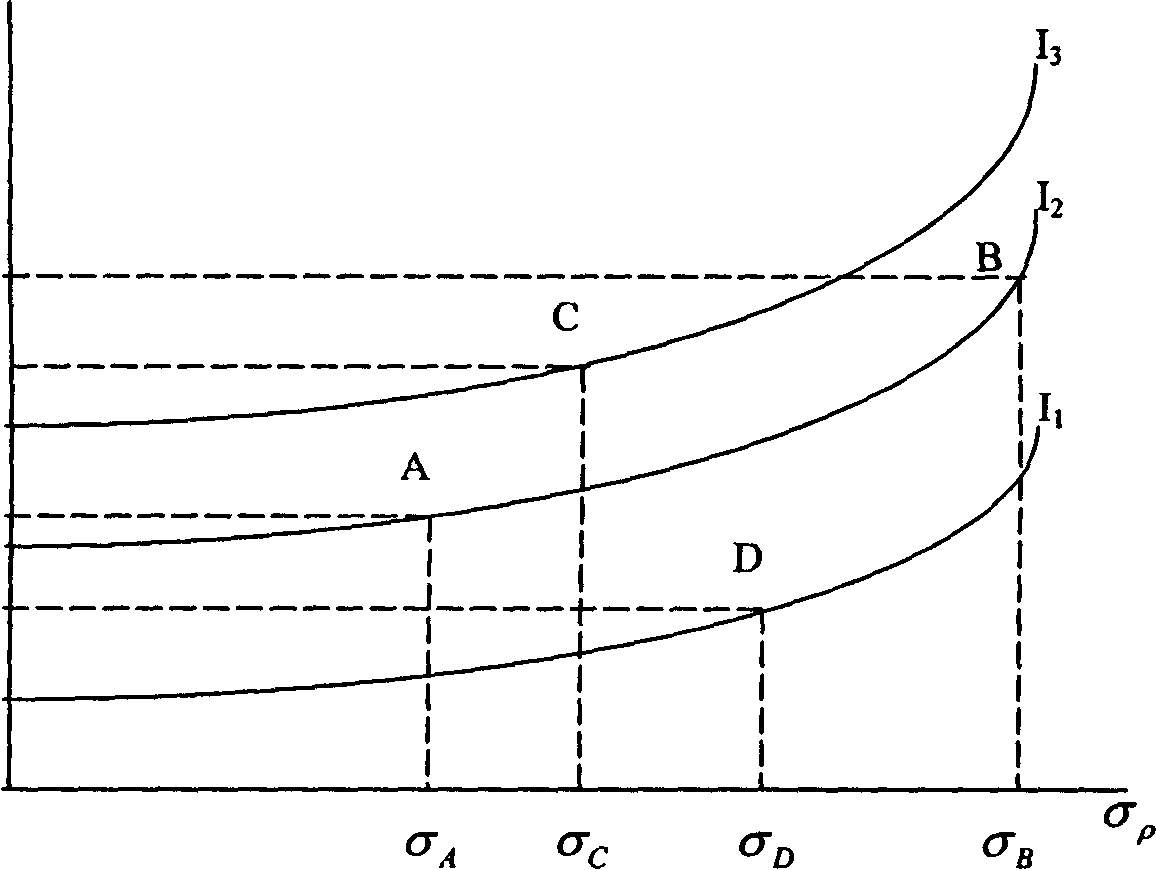
Рисунок 7.2- График кривых безразличия инвестора, избегающего
Риска
Рисунок 7.2 представляет собой график кривых безразличия гипотетического инвестора. Каждая кривая линия отображает одну кривую безразличия инвестора и представляет все комбинации портфелей, которые обеспечивают заданный уровень желаний инвестора. Это означает, что инвестор сочтёт портфели А и В равноценными, несмотря на то, что они имеют различные ожидаемые доходности и стандартные отклонения, так как оба этих портфеля лежат на одной кривой безразличия I2. С точки зрения получения максимальной доходности и минимизации риска он выберет портфель с больше ожидаемой доходностью, чем у портфеля А и стандартным отклонением
меньшим, чем у портфеля В. Это объясняется тем, что портфель С лежит на кривой безразличия I3, которая расположена выше и левее, чем I2.. Таким образом инвестор будет считать любой портфель, лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель, лежащий на кривой безразличия, которая находится ниже и правее. Следует заметить, что инвестор имеет бесконечное число кривых безразличия. Это означает, что, как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую лежащую между ними, как и из любого набора ценных бумаг можно сформировать бесконечное число портфелей. Однако, возникает вопрос, неужели необходимо проводить оценкувсех этих портфелей? В этом случае можно воспользоваться теоремой об эффективном множестве.
Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых:
1. Обеспечивает максимальную ожидаемую доходность для некоторого уровня риска.
2. Обеспечивает минимальный риск для некоторого значения ожидаемой доходности.
Набор портфелей, удостоверяющих этим двум условиям, называется эффективным множеством, или эффективной границей.
Рисунок 7.2 представляет иллюстрацию местоположения достижимого множества, также известного как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой портфели, которые могут быть сформированы из N ценных бумаг. Это означает, что все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества (точки G,E,S и Н на рисунке 7.3).
| S |
rp
| Достижимое множество |
| E |
| H |
S
| G |
sp
Рисунок 7.3- Достижимое и эффективное множество
Если посмотреть на рисунок 7.3 можно заметить, что не существует менее рискового портфеля, чем портфель Е, так как при проведении вертикальных прямых через точку Е ни одна точка достижимого множества не будет лежать левее данной прямой. Аналогично нет более рискованного портфеля чем портфель Н. Таким образом, множество портфелей, обеспечивают максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы достижимого множества, расположенного жду точками Е и Н. Также можно сказать, что не существует портфеля обеспечивающего большую доходность, чем портфель S и не существует портфеля, обеспечивающего меньшую доходность, чем портфель G. Таким образ множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы, достижимого множества, расположенная между точками S и G. В результате больший интерес представляют те портфели, которые лежат на верхней и левой границе достижимого множества между точками Е и S - это и есть множество эффективных портфелей. Все остальные портфели - неэффективные.
Для выбора оптимального портфеля инвестор должен нарисовать свои кривые безразличия на одном рисунке с эффективным множеством, а затем приступить к выбору портфеля, расположенного на кривой безразличия, находящегося выше и левее остальных. Этот портфель будет соответствовать точке, в которой кривая безразличия касается эффективного множества. Как это видно из рисунка 7.4 таким портфелем является портфель О* на кривой безразличия I2.
Как можно увидеть на рисунке 7.4 эффективное множество в общем случае вогнуто и имеет положительный наклон, то есть отрезок, соединяющий любые две точки эффективного множества, лежит ниже данного множества.
Это свойство эффективных множеств является очень важным, так как оно означает, что существует только одна точка касания эффективного множества и кривых безразличия.
Эффективное множество всегда является вогнутым и «впадин» на нем не существует. И считается, что оно не может иметь никакую другую форму, так как если бы была «впадина» допустим между точками Е и К (рисунок 7.4), то вложения допустим в портфель W не будет соответствовать оптимальному портфелю. Инвестор может вложить часть своих фондов в портфель Е, а оставшуюся в портфель К. Это вложение будет "более эффективным", так как они располагаются на рисунке левее рассматриваемого эффективного множества.
|
| I3 l2 I1 |
| S |
| H |
| G |
| E |
| O* |
| W |
| K |
sp
Рисунок 7.4 - Выбор оптимального портфеля
Для определения структуры портфеля отметим точку О*, расположенную на эффективном множестве модели Марковица. Она лежит между вторым и третьим ближайшими «угловыми» портфелями, обозначенными К и Е соответственно. Так как искомый портфель лежит между этими двумя «угловыми портфелями», то его структура является взвешенным средним структур К и Е. Веса этих портфелей можно определить графическим путем при проведении горизонтальной линий от точки О* до вертикальной оси, по которой измеряется доходность.
После того как были определены структура и местоположение эффективного множества Марковица, можно определить состав оптимального портфеля инвестора.
Если ожидаемая доходность оптимального портфеля обозначена, как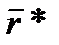 
и ожидаемые доходности двух ближайших «угловых» портфелей обозначены 
и 
соответственно, тогда состав оптимального портфеля может быть определён с помощью решения следующего уравнения относительно Y
.
Оптимальный портфель будет состоять из доли, инвестируемой в ближайший «угловой» портфель, находящийся «выше» оптимального, и доли (1-Y), инвестируемой в ближайший «угловой» портфель, расположенный ниже оптимального.
Оптимизация портфеля по Марковицу - это нахождение таких пропорций Xi, при формировании портфеля, которые при заданной cредней доходности портфеля 
минимизируют общий портфельный риск.
Итак, подход Марковица предполагает, что активы, предполагаемые для инвестиций, в отдельности являются рискованными, т.е. каждый из N рискованных активов даёт неопределённый доход за период владения. Поскольку никакой из активов не имеет совершенно отрицательной корреляции с любым другим активом, то все портфели дают неопределённые доходы за период владения и, следовательно, являются рискованными.
Кроме того, инвестору не позволяется использовать одолженные деньги вместе с начальным капиталом для покупки портфеля активов. Это означает, что инвестору не разрешается использовать финансовую поддержку или счёт, находящийся у его брокера, что несёт не только неудобство, но и снижение возможной доходности от операций.
Эти недостатки были устранены в обобщенных подходах Вильяма Шарпа.
Во-первых, инвестор получил возможность инвестировать не только в рискованные (X), но и в безрисковые активы (X - 1), а также одалживать деньги при обязательных выплатах по определённой процентной ставке по взятым займам.
С появлением на рынке безрискового актива инвестор получил возможность вкладывать часть своих денег в этот актив, а остаток - в любой из рискованных портфелей, содержащихся во множестве достижимости Марковица. Появление новых возможностей существенно расширяет множество достижимостии, что важнее,изменяет расположение значительной части эффективного множества Марковица.