Пирамидальная сортировка
Для сортировки массивов данных содержащих n элементов можно использовать класс пирамиды. Для этого необходимо, в начале, массив данных преобразовать в пирамиду, а затем удалить последовательно все элементы из пирамиды. Т.к. при очередном удалении в вершине пирамиды будет находиться минимальный элемент, то полученный массив будет отсортирован по возрастанию.
Для преобразования случайного массива данных в пирамиду можно воспользоваться для всех не листовых элементов методом MoveDown.
Пусть в массиве n элементов, тогда индекс последнего элемента будет 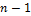 , а индекс его родителя
, а индекс его родителя 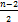 . Для всех узлов от 0 до
. Для всех узлов от 0 до 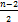 необходимо вызвать метод MoveDown. Реализовать данный алгоритм можно с помощью перегруженного конструктора класса THeap.
необходимо вызвать метод MoveDown. Реализовать данный алгоритм можно с помощью перегруженного конструктора класса THeap.
template <class T>
THeap<T>::THeap(vector<T> A)
{
Items=A;
FSize=A.size();
for (int i = (FSize-2)/2; i >= 0; i--)
MoveDown(i);
}
Алгоритм пирамидальной сортировки можно реализовать с помощью следующей функции:
template <class T>
void HeapSort(T *A, const int n)
{
vector<T> Vector;
for (int i = 0; i < n; i++)
Vector.push_back(A[i]);
THeap<T> Heap(Vector);
for (int i = 0; i < n; i++)
A[i]=Heap.Delete();
}
Анализ вычислительной сложности данного алгоритма показывает, что для преобразования массива в пирамиду потребуется  вызова метода MoveDown, внутри каждого из которых потребуется в наихудшем случае
вызова метода MoveDown, внутри каждого из которых потребуется в наихудшем случае 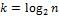 перестановок. При удалении элементов из пирамиды потребуется (n-1) вызовов метода MoveDown c
перестановок. При удалении элементов из пирамиды потребуется (n-1) вызовов метода MoveDown c 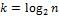 перестановками в наихудшем случае. Общие затраты:
перестановками в наихудшем случае. Общие затраты:

Данный анализ показывает, что затраты пропорциональны 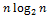 , что меньше, чем у большинства других методов сортировки.
, что меньше, чем у большинства других методов сортировки.
Дерево, как стек или очередь, является одной из широко используемых структур данных во всех языках программирования. С ее помощью организуется файловая структура в любой операционной системе. Она применяется для хранения и представления больших объемов информации в иерархическом виде, а пирамидальная сортировка, основанная на деревьях, является одним из самых быстродействующих и устойчивых алгоритмов сортировки данных.