Построение стереографической проекции кристалла

Графическое изображение кристалла на плоскости производится построением стереографической проекции. Кристалл помещают внутрь сферы, к его всем граням проводят нормали до пересечения со сферой. Для нанесения проекций граней верхней половины кристалла выбирается точка зрения на южном полюсе сферы. Точки пересечения нормалей верхней половины сферы соединяются с южным полюсом, а точки пересечения линий соединения концов нормалей с экваториальной плоскостью - проекции граней верхней половины кристаллов. Следует отметить, что горизонтальные грани, перпендикулярные оси Z, будут иметь нормали, пересекающие сферу на северном полюсе, и проекции в центре круга проекции. Вертикальные грани будут иметь нормали, лежащие в плоскости экватора, и их проекции будут лежать на круге проекций. Наклонные грани будут иметь проекции между центром и кругом проекции.

Для нанесения проекции граней нижней половины кристалла, точка зрения переносится с южного полюса на северный. Концы нормалей, пересекающие сферу, соединяются с полюсом, и точки пересечения линий с плоскостью проекции будут проекцией граней нижней половины кристалла. В отличие от проекций граней верхней половины кристалла, которые отмечаются кружочками, проекции нижней половины граней кристалла отмечаются на проекции крестиками. Это принцип построения стереографической проекции.

Согласно закону постоянства двугранных углов характерными константами кристаллов являются их угловые величины. Поэтому из множества методов проектирования в кристаллографии преимущественно применяются те, которые дают точное понятие об углах на кристаллах. В этом отношении особенно удобны стереографические проекции. «Стереос» (греч.) - пространственный. Примем некоторую точку О за центр проекций (рис.4.)

 

 

Рис.4. Построение стереографической проекции а направления ОА.

 

Произвольным радиусом опишем вокруг О шар, называющейся шаром проекций. Через ту же точку О проведём горизонтальную плоскость Q, являющуюся плоскостью проекций. В результате пересечения сферической поверхности с Q имеем большой круг (линии пересечения поверхности шара с плоскостями, проходящими через его центр), отвечающий экватору шара проекций и представляющий круг проекций. Вертикальный диаметр шара NS, перпендикулярный к Q, называется осью проекций. Такая ось пересекает шар проекций в двух точках – N и S. Одна из этих точек (южный полюс шара проекций – S) является точкой зрения.

Если требуется изобразить стереографическую проекцию какого-либо направления или плоскости, переносим их параллельно самим себе так, чтобы они прошли через центр О.

Рассмотрим получение стереографической проекции некоторого направления ОА (рис.4). Для этого продолжим данное направление до пересечения с поверхностью шара проекций. Пусть точка а₁ представляет собой результат пересечения ОА с шаровой поверхностью. Соединим точку а₁ с точкой зрения S лучом зрения S а₁. Точка а - точка пересечения S а₁ с плоскостью Q – является стереографической проекцией направления ОА. Таким образом, стереографические проекции направлений изображаются точками. Найдём стереографическую проекцию плоскости R. Предварительно перенесём R параллельно самой себе в центр проекций, продолжим её до пересечения с поверхностью шара проекций (рис.5).

 

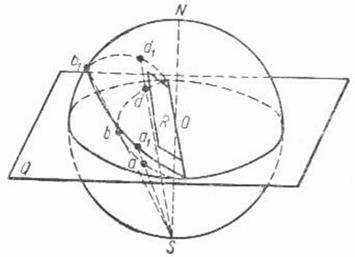
Рис.5. Построение стереографической проекции а в d плоскости R.

В результате пересечения получим на шаре дугу большого круга а₁в₁d₁… Все точки этой окружности соединяем лучами зренияSа₁Sв₁Sd₁c точкой зрения S. Указанные лучи образуют проектирующий конус с вершиной S. Результат пересечения проектирующего конуса с плоскостью проекций Q соответствует стереографической проекции заданной плоскости.

Известна теорема, согласно которой стереографическая проекция круга является также кругом. Таким образом, дуга большого круга а₁в₁d₁… даёт на стереографической проекции дугу окружности авd. В общем случае, стереографические проекции плоскостей изображаются круговыми дугами. Перейдём к проектированию кристаллов методом стереографических проекций.

Пусть задан некоторый кристаллический многогранник. Примем какую-либо точку О внутри него, например центр тяжести, за центр проекций (рис.6.). Из этой точки произвольным радиусом опишем сферическую поверхность – шар проекций. Через центр проведём горизонтальную плоскость проекций Q и условимся весь чертёж изображать на ней. Опустим из центра О на все грани кристалла перпендикуляры и продолжим их до пересечения с поверхностью сферы. В результате пересечений на сферической поверхности возникнет ряд точек. Например, на рис. 6, а нормаль к грани А даёт на шаровой поверхности точку а₁

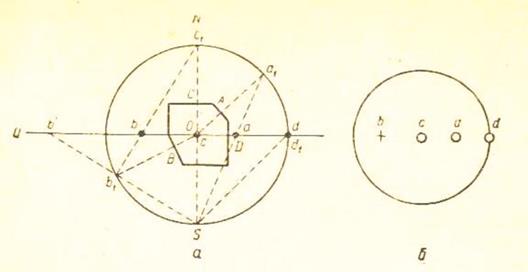
Рис.6. Проектирование кристалла методом стереографических проекций (а); изображение проекций граней А, В, С и D на плоскости Q (б)

 

Все найденные точки следует перенести на горизонтальную плоскость проекций Q . С этой целью южный полюс шара S принимаем за точку зрения и соединяем с ней лучами зрения точки, расположенные на сфере. В результате пересечения лучей зрения с плоскостью чертежа получим новые точки, отвечающие стереографическим проекциям нормалей к граням. Таким образом, грани на данной проекции изображаются точками (точка а – стереографическая проекция нормали к грани А (рис.6). Нормали к граням, пересекающие шар проекций в верхней полусфере , проектируются внутри круга проекций (например, нормаль ОА на рис. 6).Наоборот, нормали, пересекающие шар проекций в нижней полусфере, проектируются вне этого круга (например, нормаль ОВ на рис.6). Неудобство последнего построения заставляет переносить для таких нормалей точку зрения S в северный полюс сферы N. В этом случае и проекции нижних граней окажутся внутри круга проекций. Чтобы отличить друг от друга проекции нормалей к верхним и нижним граням, первые обозначаются кружками, а вторые – крестиками. Необходимо запомнить:

1. горизонтальные грани проектируются в центре круга проекций (например, грань С, на рис.6);

2. вертикальные грани проектируются на самом круге проекций (например, грань D на рис.6);

3. косые грани проектируются внутри круга проекций (например, грани А и В). Чем круче наклон грани (т.е.чем меньше угол между гранью и осью проекций), тем ближе проектирующая её точка располагается к кругу проекций. И, чем положе грань(чем больше указанный угол), тем ближе соответственная точка к центру круга.