ПРОВЕРКА ОСНОВНОГО ЗАКОНА ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА

Цель работы: экспериментальное изучение законов динамики вращательного движения с помощью маятника Обербека.

Приборы и принадлежности: прибор Обербека, штангенциркуль, миллиметровая линейка, электрический секундомер, набор грузов. Установка Elwro.

 

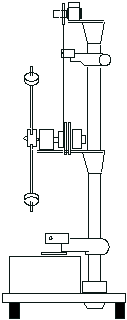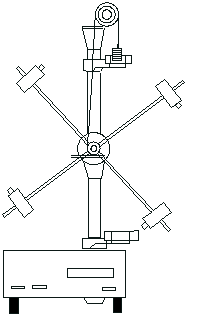Маятник Обербека представляет крестовину, укрепленную на двойном шкиве. Ось вращения крестовины устанавливается горизонтально и закреплена в подшипниках (рис. 15). Вращение прибора осуществляется с помощью нити, намотанной на шкив. Изменение силы натяжения производится с помощью грузов различной массы, прикрепленных к свободному концу нити. Изменение момента инерции прибора достигается передвижением четырех грузов одинаковой массы и формы по направляющим крестовины. Уравнение вращательного движения прибора (при пренебрежении силами трения) связывает три величины: момент силы натяжения нити, угловое ускорение и момент инерции прибора Момент силы натяжения нити и угловое ускорение можно вычислить, зная ускорение а поступательного движения подвешенного груза.

 

Рис. 15

 

Ускорение определяется по значениям расстояния, пройденного грузом и соответствующего промежутка времени. Таким образом, можно рассчитать момент инерции прибора с помощью величин, измеренных в эксперименте. Для падающего груза

 

 

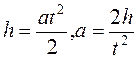
Основное уравнение динамики вращательного движения для вращающейся части маятника.

 

 

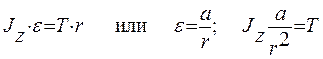
Второй закон Ньютона для поступательно движущегося груза массой М в проекции на направление движения.

 

М × а = М × g – T

 

Отсюда

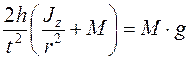
а для момента инерции J_z получается следующее выражение:

 

 

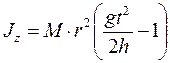
где М - масса груза, подвешенного к нити;

r— радиус шкива;

h— расстояние, пройденное грузом;

t— время, за которое груз прошел расстояние h;

g— ускорение свободного падения.