Проинтегрировать тригонометрическое выражение.
Найти неопределенный интеграл от выражения, содержащего квадратный трехчлен.
Вариант 1.
1) 
2) 
Вариант 2.
1) 
2) 
Вариант 3.
1) 
2) 
Вариант 4.
1) 
2) 
Вариант 5.
1) 
2) 
Вариант 6.
1) 
2) 
Вариант 7.
1) 
2) 
Вариант 8.
1) 
2) 
Вариант 9.
1) 
2) 
Вариант 10.
1) 
2) 
Вариант 11.
1) 
2) 
Вариант 12.
1) 
2) 
Вариант 13.
1) 
2) 
Вариант 14.
1) 
2) 
Вариант 15.
1) 
2) 
Вариант 16.
1) 
2) 
6.5. Проинтегрировать дробно-рациональную функцию.
Вариант 1.
1) 
2) 
3) 
Вариант 2.
1) 
2) 
3) 
Вариант 3.
1) 
2) 
3) 
Вариант 4.
1) 
2) 
3) 
Вариант 5.
1) 
2) 
3) 
Вариант 6.
1) 
2) 
3) 
Вариант 7.
1) 
2) 
3) 
Вариант 8.
1) 
2) 
3) 
Вариант 9.
1) 
2) 
3) 
Вариант 10.
1) 
2) 
3) 
Вариант 11.
1) 
2) 
3) 
Вариант 12.
1) 
2) 
3) 
Вариант 13.
1) 
2) 
3) 
Вариант 14.
1) 
2) 
3) 
Вариант 15.
1) 
2) 
3) 
Вариант 16.
1) 
2) 
3) 
Проинтегрировать тригонометрическое выражение.
Вариант 1.
1) 
2) 
3) 
Вариант 2.
1) 
2) 
3) 
Вариант 3.
1) 
2) 
3) 
Вариант 4.
1) 
2) 
3) 
Вариант 5.
1) 
2) 
3) 
Вариант 6.
1) 
2) 
3) 
Вариант 7.
1) 
2) 
3) 
Вариант 8.
1) 
2) 
3) 
Вариант 9.
1) 
2) 
3) 
Вариант 10.
1) 
2) 
3) 
Вариант 11.
1) 
2) 
3) 
Вариант 12.
1) 
2) 
3) 
Вариант 13.
1) 
2) 
3) 
Вариант 14.
1) 
2) 
3) 
Вариант 15.
1) 
2) 
3) 
Вариант 16.
1) 
2) 
3) 
Во всех дальнейших заданиях каждому из вариантов соответствует только одна задача. Номер варианта отмечен римской цифрой.
Определенный интеграл
6.7. Вычислить определенный интеграл по формуле
Ньютона-Лейбница.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
6.8. Найти среднее значение функции 
на заданном отрезке.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
6.9. Вычислить несобственный интеграл с бесконечными пределами (если он сходится) или установить его расходимость.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
6.10. Вычислить несобственный интеграл от неограниченной функции на конечном отрезке (если он сходится) или доказать его расходимость.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
6.11. Приложения определенного интеграла.
Вычислить:
а) площадь плоской фигуры, ограниченной заданными кривыми, дать чертеж.
б) длину дуги кривой.
в) объем тела вращения вокруг оси ox плоской фигуры, ограниченной заданными линиями, дать чертеж.
I
а) 
б) 
в) 
II
а) 
б) 
в) 
III
а) 
б) 
в) 
IV
а) 
б) 
в) 
V
а) 
б) 
в) 
VI
а) 
б) 
в) 
VII
а) 
б) 
в) 
VIII
а) 
б) 
в) 
IX
а) 
б) 
в) 
X
а) 
б) 
в) 
XI
а) 
б) 
в) 
XII
а) 
б) 
в) 
XIII
а) 
б) 
в) 
XIV
а) 
б) 
в) 
XV
а) 
б) 
в) 
XVI
а) 
б) 
в) 
Функции нескольких переменных.
6.12. Найти частные производные и полный дифференциал функции двух переменных 
в заданной точке 
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
6.13. Вычислить приближенно заданное выражение.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
Двойной интеграл
6.14. Вычислить двукратный интеграл и представить графически область интегрирования.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
6.15. Переходя к полярным координатам, вычислить заданные двойные интегралы.
I. 
,где 
– полукруг радиуса 
с центром в начале координат 
II. 
,где – круг 
.
III. ,где – круг 
.
IV. 
,где – четверть круга радиуса с центром в начале координат 
V. 
,где – четверть круга радиуса с центром в начале координат 
VI. 
,где – круг 
.
VII. 
,где – круг 
.
VIII. 
,где – четверть круга радиуса 
с центром в начале координат 
IX. 
,где – четверть круга радиуса 
с центром в начале координат 
X. 
,где – полукруг радиуса с центром в начале координат 
XI. 
,где – четверть круга радиуса с центром в начале координат ( 
XII. 
,где – полукруг радиуса 
с центром в начале координат 
XIII. 
,где – полукруг 
.
XIV. 
,где. – полукруг 
XV. 
,где – полукруг радиуса 
с центром в начале координат
XVI. 
,где – четверть круга радиуса с центром в начале координат 
6.16 Дать чертеж и вычислить координаты центра тяжести однородной пластины заданной в форме:
I. треугольника с вершинами в точках 
II.фигуры, ограниченной кривыми 
.
III.четверти эллипса 
.
IV.фигуры, ограниченной кривой 
, осью ox и осью oy.
V.фигуры, определяемой в полярных координатах неравенствами: 
VI.треугольника с вершинами в точках 
VII.фигуры, ограниченной кривыми 
.
VIII.четверти эллипса 
.
IX.фигуры, ограниченной кривой 
, осью ox и осью oy.
X.фигуры, определяемой в полярных координатах неравенствами: 
XI.треугольника с вершинами в точках 
XII.фигуры, ограниченной кривыми 
.
XIII.четверти круга 
.
XIV.фигуры, ограниченной кривыми 
XV.фигуры, определяемой в полярных координатах неравенствами: 
XVI.треугольника с вершинами в точках 
6.17. Вычислить моменты инерции однородной пластины заданной формы относительно указанных осей.
I. Треугольника, ограниченного прямыми 
относительно оси 
II. Прямоугольника со сторонами 1 и 2 относительно оси, проходящей через меньшую сторону.
III.Треугольника, ограниченного прямыми 
относительно оси 
IV.Пластины в форме треугольника с вершинами 
относительно оси ox.
V.Квадрата, ограниченного линиями 
относительно начала координат.
VI.Плоской фигуры, ограниченной линиями 
относительно оси ox.
VII.Кольцевой пластины 
относительно оси ox.
VIII.Четверти кольца 
относительно начала координат.
IX.Треугольника, ограниченного прямыми 
относительно оси 
X.Прямоугольника со сторонами 2 и 3 относительно оси, проходящей через большую сторону
XI.Треугольника, ограниченного прямыми 
относительно оси 
.
XII.Пластины в форме треугольника с вершинами 
относительно оси .
XIII.Плоской фигуры, ограниченной линиями 
относительно оси .
XIV.Плоской фигуры, ограниченной линиями 
относительно оси .
XV.Кольцевой пластины 
относительно начала координат.
XVI.Полукольца 
относительно оси .
Криволинейный интеграл
6.18. Вычислить криволинейный интеграл.
Варианты I – V: вычислить интеграл вдоль указанной кривой от точки
до точки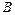 
.
Варианты VI – X: вычислить интеграл вдоль кривой 
, заданной
параметрически.
Варианты XI – XVI: вычислить интеграл по замкнутому контуру ,
проходя его в положительном направлении; использовать
формулу Грина. В вариантах XIV – XVI формулу Грина
проверить непосредственными вычислениями интегралов.
I. 
; 
; 
II. 
; 
; 
III. 
; 
; 
IV. 
; 
; 
V. 
; 
; 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
; – окружность 
.
XII. 
; – окружность 
.
XIII. 
; – окружность 
.
XIV. 
; – треугольник с вершинами 
.
XV. 
; – треугольник с вершинами 
.
XVI. 
; – треугольник с вершинами 
.
6.19. Вычислить криволинейный интеграл от выражения, являющегося полным дифференциалом.
I. 
II. 
III. 
IV. 
V. 
VI. 
VII. 
VIII. 
IX. 
X. 
XI. 
XII. 
XIII. 
XIV. 
XV. 
XVI. 
ЛИТЕРАТУРА
1. Бодунов М.А., Бородина С.И., Теуш Б.Л., Ткаченко О.И. Интегральное исчисление функций одной и нескольких переменных. Теория поля. – М., МАМИ, 2003.
2. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. Т. 1, 2 – М., Высшая школа, 1978.
3. Пискунов Н.С. Дифференциальное и интегральное исчисления.
Т. 1, 2. – М., Наука, 1985.
4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М., Наука, 1988.
5. Задачи и упражнения по математическому анализу для втузов. Под редакцией Демидовича Б.П. – М., АСТ, 2001.
6. Данко И.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Т. 1, 2. – М., Высшая школа, 1996.
7. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука. Физматлит., 1986.