Концепция криптосистемы с открытым ключом

Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования – другой ключ (отсюда и название – асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.

Для расшифрования данных получатель зашифрованной информации использует второйключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.

Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рис. 4.1. В этой криптосистеме применяют два различных ключа: Кв – открытый ключ отправителя А; kв – секретный ключ получателя В. Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ kв по незащищенному каналу). Значения ключей Кв и kв зависят от начального состояния генератора ключей.

Раскрытие секретного ключа kв по известному открытому ключу Кв должно быть вычислительно неразрешимой задачей.

Характерные особенности асимметричных криптосистем:

1. Открытый ключ Кв и криптограмма С могут быть отправлены по незащищенным каналам, т.е. противнику известны Кв и С.

2. Алгоритмы шифрования и расшифрования

Ев : М ® С,

Dв : С ® М

являются открытыми.

Рисунок 4.1 – Обобщенная схема асимметричной криптосистемы с открытым ключом

Защита информации в асимметричной криптосистеме основана на секретности ключа kв.

У.диффи и м.хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:

1. Вычисление пары ключей (Кв, kв) получателем В на основе начального условия должно быть простым.

2. Отправитель А, зная открытый ключ Кв и сообщение М, может легко вычислить криптограмму

С = 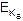(М) = Ев (М). (4.1)

3. Получатель В, используя секретный ключ kв и криптограмму С, может легко восстановить исходное сообщение

М = (С) = Dв(С) = Dв [Ев(М)]. (4.2)

4. Противник, зная открытый ключ Кв, при попытке вычислить секретный ключ kв наталкивается на непреодолимую вычислительную проблему.

5. Противник, зная пару (Кв, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему [28].