Равновесная концентрация. Связь концентраций электронов и дырок в собственном и примесном полупроводниках. Эффект подавления.
Объем одного квантового состояния в фазовом пространстве. Функция плотности энергетических состояний.
Чтобы вычислять плотность состояний энергии для частицы, мы сначала вычислим плотность состояний в обратном пространстве (импульсное или k-пространство). Расстояние между состояниями задано граничными условиями. Для свободных электронов и фотонов в пределах ящика размера L, и для электронов в кристаллической решётке с размером решётки L используем периодические граничные условия Борна — фон Кармана. Используя волновую функцию свободной частицы получаем
\begin{matrix}
e^{ikx} & = & e^{ik(x + L)} \\
1 & = & e^{ikL} \\
2\pi n & = & kL \\
\frac{2\pi}{L_x} & = & \Delta k \\
\end{matrix}
где n — любое целое число, а \Delta k\, — расстояние между состояниями с различными k.
Полное количество k-состояний, доступных для частицы - объем k-пространства доступного для неё, разделённого на объём k-пространства, занимаемого одним состоянием. Доступный объем - просто интеграл от k = 0 к k = k. Объём k-пространства для одного состояния в n-мерном случае запишется в виде
G(k) = \frac{g_s}{\left( {\Delta k,} \right)^n} \int\limits_0^k\,{d^n{\mathbf{k}}},
g_s — вырождение уровня (обычно это спиновое вырождение, равное 2). Это выражение нужно продифференцировать, чтобы найти плотность состояний в k-пространстве: g(k)\,dk = \frac{dG(k)}{dk}\,dk. Чтобы найти плотность состояний по энергии, нужно знать закон дисперсии для частицы, то есть выразить k и dk в выражении g(k)dk в терминах E и dE. Например для свободного электрона: E = \frac{p^2}{2m} = \frac{(\hbar k)^2}{2m}, dE = \frac{\hbar^2 k}{m}\,dk.
С более общим определением связано соотношение
D(E) = \sum_s~\delta(E-E_s)\,
где индекс s соответствует некоторому состоянию дискретного или непрерывного спектра, а \delta — дельта-функция Дирака. При переходе от суммирования к интегрированию следует использовать правило
\sum_s\rightarrow \int\frac{d^np~d^nq}{(2\pi\hbar)^n}\,
где \hbar — постоянная Планка.
Идеальный Ферми-газ. Связь энергии Ферми и концентрации электронов.
Идеальный Ферми-газ. Средняя энергия электрона.
Виды связей атомов и молекул в кристаллах. Аморфное и кристаллическое состояния. Кристаллическая решетка. Период решетки. Состояния электронов в кристалле. Понятие квазиимпульса.
Модель Кронига-Пени. Волновая функция электрона.
Модель Кронига-Пени. Энергетические зоны. Зоны Бриллюэна. Связь энергетических зон и уровней энергии электрона в потенциальной яме с бесконечно высокими стенками.
Классификация кристаллов по структуре энергетических зон. Зона проводимости и валентная зона. Эффективная масса электрона и дырки.
Определение собственного полупроводника. Возникновение электропроводности собственного полупроводника с точки зрения модельных представлений и зонной теории. Расчет концентрации электронов в зоне проводимости произвольного полупроводника.
Собственный полупроводник-это чистый полупроводник, содержание посторонних примесей в котором не превышает 10−8 … 10−9%. Концентрация дырок в нём всегда равна концентрации свободных электронов, так как она определяется не легированием, а собственными свойствами материала, а именно термически возбуждёнными носителями, излучением и собственными дефектами.
Полупроводник без примесей обладает собственной электропроводностью, которая имеет два вклада: электронный и дырочный. Если к полупроводнику не приложено напряжение, то электроны и дырки совершают тепловое движение и суммарный ток равен нулю. При приложении напряжения в полупроводнике возникает электрическое поле, которое приводит к возникновению тока, называемого дрейфовым током iдр. Полный дрейфовый ток является суммой двух вкладов из электронного и дырочного токов:
iдр= in+ ip,
где индекс n соответствует электронному вкладу, а p - дырочному.
В полупроводниках при повышении температуры вследствие генерации электрон-дырочных пар концентрация электронов в зоне проводимости и дырок в валентной зоне увеличивается значительно быстрее, нежели уменьшается их подвижность, поэтому с повышением температуры проводимость растет. Процесс гибели электрон-дырочных пар называется рекомбинацией. Фактически проводимость собственного полупроводника сопровождается процессами рекомбинации и генерации и если скорости их равны, то говорят что полупроводник находится в равновесном состоянии.
Количество разрешённых состояний для электронов в зоне проводимости (определяемая плотностью состояний) и вероятность их заполнения (определяемая функцией Ферми — Дирака) и соответственные величины для дырок задают количество собственных электронов и дырок в полупроводнике:
n=Nc*exp((Ec-Ef)/kT)
p=Nv*exp((Ev-Ef)/kT)
где Nc, Nv — константы определяемые свойствами полупроводника, Ec и Ev — положение дна зоны проводимости и потолка валентной зоны соответственно,Ef- неизвестный уровень Ферми, k — постоянная Больцмана, T — температура.
23. Определение собственного полупроводника. Возникновение электропроводности собственного полупроводника. Условие электронейтральности. Расчет уровня Ферми и удельной электропроводности собственного полупроводника. Графики n = f(T), f(Т), Lnf(1/T).. Экспериментальное определение ширины ЗЗ.
Собственный полупроводник или полупроводник i-типа или нелегированный полупроводник (англ. intrinsic — собственный) — это чистый полупроводник, содержание посторонних примесей в котором не превышает 10−8 … 10−9%. Концентрация дырок в нём всегда равна концентрации свободных электронов, так как она определяется не легированием, а собственными свойствами материала, а именно термически возбуждёнными носителями, излучением и собственными дефектами. Концентрация подвижных носителей заряда зависит от температуры кристалла и ширины запрещенной зоны: концентрация носителей заряда возрастает с повышением температуры и уменьшением ширины запрещенной зоны. Следовательно, удельная электрическая проводимость полупроводника, пропорциональная концентрации носителей заряда, также увеличивается с повышением температуры, а ее значение больше в полупроводниках с меньшим значением ширины запрещающей зоны (?Wз). Свободный электрон, совершая хаотическое движение, может заполнить дырку в ковалентной связи. Тогда разорванная ковалентная связь восстанавливается, а пара носителей заряда (электрон и дырка) исчезает, т.е. происходит рекомбинация носителей заряда противоположных знаков. Этот процесс сопровождается выделением избыточной энергии в виде тепла или света. На энергетической диаграмме (рис. 1.5) рекомбинация соответствует переходу электрона из зоны проводимости на вакантный уровень в валентной зоне.
Оба процесса – генерация пар носителей заряда и их рекомбинация – в любом объеме полупроводника происходят одновременно. Соответствующая концентрация носителей заряда устанавливается из условия динамического равновесия, при котором число вновь возникающих носителей заряда равно числу рекомбинирующих. Промежуток времени между моментом генерации носителя заряда и его рекомбинацией называют временем жизни свободного электрона или дырки, а пройденное носителем заряда за время жизни расстояние – длиной свободного пробега. Учитывая, что время жизни отдельных носителей заряда различно, под этими терминами понимают среднее время жизни и среднюю длину свободного пробега.
ровень Ферми - основной параметр статистического распределения электронов и дырок. В расчетах для определения положения уровня Ферми, как правило, используют условие электронейтральности.
Для собственного полупроводника n=p.
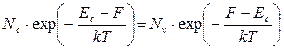
| (2.13) |
После логарифмирования (2.13) сравнительно просто рассчитывается значение уровня Ферми:
| (2.14) |
Из выражения (2.14) следует, что при температуре абсолютного нуля уровень Ферми для собственного полупроводника располагается посередине запрещенной зоны :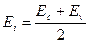 
.
Для собственного полупроводника вводится понятие собственной концентрации с помощью условия ni2 = np. Откуда:
 
| (2.15) |
| (2.16) |
При расчете собственной концентрации необходимо учитывать зависимость ширины запрещенной зоны от температуры (1.17). Собственная концентрация является важным характеристическим параметром материала, поскольку для заданной температуры ni2 –величина постоянная не только для собственных, но и для легированных материалов (она не зависит от положения уровня Ферми). Значения собственной концентрации для основных полупроводниковых материалов представлены в таблице.
24. Определение донорного полупроводника и донорной примеси. Электропроводность донорного полупроводника при высокой и низкой температурах. Температура примесного истощения. Условие электронейтральности. Графики n = f(T), f(Т), Lnf(1/T). в широком интервале температур.
Донорный проводник и донорная примесь. Электропроводность донорного проводника при высокой и низкой температуре . Условия электронейтральности.
ферми
25. Расчет уровня Ферми донорного полупроводника. Расчет удельной электропроводности донорного полупроводника. Графики n = f(T), f(T), Ln f(1/T) в широком интервале температур.
Равновесная концентрация. Связь концентраций электронов и дырок в собственном и примесном полупроводниках. Эффект подавления.
Рассмотрим общий случай, когда концентрация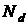 
мелких доноров отличается от концентрации 
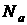мелких акцепторов. Для определенности положим, что 
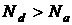. В этом случае мелкие доноры и мелкие акцепторы в количестве 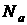будут взаимно компенсированы, т.е. все акцепторы будут заполнены электронами пришедшими с донорных центров, следовательно, 
. Число некомпенсированных доноров способных участвовать в тепловой генерации электронов в с – зону будет равно: 
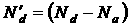- эффективная концентрация доноров. Значит, при соотношении 
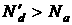полупроводник ведет себя как полупроводник 
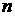- типа. В таком полупроводнике нет примесных дырок, а есть дырки образуемые в результате собственных переходов при высоких температурах. Уравнение электронейтральности для такого полупроводника с учетом предыдущего параграфа будет иметь вид:
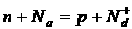(1)
Рассмотрим несколько придельных случаев.
1. Очень низкие температуры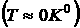 
.
В этом случае 
, 
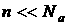. Тогда уравнение электронейтральности примет вид:
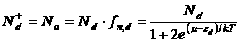(2)
(3)
1. 
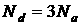
2. 
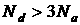
3. 
Подставим (3) в выражение для 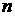, получим:
(4)
Видно, что энергия активации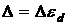 
.
2. Низкие температуры.
В этом случае 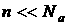, . Тогда уравнение электронейтральности примет вид:
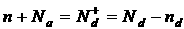(5)
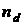- концентрация доноров занятых электронами.
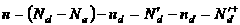(6)
- эффективная концентрация ионизированных доноров.
Такое уравнение решено в §4.
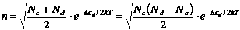(7)
Видно, что энергия активации 
.
3. Высокие температуры.
В этом случае нельзя пренебрегать величиной 
, 
. Тогда уравнение электронейтральности примет вид:
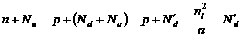(8)
Решение этого уравнения в §5. При высоких температурах:
(9)
По величине 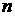, в этой области можно определить эффективную концентрацию 
.
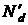4. Очень высокие температуры.
(10)
27. Скорость генерации. Тепловая генерация. Скорость рекомбинации. Коэффициент рекомбинации. Равновесное и стационарное состояния. Избыточная концентрация. Закон убыли избыточной концентрации со временем. Время жизни неосновных носителей. Графики Dр(t), р(t) (или Dn(t), n(t).
Под действием приложенного к кристаллу напряжения в нем возникает электрическое поле. Движение носителей заряда упорядочивается: электроны перемещаются по направлению к положительному электроду, дырки – к отрицательному. При этом не прекращается и тепловое движение носителей заряда, вследствие которого происходят столкновения их с атомами полупроводника и примеси.
Направленное движение носителей заряда под действием сил электрического поля называют дрейфом, а вызванный этим движением ток – дрейфовым током. При этом характер тока может быть электронным, если он вызван движением электронов, или дырочным, если он создается направленным перемещением дырок.
Средняя скорость носителей заряда в электрическом поле прямо пропорциональна напряженности электрического поля:
Коэффициент пропорциональности m называют подвижностью электронов (mn), или дырок (mp). Свободные электроны движутся в пространстве между узлами кристаллической решетки, а дырки – по ковалентным связям, поэтому средняя скорость, а следовательно, и подвижность электронов больше, чем дырок. У кремния подвижность носителей заряда меньше, чем у германия.
В собственных полупроводниках концентрации электронов и дырок одинаковы, но вследствие их разной подвижности электронная составляющая тока больше дырочной. В примесных полупроводниках концентрации электронов и дырок существенно отличаются, характер тока определяется основными носителями заряда: в полупроводниках р-типа – дырками, а в полупроводниках n-типа – электронами.
При неравномерной концентрации носителей заряда вероятность их столкновения друг с другом больше в тех слоях полупроводника, где их концентрация выше. Совершая хаотическое тепловое движение, носители заряда отклоняются в сторону, где меньше число столкновений, т.е. движутся в направлении уменьшения их концентрации.
Направленное движение носителей заряда из слоя с более высокой их концентрацией в слой, где концентрация ниже, называют диффузией, а ток, вызванный этим явлением, – диффузионным током. Этот ток, как и дрейфовый, может быть электронным или дырочным.
Степень неравномерности распределения носителей заряда характеризуется градиентом концентрации; его определяют как отношение изменения концентрации к изменению расстояния, на котором оно происходит. Чем больше градиент концентрации, т.е. чем резче она изменяется, тем больше диффузионный ток.
Электроны, перемещаясь из слоя с высокой концентрацией в слой с более низкой концентрацией, по мере продвижения рекомбинируют с дырками, и наоборот, диффундирующие в слой с пониженной концентрацией дырки рекомбинируют с электронами. При этом избыточная концентрация носителей заряда уменьшается.