ЗАКОН РАСПРЕДЕЛЕНИЯ ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

 

Случайной величиной называется величина, которая в результате опыта может принимать любое из своих возможных значений, причем заранее неизвестно какое именно.

Если множество возможных значений случайной величины конечно или счетно (т.е. все элементы множества могут быть пронумерованы натуральными числами), то случайная величина называется дискретной.

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.Закон распределения дискретной случайной величины может быть задан в виде таблицы, первая строка которой содержит возможные значения х_i, а вторая – вероятности р_i:

 

			…
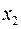
pi			…

где

Задачи

8.1.В урне 4 белых и 3 черных шара. Из нее последовательно вынимают шары до первого появления белого шара. Построить ряд и многоугольник распределения д. с. в. – числа извлеченных шаров.

8.2.В урне 4 белых и 3 черных шара. Из нее наудачу извлекли три шара. Найти:

а) ряд распределения д.с.в. – числа извлеченных белых шаров;

б) вероятность события А = {извлечено не менее 2-х белых шаров}.

8.3.Три стрелка, ведущие огонь по цели, сделали по одному выстрелу. Вероятности их попадания в цель соответственно равны 0,5, 0,6, 0,8. Построить ряд распределения с. в. – числа попаданий в цель.

8.4.Вероятность того, что автомат при опускании одной монеты срабатывает правильно, равна 0,98. Построить ряд распределения с. в. – числа опусканий монет в автомат до первого правильного срабатывания автомата. Найти вероятность того, что будет опущено 5 монет. Решить ту же задачу при условии, что в наличии всего 3 монеты.

8.5.Построить ряд распределения числа попаданий в ворота при двух одиннадцатиметровых ударах, если вероятность попадания при одном ударе равна 0,7.

8.6.Дискретная с.в. задана рядом распределения:

	-2
pi	0,08	0,40	0,32	0,2

Найти:

а) функцию распределения ;

б) вероятности событий А={ }; В= ;С= ;

в) построить график функции F(x).

8.7.Найти функцию распределения случайной величины , закон которой был получен при решении задачи 8.1.

8.8.В команде 16 спортсменов, из которых 6 перворазрядников. Наудачу выбирают 2 спортсменов. Построить ряд распределения и функцию распределения числа перворазрядников среди выбранных.

8.9.Даны законы распределения двух независимых случайных величин и :

	0,3	0,5	0,2

 

	-2	-1
	0,4	0,6

Найти закон распределения величин: а) ; б)

8.10.Подброшены две игральные кости. Построить ряд распределения:

а) суммы выпавших очков; б) разности выпавших очков.

8.11.Вероятность того, что студент найдет в библиотеке нужную ему книгу, равна 0,4. Построить ряд распределения числа библиотек, которые он может посетить, если ему доступны четыре библиотеки.

8.12.АТС обслуживает 1500 абонентов. Вероятность того, что в течение трех минут на АТС поступит вызов от одного абонента, равна 0,002. Построить ряд распределения с. в. – числа вызовов, поступивших на АТС в течение трех минут. Найти вероятность того, что за это время поступит более трех вызовов.

8.13.В партии, содержащей 20 изделий, имеется четыре изделия с дефектами. Наудачу отобрали три изделия для проверки ихкачества. Построить ряд распределения числа дефектных изделий, содержащихся в указанной выборке.

8.14.Записать законы распределения следующих случайных величин:

а) числа промахов при четырех выстрелах, если вероятность промаха при одном выстреле равна q;

б) числа выстрелов до первого попадания при четырех патронах, если вероятность попадания при одном выстреле равна p;

в) при неограниченном числе патронов.

8.15.Две игральные кости бросают дважды. С.в. – число выпадений четного числа очков на обеих костях. Составить закон распределения этой случайной величины.

8.16.Два баскетболиста бросают мяч в корзину до тех пор, пока один из них не попадет. Вероятность попадания при одном броске для первого баскетболиста 0,4, а для второго – 0,6. Составить законы распределения числа бросков для каждого баскетболиста, если известно, что броски начинает первый баскетболист.

8.17.Задана функция распределения д.с.в. :

Вычислить: ,