ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА

 

Если событие может произойти одновременно с одним из событий , представляющих собой так называемую полную группу попарно несовместных событий(то есть в результате опыта обязательно произойдет одно и только одно событие из этой группы), то события называются гипотезами, а вероятность события определяется по формуле полной вероятности

,

где – вероятность -ой гипотезы, а – условная вероятность события при осуществлении данной гипотезы.

Если известно, что в результате опыта событие произошло, то эта информация может изменить вероятности гипотез: повышаются вероятности тех гипотез, при которых событие происходит с большей вероятностью, и уменьшаются вероятности остальных. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса

.

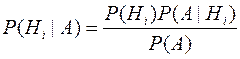В правой части равенства в знаменателе дроби стоит полная вероятность события .

 

Задачи

6.1.В ящике имеется 8 пистолетов одной системы и одинаковые по виду. Из них два непристрелянных. Вероятность попасть в цель из непристрелянного пистолета 0,4, а из пристрелянного 0,8. Какова вероятность того, что выстрел из случайно взятого пистолета даст попадание?

6.2.45 % телевизоров, имеющихся в магазине, изготовлены на 1-м заводе, 15 % – на 2-м, остальные – на 3-м заводе. Вероятности того, что телевизоры, изготовленные на этих заводах, не потребуют ремонта в течение гарантийного срока, равны 0,96; 0,84; 0,90 соответственно. Найти вероятность того, что купленный наудачу телевизор выдержит гарантийный срок работы.

6.3.Имеются две одинаковые урны с шарами. В 1-й находится 3 белых и 4 черных шара, во 2-й – 2 белых и 3 черных. Из наудачу выбранной урны вынимают один шар. Какова вероятность того, что этот шар белый?

6.4.Три стрелка произвели по одному выстрелу по намеченной цели. Вероятность попадания 1-м стрелком равна 0,6, 2-м – 0,7, 3-м – 0,8. При одном попадании в мишень вероятность поражения цели равна 0,2, при двух – равна 0,6, при трех – цель заведомо поражается. Найти вероятность поражения цели.

6.5.Техническое устройство выйдет из строя, если откажут не менее двух из трех независимо работающих элементов. Bepoятности отказов 1-го, 2-го, 3-го элементов соответственно равны 0,2; 0,4; 0,3. Известно, что устройство отказало. Найти вероятность того, что отказали 1-й и 2-й элементы.

6.6.Предположим, что 5 % мужчин и 0,25 % всех женщин дальтоники. Наугад выбранное лицо оказалось дальтоником. Считая, что мужчин и женщин одинаковое количество, найти вероятность того, что этот человек:

а) мужчина; б) женщина.

6.7.Система обнаружения самолета из-за наличия помех в зоне действия локатора может давать ложные показания с вероятностью 0,05, а при наличии цели в зоне система обнаруживает ее с вероятностью 0,9. Вероятность появления противника в зоне равна 0,25. Определить вероятность ложной тревоги.

6.8.В магазин поступают одинаковые изделия с трех заводов, причем 1-й завод поставил 50 изделий, 2-й – 30, 3-й – 20 изделий. Среди изделий 1-го завода 70 % первосортных, а среди изделий 2-го – 80 %, 3-го – 90 % первосортных. Куплено одно изделие. Оно оказалось первосортным. Какова вероятность того, что изделие выпущено 1-м заводом?

6.9.В студенческой группе 70 % – юноши. 20 % юношей и 40 % девушек имеют сотовый телефон. После занятий в аудитории был найден кем-то забытый телефон. Какова вероятность того, что он принадлежал:

а) юноше; б) девушке?

6.10.Два стрелка независимо друг от друга сделали по одному выстрелу в мишень. Вероятности их попадания в мишень соответственно равны 0,75 (1-й стрелок) и 0,80 (2-й стрелок). После стрельбы в мишени обнаружена одна пробоина. Какова вероятность того, что в мишень попал 2-й стрелок?

6.11.Военный корабль может пройти вдоль пролива шириной 1 км с минным заграждением в любом месте. Вероятность его подрыва на мине в правой части заграждения шириной 200 м равна 0,3, а на остальной части – 0,8. Найти вероятность того, что корабль благополучно пройдет пролив.

6.12.В 1-й урне находится 7 белых и 5 черных шаров, а во 2-й – 4 белых и 8 черных. Из первой урны наудачу перекладывают во вторую 2 шара, а затем из 2-й урны извлекают один шар. Какова вероятность того, что он окажется белым?

6.13.В вычислительном центре имеются 6 ЭВМ одной фирмы и 4 ЭВМ другой фирмы. Надёжность ЭВМ 1-ой фирмы равна 0,95, а у другой – 0,7. Студент производит расчёт на наудачу выбранной ЭВМ. Найти вероятность того, что до окончания расчёта ЭВМ не выйдет из строя.

6.14.В коробке находится 4 новых и 2 уже использованных теннисных мяча. Для первой игры берут из коробки 2 мяча, а затем их возвращают после игры в коробку. Найти вероятность того, что для второй игры будут вытянуты два новых мяча.

6.15.В магазин поставляются телевизоры тремя фирмами в соотношении 5:2:3. Телевизоры, поступающие от этих фирм, не требуют ремонта в течение гарантийного срока соответственно в 96 %, 92 % и 94 % случаев. Найти вероятность того, что купленный наудачу телевизор не потребует ремонта в течение гарантийного срока.

6.16.На вход радиолокационного устройства с вероятностью 0,7 поступает полезный сигнал с помехами, а с вероятностью 0,3 – только одни помехи. Если поступает полезный сигнал с помехами, то устройство регистрирует наличие сигнала с вероятностью p₁; если только помехи – с вероятностью р₂. Какова вероятность того, что устройство зарегистрирует какой-то сигнал?

6.17.Вероятность отказа прибора при воздействии на него только вибрации равна 0,1, а только перегрева – 0,05; вероятность отказа при воздействии вибрации и перегрева равна 0,2. При эксплуатации прибора вероятность возникновения перегрева равна 0,2, вероятность возникновения вибрации равна 0,3. Перегрев и вибрация возникают независимо. Найти вероятность отказа прибора.

6.18.Из полного набора костей домино наугад берутся две кости. Определить вероятность того, что вторую кость можно приставить к первой.

6.19.Число грузовых автомашин, проезжающих по шоссе с бензоколонкой, относится к числу легковых автомашин, проезжающих по тому же шоссе, как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала машина. Найти вероятность того, что это грузовая машина.