ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Комбинаторика – раздел математики, изучающий различные соединения (комбинации) элементов конечных множеств.
Пусть дано множество, состоящее из n элементов.
Размещениями из n элементов по k элементов ( 
) называется любое упорядоченное подмножество данного множества, содержащее k элементов.
Два размещения различны, если они отличаются друг от друга либо составом элементов, либо порядком их следования.
Число размещений из n элементов по k элементов обозначается символом 
и вычисляется по формуле
.
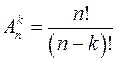Перестановкой из n элементов называется размещение из n элементов по n элементов. Любые перестановки отличаются друг от друга только порядком следования элементов.
Число перстановок из n элементов обозначается символом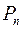 
и вычисляется по формуле
.
Сочетанием из n элементов по k элементов ( ) называется любое подмножество данного множества, содержащее k элементов.
Любые два сочетания отличаются друг от друга только составом элементов.
Число сочетаний из n элементов по k элементов обозначается символом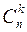 
и вычисляется по формуле
.
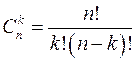Если при выборке k элементовиз n элементы возвращаются обратно, то полученные выборки представляют собой выборки с повторениями.
Число размещений из n элементов по k элементов с повторениями обозначается символом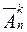 
и вычисляется по формуле
.
Число сочетаний из n элементов по k элементов с повторениями обозначается символом 
и вычисляется по формуле
.
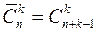Задачи
1.1.Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если:
а) цифры не повторяются; б) цифры могут повторяться; с) числа должны быть нечетными и цифры не повторяются.
Задачу решить двумя способами: используя формулы комбинаторики и используя основные правила комбинаторики.
1.2.На5 сотрудников выделено3 путевки.Сколькими способами их можно распределить, если: а) путевки различны; б) путевки одинаковы.
1.3.Сколько различных «слов» можно составить из всех букв слова ПРИЗМА? Сколько из них таких, в которых буквы Р и И стоят рядом? Сколько таких, в которых эти буквы не стоят рядом? (в комбинаторике под словами понимают любой набор букв, который не обязательно будет словом какого-нибудь языка).
1.4.Четыре студента сдают экзамен. Сколькими способами им могут быть выставлены положительные оценки?
1.5.Имеется 4 разных флага. На флагштоке поднимается сигнал, состоящий не менее чем из двух флагов. Сколько различных сигналов можно подать, если порядок флагов в сигнале учитывается?
1.6.В коробке 10 деталей, из них 7 стандартные. Сколькими способами можно взять из коробки 6 деталей таким образом, чтобы среди них было 4 стандартные детали?
1.7.В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать двух студентов одного пола?
1.8.Из группы в 15 человек выбирают четырех участников эстафеты 800×400×200×100. Сколькими способами можно расставить спортсменов на этих этапах?
1.9.Сколькими способами можно расставить на книжной полке десятитомник произведений Д. Лондона, располагая их:
а) в произвольном порядке;
б) так, чтобы I, V и IX тома стояли рядом (в любом порядке);
в) так, чтобы I, II, IIIтома не стояли рядом (в любом порядке)?
1.10.Вкомнате имеется 7 стульев. Сколькими способами можно разместить на них 7 гостей? 3 гостя?
1.11.Студенты сдают 5 экзаменов, в том числе 2 экзамена по математике. Сколькими способами можно распределить экзамены, но так, чтобы экзамены по математике следовали один за другим? Не следовали один за другим?
1.12.Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькими способами он может выбрать приглашенных?
1.13.Имеется 9 красных и 7 розовых гвоздик. Сколькими способами можно выбрать: а) три любые гвоздики; б) шесть гвоздик одного цвета; с) четыре красных и три розовых гвоздики?
1.14.Группа туристов из 12 юношей и 7 девушек выбирает по жребию 5 человек для приготовления ужина. Сколько существует способов при которых в эту «пятерку» попадут: а) одни девушки; б) 3 юноши и 2 девушки; в) 1 юноша и 4 девушки; г) 5 юношей?
1.15.В магазине 7 видов тортов. Сколькими способами можно приобрести набор из трех тортов? А если имеется три вида тортов, а необходим набор из 7 тортов?
1.16.Пять человек вошли в лифт на первом этаже девятиэтажного дома. Сколькими способами пассажиры могут выйти из лифта на нужных этажах?
1.17.Найти число диагоналей выпуклого десятиугольника.
1.18.Собрание из 40 человек избирает председателя, секретаря и трех членов редакционной коллегии. Сколькими способами это можно сделать?
1.19.В купе железнодорожного вагона один напротив другого два дивана по четыре места. Из 8 пассажиров трое желают ехать по ходу движения поезда, двое – спиной. Сколькими способами можно разместить пассажиров с учетом их пожеланий?
1.20.В некотором государстве не было жителей с одинаковым набором зубов. Какова наибольшая численность этого государства?
1.21.В подъезде дома установлен замок с кодом. Дверь автоматически отпирается, если в определенной последовательности набрать четыре цифры из имеющихся 12. Некто, не зная кода, стал наудачу набирать различные комбинации из 4-х цифр. Какое наибольшее число попыток ему надо предпринять, чтобы дверь открылась?
1.22.12 человек прибыли в гостиницу, в которой есть один 4-местный, два 3-местных и один 2-местный номер. Сколькими способами их можно разместить в этих номерах?