Криволинейное движение

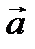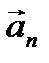При криволинейном движении у вектора скорости изменяется направление. При этом может меняться и его модуль, т. е. длина. В этом случае вектор ускорения раскладывается на две составляющие: касательную к траектории и перпендикулярную к траектории (рис. 10). Составляющая называется тангенциальным (касательным) ускорением, составляющая 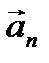–нормальным(центростремительным) ускорением.

Рис. 10.

Ускорение при криволинейном движении

 

Тангенциальное ускорение характеризует быстроту изменения линейной скорости, а нормальное ускорение характеризует быстроту изменения направления движения.

Полное ускорение равно векторной сумме тангенциального и нормального ускорений:

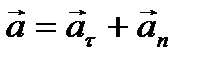(15)

Модуль полного ускорения равен:

.

Рассмотрим равномерное движение точки по окружности. При этом 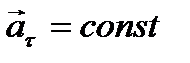и . Пусть в рассматриваемый момент времени t точка находится в положении 1 (рис. 11). Спустя время Δt точка окажется в положении 2, пройдя путь Δs, равный дуге 1—2. При этом скорость точки v получает приращение Δv, в результате чего вектор скорости, оставаясь неизменным по величине, повернется на угол Δφ, совпадающий по величине с центральным углом, опирающимся на дугу длиной Δs:

(16)

где R—радиус окружности, по которой движется точка. Найдем приращение вектора скорости Для этого перенесем вектор так, чтобы его начало совпадало с началом вектора 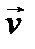. Тогда вектор изобразится отрезком, проведенным из конца вектора 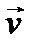в конец вектора . Этот отрезок служит основанием равнобедренного треугольника со сторонам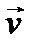и и и углом Δφ при вершине. Если угол Δφ невелик (что выполняется для малых Δt), для сторон этого треугольника можно приближенно написать:

.

Подставляя сюда Δφ из (16), получаем выражение для модуля вектора :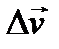

.

Разделив обе части уравнения на Δt и сделав предельный переход, получим величину центростремительного ускорения:

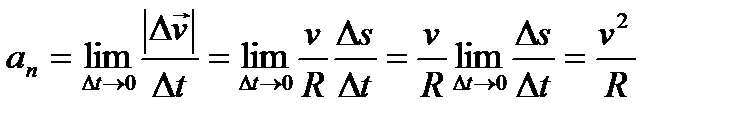. (17)

Здесь величины v и R постоянные, поэтому их можно вынести за знак предела. Предел отношения – это модуль скорости 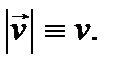Его также называют линейной скоростью.

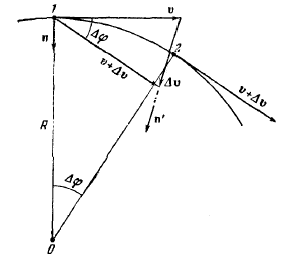
Рис. 11.

Радиус кривизны

 

Радиус окружности R называется радиусом кривизны траектории. Величина, обратная R, называется кривизной траектории:

.

где R — радиус рассматриваемой окружности. Если α есть центральный угол, соответствующий дуге окружности s, то, как известно, между R, α и s имеет место соотношение:

s = Rα. (18)

Понятие радиуса кривизны применимо не только к окружности, но и любой кривой линии. Радиус кривизны (или обратная ему величина – кривизна) характеризует степень изогнутости линии. Чем меньше радиус кривизны (соответственно, чем больше кривизна), тем сильнее изогнута линия. Рассмотрим это понятие подробнее.

Кругом кривизны плоской линии в некоторой точке A называется предельное положение окружности, проходящей через точку А и две другие точки В₁ и В₂ при их бесконечном приближении к точке А (на рис. 12 кривая проведена сплошной линией, а круг кривизны — пунктирной). Радиус круга кривизны дает радиус кривизны рассматриваемой кривой в точке A, а центр этого круга — центр кривизны кривой для той же точки А.

Проведем в точках B₁ и В₂ касательные B₁D и В₂Е к окружности, проходящей через точки В₁, А и B₂. Нормали к этим касательным B₁С и В₂С представят собой радиусы R окружности и пересекутся в ее центре С. Введем угол Δα между нормалями В1С и В₂С; очевидно, он равен углу между касательными В₁D и В₂E. Обозначим участок кривой между точками B₁ и В₂ как Δs. Тогда по формуле (18):

.

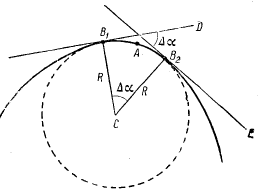
Рис. 12.

Круг кривизны плоской кривой линии

 

Рис. 13.

Определение кривизны плоской кривой в разных точках

 

На рис. 13 изображены круги кривизны плоской линии в разных точках. В точке A₁, где кривая является более пологой, радиус кривизны больше, чем в точке A₂, соответственно, кривизна линии в точке A₁ будет меньше, чем в точке A₂. В точке A₃ кривая является еще более пологой, чем в точках A₁ и A₂, поэтому радиус кривизны в этой точке будет больше, а кривизна меньше. Кроме того, круг кривизны в точке A₃ лежит по другую сторону кривой. Поэтому величине кривизны в этой точке приписывают знак, противоположный знаку кривизны в точках A₁ и A₂: если кривизну в точках A₁ и A₂ будем считать положительной, то кривизна в точке A₃ будет отрицательной.