Решение типовых задач
Задача 1. По данным о месячной заработной плате 10 рабочих трех разных профессий (токарь, слесарь и кузнец) вычислены: общая дисперсия заработной платы  =1636 и средняя из внутригрупповых дисперсий
=1636 и средняя из внутригрупповых дисперсий  =1140. Вычислить корреляционное отношение.
=1140. Вычислить корреляционное отношение.
Решение. Корреляционное отношение вычисляется по формуле
 .
.
Следовательно, сначала необходимо найти межгрупповую дисперсию
 .
.
Подставляя это значение в вышеприведенную формулу, получим:
 .
.
Задача 2. Вычислено следующее уравнение множественной регрессии по сельскохозяйственным предприятиям области, характеризующее связь между размерами предприятия по посевной площади х га, числу коров z шт., доходами предприятия y млн. руб.: y=290+3,12x+0,65z. Требуется проанализировать параметры уравнения регрессии.
Решение. Увеличение посевной площади на один гектар приводит к повышению доходов в среднем на 3,12 млн руб.; увеличение числа коров на 1 голову приводит к повышению доходов на 0,65 млн руб.
Задача 3. по данным задачи №2 получены следующие парные коэффициенты корреляции  .
.
Вычислить коэффициент множественной корреляции и детерминации.
Решение.
 ,
,
 .
.
Таким образом, между доходами, посевной площадью и числом коров существует тесная связь. Коэффициент детерминации в нашем случае равен
 .
.
Это значит, что 70% всей вариации денежных доходов предприятий объясняется действием рассматриваемых факторов.
Задача 4. По данным задачи №3 вычислите коэффициент корреляции между y и x и сделайте выводы.
Решение. Частный коэффициент корреляции характеризует тесноту связи между результативным признаком и одним из факторных при постоянных значениях прочих факторов, т. е.
 ,
,
где  , - парные коэффициенты корреляции. Подставляя в формулу их значения, получим:
, - парные коэффициенты корреляции. Подставляя в формулу их значения, получим:
 .
.
Следовательно, связь между денежными доходами и посевной площадью при исключении влияния других факторов заметная.
Этот же результат можно получить, используя общую формулу коэффициента частной корреляции
 .
.
Подставляя имеющиеся значения, получим:
 .
.
Задача 5. По 10 предприятиям имеются следующие данные, млн руб.(табл.7.1).
Таблица 7.1
| Выпуск продукции | 2,5 | 5,0 | 6,0 | 3,0 | 2,0 | 1,5 | 1,0 | 4,0 | 8,0 | 10,0 |
| Фонд заработной платы | 0,6 | 0,9 | 1,5 | 0,8 | 0,25 | 0,31 | 0,11 | 1,05 | 2,0 | 2,5 |
Определите коэффициент корреляции знаков и сделайте выводы о тесноте связи.
Решение. Для вычисления коэффициента корреляции знаков составим вспомогательную таблицу (табл. 7.2), из которой получим число совпадений знаков от средней. В нашем случае оно равно 8, число несовпадений знаков отклонений от средней - 2.
Таблица 7.2
| № п/п | Выпуск продукции | Фонд з/пл | Знаки отклонения от средней | |
(x- 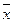 ) )
| (y-  ) )
| |||
| 1,0 | 0,11 | --- | --- | |
| 1,5 | 0,31 | --- | --- | |
| 2,0 | 0,25 | --- | --- | |
| 2,5 | 0,6 | --- | --- | |
| 3,0 | 0,8 | --- | --- | |
| 4,0 | 1,05 | --- | + | |
| 5,0 | 0,9 | + | --- | |
| 6,0 | 1,5 | + | + | |
| 8,0 | 2,0 | + | + | |
| 10,0 | 2,5 | + | + | |
| Итого | 43,0 | 10,0 | ||
| Средняя | 4,3 | 1,0 |
Подставляя эти значения в формулу коэффициента корреляции, получим:
 .
.
Связь между выпуском продукции и фондом заработной платы прямая и заметная.
Задача 6. По 10 предприятиям имеются следующие данные (табл 7.3):
Таблица 7.3
| Среднесписочная численность | ||||||||||
| Выпуск продукции | 5,0 | 4,2 | 6,5 | 8,0 | 10,0 | 1,8 | 6,0 | 2,0 | 9,5 | 11,0 |
Решение. Коэффициент корреляции рангов вычисляется по рангам (порядковым номерам), которые присваиваются всем единицам совокупности, расположенным в порядке возрастания признака. Для его вычисления составим вспомогательную таблицу (табл 7.4).
Таблица 7.4
| №п/п | Выпуск продукции х | Численность работников y | Ранги | Разность рангов d | Квадрат разности рангов 
| |
| по х | по y | |||||
| 5,0 | ||||||
| 4,2 | -1 | |||||
| 6,5 | ||||||
| 8,0 | ||||||
| 10,0 | ||||||
| 1,8 | -1 | |||||
| 6,0 | ||||||
| 2,0 | ||||||
| 9,5 | -2 | |||||
| 11,0 | ||||||
| Итого |
Подставляя соответствующие данные в формулу коэффициента, получим:
 ,
,
то есть связь между выпуском продукции и среднесписочной численностью работников весьма тесная.
Задача 7. По данным табл. 7.5 вычислить коэффициент ассоциации.
Таблица 7.5
Зависимость выполнения плана рабочими от наличия специальной подготовки
| Прошли спецподготовку | Не прошли спецподготовку | Итого | |
| Выполнили план | 70 (а) | 20 (в) | 90 (а+в) |
| Не выполнили план | 2 (с) | 8 (d) | 10 (с+d) |
| Всего | 72 (а+с) | 28 (в+d) |
Решение. Коэффициент ассоциации используется для установления степени тесноты связи между двумя качественными альтернативными признаками, состоящими из двух групп, и определяется по следующей формуле
 .
.
Подставим соответствующие данные из табл. 7.5 в формулу и получим:
 .
.
Как видно, между выполнением плана и наличием специальной подготовки существует прямая и заметная связь.
РАЗДЕЛ 8. РЯДЫ ДИНАМИКИ
8.1. Понятие о динамических рядах и их видах
Процессы и явления общественной жизни, которые изучаются статистикой, находятся в постоянном движении и изменении. В процессе развития меняются размеры, состав, объем, структура конкретных общественных явлений. Эти изменения статистика выражает при помощи различных статистических показателей.
Статистические данные, характеризующие изменения явлений во времени, называются динамическими (хронологическими или временными) рядами. Такие ряды имеют огромное значение для выявления и изучения складывающихся закономерностей в явлениях общественной жизни.
Довольно часто имеющиеся динамические ряды несопоставимы в силу изменения круга объектов учета, территориальных границ, изменения масштаба единиц измерения и т.д. В этом случае для преобразования несопоставимых динамических рядов в сопоставимые используют различные приемы, основные из которых следующие: прямой пересчет данных, пересчеты при помощи ключей и смыкание рядов.
В зависимости от характера изучаемых величин различают три вида динамических рядов:моментные, интервальные и ряды средних.
Моментными рядами называются ряды статистических величин, характеризующие размеры изучаемого явления на определенные даты или моменты времени. Примером могут служить данные о среднесписочной численности работающих по состоянию на первое число каждого месяца.
Отличительной особенностью моментных рядов является то, что они не подлежат суммированию.
Интервальными рядами называются ряды статистических показателей, характеризующих размеры изучаемого явления за определенные промежутки (периоды, интервалы) времени. Интервальные ряды можно суммировать.
Ряды средних величин - это ряды, характеризующие изменения средних уровней изучаемого явления во времени. Как и моментные, ряды средних величин не подлежат суммированию.
Вычисление средней динамического ряда
Средняя, вычисленная из уровней динамического ряда, называется хронологической средней. Способы ее расчета зависят от вида динамического ряда.
a) для интервальных рядов средняя исчисляется по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных - средняя арифметическая взвешенная.
б) для моментных рядов средняя рассчитывается по формуле
 ,
,
т.е. средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.
Если интервалы между периодами неравные, то применяется средняя арифметическая взвешенная, а в качестве весов берутся отрезки времени между датами, к которым относятся парные средние смежных значений уровня.
8.2. Основные показатели, используемые
при анализе динамических рядов
Динамические ряды анализируются при помощи ряда показателей, определяющих характер, направление, интенсивность количественных изменений во времени. К ним относятся:уровень ряда, средний уровень, абсолютный прирост, темп роста, коэффициент роста, темп прироста, коэффициент опережения, абсолютное значение одного процента прироста.
Уровнем ряда называется абсолютная величина каждого члена динамического ряда. Различают начальный (величина первого члена ряда), конечный (последнего), средний уровень ряда.
Средний уровень определяется в зависимости от вида динамического ряда.
Абсолютный прирост характеризует размер увеличения или уменьшения изучаемого явления за определенный период времени. Он определяется как разность между данным уровнем и предыдущим или начальным. Уровень, который сравнивается, называется текущим, а уровень с которым производится сравнение, называется базисным. Если каждый уровень ряда сравнивается с предыдущим, то получаются цепныепоказатели. Если же все уровни ряда сравниваются с одним и тем же, первоначальным уровнем, то полученные показатели называются базисными.
Абсолютный прирост определяется по формулам;
цепной:  ; базисный:
; базисный:  ,
,
где  - текущий уровень ряда;
- текущий уровень ряда;  - уровень предшествующий;
- уровень предшествующий;  - начальный уровень ряда.
- начальный уровень ряда.
Темпом роста называется отношение данного уровня к предыдущему или начальному, выраженному в процентах. Темпы роста бывают цепными и базисными и вычисляются по формулам
цепной:  ; базисный:
; базисный: ;
;
Если темпы роста выражены в виде простых отношений (база-1), то полученные показатели называются коэффициентами роста.
Темпом прироста называется отношение абсолютного прироста к предыдущему или начальному членам ряда, выраженным в процентах;
цепной:  ; базисный
; базисный .
.
Темп прироста также может быть рассчитан как:
цепной: 
 ; базисный
; базисный .
.
Для характеристики темпов роста и прироста в среднем за весь период вычисляют средний темп роста и прироста. Средний темп, коэффициент роста и прироста определяются по формулам средней геометрической.
Для определения средней из средних коэффициентов или темпов роста за неодинаковые промежутки времени применяется средняя геометрическая взвешенная

где m - продолжительность отрезков времени.
Коэффициентом опережения называется отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени
 ,
,
где  -базисные темпы роста первого ряда;
-базисные темпы роста первого ряда;  - базисные темпы роста второго ряда.
- базисные темпы роста второго ряда.
В тех случаях, когда темпы роста по двум сравниваемым рядам динамики неизвестны, а имеются средние темпы роста за одинаковый период времени, коэффициент опережения рассчитывается по формуле
 ,
,
где  - средний темп роста первого ряда динамики,
- средний темп роста первого ряда динамики,  - второго, а n - число лет в периоде.
- второго, а n - число лет в периоде.
Отношение абсолютного прироста к темпу прироста представляет собой абсолютное значение одного процента прироста и определяется по формуле
 ,
,
где A % - абсолютный прирост;  - цепной темп прироста;
- цепной темп прироста;  - уровень, предшествующий
- уровень, предшествующий  .
.
Из формулы видно, что абсолютное значение одного процента прироста равно одной сотой части предшествующего уровня.
8.3. Важнейшие приемы обработки
и анализа динамических рядов
Существуют различные приемы обработки динамических рядов:
а) Приведение рядов к одному основанию.
Для выявления связи или различия в динамике двух или нескольких рядов их можно привести к одному основанию. Для этого показатели каждого ряда выражаются в процентах к первому или любому другому члену ряда.
б) Разбивка ряда на короткие периоды.
Для выявления тенденции данных колеблющихся рядов их разбивают на более короткие периоды, а затем определяют средний уровень по каждому периоду.
в) Сглаживание способом скользящих (подвижных) средних.
Сущность его заключается в том, что по конкретным уровням ряда рассчитываются сглаженные, скользящие средние, которые получаются из подвижных сумм путем последовательного сдвига на одну дату суммируемых показателей. Затем подвижные суммы делят на число дат, получая, таким образом, скользящие или подвижные средние. Например, складывают три первых члена ряда, а их среднюю относят ко второму периоду, затем складывают 2-й, 3-й и 4-й члены ряда, а их среднюю относят к третьему периоду и т.д.
г) Метод аналитического выравнивания динамических рядов.
Сущность метода состоит в том, что основная тенденция выражается в виде функции y=f(x), где за параметр х принимается время t .
8.4. Корреляционный анализ
и сезонные колебания в рядах динамики
Для изучения связи в рядах динамики применяется и корреляционный анализ. Однако его применение связано с определенными трудностями, потому что в динамических рядах уровни независимы друг от друга.
Зависимость между каждым предыдущим и последующим членами динамического ряда называется автокорреляцией. Корреляция между уровнями динамических рядов будет правильно отражать связь между явлениями только при условии устранения автокорреляции. Для этого существует ряд способов.
Первый способ состоит в том, что ищется связь не между уровнями рядов, а между первыми, вторыми и т. д. разностями (т. е. из каждого последующего уровня ряда вычитается значение предыдущего - первые разности и т. д.). В этом случае коэффициент корреляции вычисляется по формуле
 .
.
Второй способ исключения автокорреляции состоит в том, что сопоставляются отклонения от тренда (основной тенденции) по изучаемым рядам: для каждого динамического ряда проводится аналитическое выравнивание, затем находятся отклонения от найденной основной тенденции и уже потом, используя эти отклонения в качестве искомых переменных, определяют связь.
Для многих явлений общественной жизни характерны внутригодичные повторяющиеся колебания, которые называются сезонными. Они наблюдаются в различных отраслях народного хозяйства: при производстве большинства видов сельхозпродуктов, их переработки, в строительстве, транспорте, торговле и т. д.
Для выявления и измерения интенсивности сезонных колебаний пользуются индексами сезонности, причем индексы сезонности могут вычисляться по-разному.
14.Если средний годовой уровень сезонного явления остается от года к году относительно неизменным, применяется метод простых средних. Он состоит в определении простой средней за одни и те же месяцы всего изучаемого периода и в сопоставлении их со средней за весь изучаемый период.
15.Когда уровень явления проявляет тенденцию к росту или снижению, применяют метод помесячных отношений. Он заключается в том, что в начале вычисляются по каждому году процентные отношения между показателями за каждый данный и предшествующий месяцы, а затем из полученных отношений определяется среднеарифметическое.