Решение типовых задач
Задача 1. Проверка пряжи на крепость в лаборатории дала следующие результаты (табл. 5.4):
Таблица 5.4
| Крепость пряжи, г (х) | |||||||
| Количество проб, (f) |
Вычислить все показатели вариации.
Решение. В задаче значения признака имеют различную численность, поэтому значения, 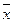 , d,
, d,  ,
,  , Vдолжны вычисляться как средние взвешенные величины. Для вычисления показателей вариации проводим дополнительные расчеты (табл. 5.5)
, Vдолжны вычисляться как средние взвешенные величины. Для вычисления показателей вариации проводим дополнительные расчеты (табл. 5.5)
Таблица 5.5
| x | f | xf | (x - 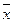 ) )
| (x - 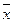 )f )f
| (x - 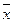 )2 )2
| (x - 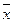 )2f )2f
|
| -29 | -58 | |||||
| -19 | -247 | |||||
| -9 | -216 | |||||
| Итого | +521 -521 |
Средняя крепость пряжи определяется по формуле
 г.
г.
Размах вариации
 г.
г.
Среднее линейное отклонение вычисляется по формуле
 г.
г.
Дисперсия, взвешенная по частоте вариантов, равна
 г2.
г2.
Среднее квадратичное отклонение равно:
 г.
г.
коэффициент вариации составляет
 .
.
Задача 2. На предприятии 64% работников имеют среднее и высшее образование. Определить дисперсию доли рабочих, имеющих среднее и высшее образование.
Решение. Дисперсия альтернативного признака определяется как  =pq,где p – доля единиц совокупности, обладающих данным признаком, а q=1-p – доля единиц совокупности, не обладающих данным признаком, следовательно:
=pq,где p – доля единиц совокупности, обладающих данным признаком, а q=1-p – доля единиц совокупности, не обладающих данным признаком, следовательно:  =0,64·0,36=0,2304.
=0,64·0,36=0,2304.
Задача 3. Имеются следующие данные (табл.5.6):
Таблица 5.6
Заработная плата рабочих по профессиям (1997 год), тыс. руб.
| № п/п | Группы рабочих по профессиям | Число рабочих | З/п одного рабочего в месяц |
| Токари | 140, 160 | ||
| Слесари | 120, 200, 160 | ||
| Кузнецы | 140, 180, 200, 220, 260 |
Вычислить:
среднюю месячную заработную плату для каждой группы и для всех рабочих; групповые дисперсии; среднюю из внутригрупповых дисперсий; межгрупповую дисперсию; общую дисперсию; проверить правило сложения дисперсий и сделать выводы.
Решение. В задаче требуется определить, как влияют на изменение заработной платы рабочих постоянные причины, положенные в основание группировки (в данном случае - различия в профессии), и случайные причины. Для этого необходимо определить систематическую и случайную вариации и их роль в общей вариации. Для решения задачи и вычисления заданных показателей, построим вспомогательную таблицу (табл.5.7).
Таблица 5.7
| № п/п | x | x– 
| 
| 
| 
|
| Токари | |||||
| -10 | -38 | ||||
| -18 | |||||
| Итого: | |||||
| Слесари | |||||
| -40 | -58 | ||||
| -18 | |||||
| Итого: | |||||
| Кузнецы | |||||
| -60 | -38 | ||||
| -20 | |||||
| Итого: | |||||
| Всего: |
Среднюю заработную плату по каждой группе и для всех рабочих определяем по формуле средней арифметической простой:

Внутригрупповые дисперсии вычисляем по формуле:
 Средняя из внутригрупповых дисперсийравна:
Средняя из внутригрупповых дисперсийравна:

Межгрупповая дисперсияопределяется как:
 ,
, 
Общая дисперсия равна: 
По правилу сложения дисперсий общая дисперсия равна сумме средней внутригрупповых и межгрупповой дисперсии: s2 =  2 + d2 = 1140 + 496 = 1636.
2 + d2 = 1140 + 496 = 1636.
Задача 4. Средняя успеваемость студентов экономического факультета  =4 балла, Мо=4,8 балла, Ме=4,2 балла. Указать, симметричным или асимметричным является распределение студентов по успеваемости. Если асимметричным, то с какой асимметрией (левосторонней или правосторонней).
=4 балла, Мо=4,8 балла, Ме=4,2 балла. Указать, симметричным или асимметричным является распределение студентов по успеваемости. Если асимметричным, то с какой асимметрией (левосторонней или правосторонней).
Решение. В симметричном распределении 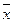 =Мо=Ме. В нашей задаче такого равенства нет. Следовательно, распределение асимметрично, а так как
=Мо=Ме. В нашей задаче такого равенства нет. Следовательно, распределение асимметрично, а так как 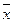 <Ме<Мо, то разности между
<Ме<Мо, то разности между 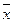 –Ме и
–Ме и 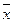 –Мо отрицательные и асимметрия левосторонняя.
–Мо отрицательные и асимметрия левосторонняя.
Задача 5. Урожайность сахарной свеклы в сельхозпредприятиях области характеризуется следующими показателями: 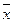 =300 ц/га,
=300 ц/га,  =120 ц/га, Мо=240 ц/га, а урожайность зерновых -
=120 ц/га, Мо=240 ц/га, а урожайность зерновых - 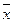 =30ц/га;
=30ц/га;  =10 ц/га, Мо=27 ц/га. Вычислить показатели асимметрии и указать где она больше. Каково направление асимметрии?
=10 ц/га, Мо=27 ц/га. Вычислить показатели асимметрии и указать где она больше. Каково направление асимметрии?
Решение. 
Асимметрия правосторонняя, так как  >0, и больше в первом случае.
>0, и больше в первом случае.
Задача 6. Центральный момент третьего порядка  =34,56 при
=34,56 при  =12. Вычислить коэффициент асимметрии и сделать выводы; центральный момент четвертого порядка
=12. Вычислить коэффициент асимметрии и сделать выводы; центральный момент четвертого порядка  =64,32 при
=64,32 при  =2 . Вычислить коэффициент эксцесса и сделать выводы.
=2 . Вычислить коэффициент эксцесса и сделать выводы.
Решение. 
Асимметрия правосторонняя, так как A>0, и незначительная

Эксцесс выше нормального, потому что E>3.
РАЗДЕЛ 6. ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ
6.1. Общие сведения о выборочном наблюдении
В связи с тем, что статистика имеет дело с массовыми совокупностями статистические исследования весьма трудоемки. Поэтому давно возникла мысль о замене сплошного наблюдения выборочным.
Выборочное наблюдение - это наиболее совершенный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь ее часть, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При проведении выборочного наблюдения нельзя получить абсолютно точные данные. Как при сплошном, так как при выборочном наблюдении неизбежны ошибки, которые делятся на ошибки регистрации и ошибки репрезентативности. В свою очередь, ошибки репрезентативности бывают случайные и систематические.
Важнейшим условием применения выборочного метода является правильный отбор единиц совокупности, а именно:
а) строго объективный отбор единиц совокупности, при котором каждая из них получала бы абсолютно одинаковую возможность попасть в выборку;
б) достаточное количество отобранных единиц совокупности. При соблюдении этих условий выборка будет репрезентативной или представительной.
Вся совокупность единиц, из которой производится отбор, называетсягенеральной совокупностью и обозначается буквойN. Часть генеральной совокупности, попавшая в выборку, называетсявыборочной совокупностью и обозначается n.
Обобщающие показатели генеральной совокупности - средняя, дисперсная и доля - называются генеральнымии соответственно обозначается σ, р, гдеp - доля или отношение числа единиц совокупности М, обладающих данным признаком ко всей численности генеральной совокупности, т.е.
σ, р, гдеp - доля или отношение числа единиц совокупности М, обладающих данным признаком ко всей численности генеральной совокупности, т.е.  . Те же обобщающие характеристики в выборочной совокупности обозначаются соответственно
. Те же обобщающие характеристики в выборочной совокупности обозначаются соответственно  ,
,  2, ω.
2, ω.
Теоретической основой выборочного метода является теорема П.Л.Чебышева, которая формулируется следующим образом: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала:
 < ε .
< ε .
При практическом использовании теоремы Чебышева генеральную дисперсию  , которая неизвестна, заменяют выборочной дисперсией.
, которая неизвестна, заменяют выборочной дисперсией.
6.2. Виды и схемы отбора
Формирование выборочной совокупности из генеральной может осуществляться по-разному. Различают следующие виды отбора: собственно-случайный; механический; типический; серийный; комбинированный.
5. Собственно-случайный отбор. Он ориентирован на выборку единиц из генеральной совокупности без всякого расчленения ее на части или группы. Либо применяется жеребьевка, либо используются таблицы случайных чисел.
6. Механический отбор. Он состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы), причем все единицы генеральной совокупности должны располагаться в определенном порядке. Размер интервала или группы равен обратной величине доли выборки (или количеству отбираемых единиц). Из каждой группы (интервала) берется только одна единица. Так, при 2%-ной выборке отбирается каждая 50-ая единица (1:0,02; или формируется 50 групп или интервалов), при 20%-ной выборке - каждая 5-я единица (1:0,2) и т. д.
7. Типический отбор. При его осуществлении вся генеральная совокупность делится на группы по типическому признаку, а затем в каждой группе проводится тот или иной отбор. Наиболее часто из каждой группы выбирается количество единиц, пропорциональное удельному весу группы в общей совокупности и как правило - механическим отбором. Такой отбор часто называют пропорциональным типическим отбором с механической выборкой.
8. Серийный отбор с равновеликими сериями состоит в выборке не отдельных единиц генеральной совокупности, а целых серий (гнезд). Попавшие в выборку серии подвергаются сплошному наблюдению. Сами серии могут формироваться различными методами и способами.
9. Комбинированный отбор. Все вышеперечисленные виды отбора комбинируются между собой.
Используя различные виды отбора, можно применить и различные схемы отбора: бесповторный отбор (схема невозвращенного шара)- после выбора какой-либо единицы она обратно в генеральную совокупность не попадает и не может быть выбрана снова; повторный отбор (схема возвращенного шара) - после выбора какой-либо единицы она вновь возвращается в генеральную совокупность и может быть выбрана снова.
6.3. Определение средних и предельных ошибок при
различных видах отбора
Ошибка выборки  - разность между характеристиками выборочной и генеральной совокупности.
- разность между характеристиками выборочной и генеральной совокупности.
Если  представляет собой предел, которого не превосходит абсолютная величина
представляет собой предел, которого не превосходит абсолютная величина  то
то 
Ошибка выборки зависит от многих факторов, и, если из одной и той же генеральной совокупности можно сформировать бесконечное множество выборочных совокупностей, каждая из них даст и свою ошибку. Поэтому при выборочном наблюдении говорят о средней из возможных ошибок (средняя или стандартная ошибка выборки), которую обозначают как  .
.
Величина  прямо пропорциональна корню квадратному из дисперсии и обратно пропорциональна квадратному корню из объема выборочной совокупности;
прямо пропорциональна корню квадратному из дисперсии и обратно пропорциональна квадратному корню из объема выборочной совокупности;
 , для доли, соответственно
, для доли, соответственно .
.
Эти формулы справедливы для повторной схемы отбора. При бесповторном отборе вводится поправочный коэффициент, равный
 ,тогда
,тогда  .
.
В тех случаях, когда выборка небольшая этим множителем можно пренебречь, так как его значение близко к единице (обычно при  ).
).
Для решения практических задач важна не средняя ошибка выборки, а пределы, за которые она не выйдет, т.е. говорят о предельной ошибке выборки.
Предельная ошибка выборки связана со средней ошибкой соотношением  , гдеt- коэффициент доверия, илиt- статистика; t принимает значения 1, 2 или 3 и связан с вероятностью достижения заданного предела. Если t=1 это значит, что вероятность того, что ошибка выборки не превысит заданного значения, равна 0,683 или 68,3%. При t=2 - P=0,954 или 95,4%;t=3 - P=0,997 или 99,7%.
, гдеt- коэффициент доверия, илиt- статистика; t принимает значения 1, 2 или 3 и связан с вероятностью достижения заданного предела. Если t=1 это значит, что вероятность того, что ошибка выборки не превысит заданного значения, равна 0,683 или 68,3%. При t=2 - P=0,954 или 95,4%;t=3 - P=0,997 или 99,7%.
Таким образом, предельная ошибка выборки зависит от трех факторов: дисперсии  , объема выборки n, и коэффициента доверияt. Формулы для определения предельных ошибок при различных видах и схемах отбора приведены в табл. 6.1.
, объема выборки n, и коэффициента доверияt. Формулы для определения предельных ошибок при различных видах и схемах отбора приведены в табл. 6.1.
Таблица 6.1
Определение предельной ошибки выборки при различных видах отбора
| Схема отбора | Предельная ошибка выборки | ||||
| для средней | для доли | ||||
| Собственно - случайный и механический отбор | |||||
| Повторный отбор | 
| 
| |||
| Бесповторный отбор | 
| 
| |||
| Типический отбор | |||||
| Поторный отбор |  
| 
| |||
| Бесповторный отбор | 
| 
| |||
| Серийный отбор | |||||
| Повторный отбор | 
| 
| |||
| Бесповторный отбор | 
| 
| |||
6.4. Определение необходимой численности выборки
При разработке выборочного наблюдения предполагают заранее заданными величину допустимой ошибки выборки и вероятность ответа (и t). Неизвестным, следовательно, остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Из формулы  и формул предельных ошибок выборки устанавливаем необходимую численность выборки. Формулы для определения численности выборки n зависят от способа отбора (табл.6.2).
и формул предельных ошибок выборки устанавливаем необходимую численность выборки. Формулы для определения численности выборки n зависят от способа отбора (табл.6.2).
Таблица 6.2
Формулы расчета численности выборки при собственно-случайном отборе
| Способ отбора | Для средней | Для доли | Для доли, если даже приблизительно она неизвестна |
| Повторный | 
| 
| 
|
| Бесповторный |  
| 
| 
|
Численность выборки можно выразить через отношение  , т.е. предельную ошибку выборки выражают в единицах среднего квадратичного отклонения. Так, например, формула численности бесповторной собственно-случайной выборки для средней при t=3 примет вид
, т.е. предельную ошибку выборки выражают в единицах среднего квадратичного отклонения. Так, например, формула численности бесповторной собственно-случайной выборки для средней при t=3 примет вид  .
.
Для типического и серийного отбора объем выборки определяется по специальным формулам.