Доказательство.
1) Имеем 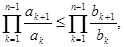 или
или  или
или  или
или
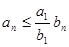 Þ
Þ 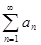 - сходится.
- сходится.
Вторая часть теоремы доказывается аналогично.
Доказано.
Замечание. В обобщённом признаке сравнения выполнение неравенств  достаточно требовать для
достаточно требовать для 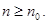
5) Признак Даламбера
Если для ряда 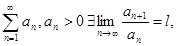 то
то 
Доказательство.Пусть 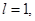 тогда ряд
тогда ряд  сходится,
сходится,  расходится, но
расходится, но 

Пусть  тогда
тогда  и для
и для  сходится и по обобщённому признаку сравнения исходный ряд сходится.
сходится и по обобщённому признаку сравнения исходный ряд сходится.
Пусть 

Значит, ряд расходится.
Доказано.