Основные теоретические сведения
Решение первой задачи:
Приближенное решение уравнений. Точные решения уравнения 
не всегда могут быть найдены. Будем искать действительные значения корней с помощью численных методов при заданной точности.
Решение состоит из двух этапов:
1) отделение корней, т.е. определение отрезков, внутри которых находится только один корень;
2) уточнение корней до заданной степени точности.
Отделение корней можно провести графически или аналитически, т.к. если непрерывная монотонная функция на концах малого отрезка 
принимает значения разных знаков, то внутри этого отрезка содержится корень уравнения . Для решения уравнений, содержащих тригонометрические, логарифмические, показательные функции удобно пользоваться таблицами математических справочников.
Метод половинного деления. Пусть корень уравнения отделен и находится на отрезке . Точка 
– середина отрезка – разбивает его на два равных: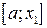 
и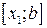 
.
Из этих отрезков выбираем тот, на концах которого функция 
принимает значения разных знаков и так же делим его пополам. Процесс деления пополам продолжается до тех пор, пока не получится отрезок 
, длина которого 
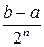меньше заданной точности 
.
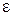Окончательно за приближенное значение корня принимают число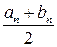 
. Погрешность не превышает 
.
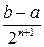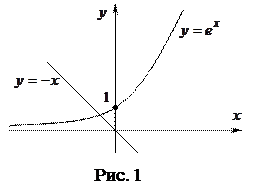Пример. Решить с точностью до 0.01 уравнение 
.
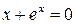Решение. Найдем интервал изоляции корня графически. Уравнение 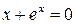запишем в виде 
, где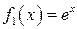 
, 
. Абсцисса точки пересечения графиков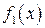 
и 
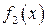– корень уравнения 
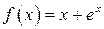, за интервал изоляции возьмем отрезок 
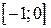(видно по рис. 1).
; 
.
Середина отрезка: 
, 
.
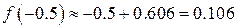Отрезок 
, его середина 
, 
.
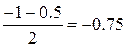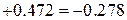Отрезок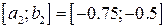 
, середина отрезка 
, 
.
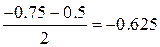Отрезок 
, середина отрезка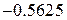 
, 
.
Отрезок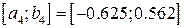 
, середина 
, 
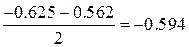и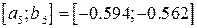 
.
Длина отрезка 
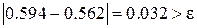, найдем середину отрезка: 
.
Значение функции: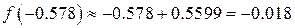 
.
Отрезок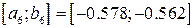 
, середина 
, 
.
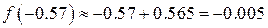, дли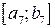на 
равна 
.
За приближенное значение корня берем середину этого отрезка: 
с учетом заданной точности 
.
Способы уточнения корней на отрезке предполагают, что для функции выполняются условия:
1) 
непрерывна на вместе с производными первого и второго порядков;
2) значения на концах отрезка имеют разные знаки, т.е. 
;
3) производные 
и 
сохраняют знак на .
Условия 1 и 2 гарантируют, что на находится хотя бы один корень, а из условия 3 следует, что на данном интервале функция монотонна и поэтому корень будет единственным.
Далее будем предполагать, что условия 1–3 выполняются.
Метод хорд. Метод заключается в многократном процессе замены кривой хорд и отыскания точки пересечения хорды с осью абсцисс (рис. 2).
Пусть корни уравнения отделены и выбран отрезок . Пусть 
– точное значение корня.
Уравнение прямой, проходящей через точку 
и 
(*)
Уравнение оси абсцисс:
. (**)
Точку 
найдем из системы уравнений (*) и (**):
.
Последовательность 
, , 
, … стремиться к искомому корню уравнения .
Вычисления ведутся до тех пор, пока не перестанут изменяться те десятичные знаки, которые нужны для реализации заданной степени точности вычислений.
Оценка погрешности:
,
где – точное значение корня;
– приближенное значение корня.
Пример. Найти один положительный корень уравнения (с точностью до 0.01)
.
Решение. Определим знаки в различных точках:
| 1.5 | 1.8 | 1.9 | |||
|
| – | – | – | – | + | + |
Выберем интервал 
и применим метод хорд:
и 
.
, 
,
следовательно, 
.
.
За значение корня примем 
.
Метод касательных (метод Ньютона). Действительный корень изолирован на отрезке и условие 1 для выполнено.
Возьмем на отрезке такое число 
, что 
. Обычно за берут 
или 
(рис.3).
В точке 
строим касательную. За приближенное значение корня берем абсциссу точки пересечения касательной и оси 
.
Уравнение касательной: 
.
Решая систему 
находим точку 
, где – первое приближение корня 
.
Продолжая этот процесс найдем , 
, …, 
, … Полученная последовательность сходится к искомому корню
, 
Оценка погрешности:
.
Замечание. Несмотря на то, что на каждой итерации объем вычислений в методе касательных больше, чем в методе хорд, т.к. приходится вычислять не только , но и , зато сходимость метода значительно выше. На практике чаще всего применяют комбинированный метод (хорд и касательных).
Комбинированный метод. Ограничения, положенные на функцию , сохраняются:
- – отрезок изоляции корня;
- непрерывна на вместе со своими производными и ;
- для 
;
- и сохраняют знак на .
| 
|
| 
|
|
Если 
, 
или 
, 
, то 
(рис. 4а, 4б).
Если , (рис. 4в) или , (рис. 4г), то 
.
Во всех случаях истинный корень уравнения, заключен между приближенными корнями, получающимися по способу хорд и касательных.
Пример. Найти значение корня положительного уравнения 
с точностью 0.01.
Решение. Найдем интервал изоляции корня графически: 
, корни принадлежат отрезкам 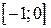и 
.
Проверим 
, 
; при 
, 
; при 
, 
.
Примем за отрезок изоляции отрезок 
.
; 
для любого .
Значение функции 
, поэтому 
.
;
, 
.
Вычислим: 
,
.
Принимаем значение корня 
.
Решение второй задачи рекомендуется проводить по следующей общей схеме.
1. Решить уравнение приближенными методами:
1.1. установить область определения (существования) функции;
1.2. установить, является ли функция четной, нечетной, периодической (специфические особенности функции позволяют сократить объем исследований);
1.3. найти точки разрыва функции, если они существуют, и установить промежутки непрерывности;
1.4. установить поведение функции в окрестностях точек разрыва и наличие у графика функции вертикальных асимптот;
1.5. найти точки пересечения, если они существуют, графика функции с осями координат (методами приближенного вычисления корней);
1.6. установить поведение функции в бесконечности, т.е. при 
и 
(для неограниченной области определения функции);
1.7. установить наличие у графика функции наклонных (в частности, горизонтальных) асимптот и, в случае их существования, найти их.
2. Исследование функции с помощью производных:
2.1. установить промежутки монотонности (возрастания, убывания) функции;
2.2. найти точки внутренних локальных экстремумов (точки максимума, точки минимума), если они существуют, и экстремальные значения функции;
2.3. установить интервалы выпуклости и вогнутости функции, если они существуют;
2.4. найти точки перегиба функции, если они существуют, и значения функции в этих точках, а также угловые коэффициенты касательных к графику в точках перегиба графика функции.
3. Построение (в целом) графика функции.
При выполнении п.1.1 надо воспользоваться определением областью определения функции, заданной аналитически, т.е. формулой (или формулами), называют множество действительных значений аргумента, при которых формула, определяющая функцию, имеет смысл, причем как в процессе всех необходимых вычислений по этой формуле, так и в окончательном результате для функции получаются действительные значения.
При выполнении п.1.2 надо воспользоваться определениями и свойствами:
- четной (нечетной) называют функцию 
, если она определена на симметричном относительно нулевой точки множестве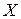 
и для любого 
выполняется равенство 
;
- если функция , четна, то ее график симметричен относительно оси ординат;
- если функция , нечетна, то ее график симметричен относительно начала координат;
- периодической называют функцию , 
, если для нее существует такое положительное число 
(период), что для любого справедливо равенство 
;
- если функция является периодической с периодом , то для построения ее графика достаточно знать ее график на одном из промежутков вида 
; смещая этот график вдоль оси абсцисс на отрезки 
, 
, …, получают график функции .
При выполнении п.1.3 надо воспользоваться определениями и теоремой:
- непрерывна в точке 
, если 
;
- непрерывной в интервале называют функцию, непрерывную в каждой точке этого интервала;
- точками разрыва функции , называют точки, в которых нарушено условие непрерывности:
если 
, то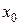 
– точка непрерывности;
если 
, то 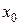– точка разрыва первого рода (точка устранимого разрыва);
если 
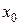, то – точка разрыва первого рода, функция в точке 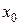имеет скачок 
;
если хотя бы один из пределов 
или 
не существует или равен бесконечности, то в точке 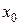функция имеет разрыв второго рода;
Любая элементарная функция непрерывна в каждой точке ее
области определения.
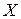При выполнении п.1.4 надо воспользоваться определением: прямую ( – предельная точка ) называют вертикальной (параллельной оси 
) асимптотой графика функции , или
или 
.
При выполнении п.1.5 надо решить уравнения и 
, вещественные корни которых и будут точками на осях и , через которые проходит график функции . Вещественные корни уравнения называют нулями функции.
В простейших случаях область определения функции может быть разбита точками разрыва и нулями функции на определенное число интервалов, в которых сохраняет знак ( 
или 
).
При выполнении п.1.6 надо для , найти пределы 
и 
.
При выполнении п.1.7 надо воспользоваться определениями:
- прямые 
и 
называют наклонными асимптотами графика функции , соответственно при и , если
, 
,
, 
;
- прямые 
и 
называют горизонтальными асимптотами графика функции , соответственно при и , если 
, 
.
При выполнении п.2.1 надо воспользоваться определением и условиями монотонности функции на интервале 
:
- функцию , называют:
· возрастающей на 
, если 
;
· убывающей на , если 
;
· неубывающей на , если 
;
· невозрастающей на , если ( 
);
(функции перечисленных типов называют монотонными на );
- если функция , дифференцируема на , то между характером монотонности функции на и знаком ее производной на этом интервале имеется следующая взаимосвязь:
возрастает;
убывает;
не убывает;
не возрастает;
.
В простейших случаях область определения 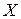функции может быть разбита на определенное число интервалов монотонности критическими точками для функции по первой производной, т.е. точками, в которых 
или не существует (точки, в которых называют точками стационарности функции ).
При выполнении п.2.2 надо воспользоваться определениями, необходимыми и достаточными признаками существования внутреннего локального экстремума (минимума, максимума) функции:
- точку открытого промежутка 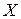называют точкой локального максимума (минимума), а значение функции в ней – локальным максимумом (минимумом) функций , , если у нее существует такая окрестность, для каждой точки которой выполняется неравенство 
;
- если для любой точки ( 
) из этой окрестности имеет место строгое неравенство 
,то точку называют точкой строгого локального максимума (минимума), а значение функции в ней – строгим локальным максимумом (минимумом) функции;
- точки локального максимума и локального минимума называют точками локального экстремума, а значения функции в них – локальными экстремумами функции. На рис.5 изображен график функции , y которой , и 
– точки максимума, , и 
– точки минимума.
Необходимое условие существования экстремума: если – точка экстремума функции , то 
или 
не существует (точки, критические для по первой производной, и только они, являются точками возможного экстремума функции ).
Первое достаточное условие существования экстремума: точка 
является точкой строгого локального экстремума функции , , если выполняются следующие условия
1) непрерывна в , дифференцируема в некоторой ее окрестности за исключением, быть может, самой точки ;
2) при переходе через слева направо меняет знак (при перемене знака с «–» на «+» точка является точкой строгого локального минимума, при перемене знака с «+» на «–» точка является точкой строгого локального максимума (рис.6, 7);
если же при выполнении условия 1 производная при переходе через сохраняет знак, то не является точкой экстремума (рис.8).
Второе достаточное условие существования экстремума: точка является точкой строгого локального экстремума функции , , если
1) имеет в производные до порядка 
( 
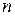) включительно, причем 
, 
;
2) 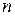– четное; при этом точка является точкой строгого локального минимума, если 
, и точкой строгого локального максимума, если 
;
в частности, является точкой строгого локального минимума функции , , если , 
, и точкой строгого локального максимума, если , 
(рис.9, 10);
- если же при выполнении условия 1 этой теоремы 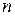является нечетным, то не является точкой экстремума функции.
При выполнении п.2.3 надо воспользоваться определениями и признаками выпуклости (вогнутости), строгой выпуклости (строгой вогнутости) функции на интервале :
- дифференцируемую функцию , называют выпуклой (вогнутой) на , если для любых , 
таких, что , выполняется
;
- дифференцируемую функцию , называют строго выпуклой (строго вогнутой) на , если для любых , таких, что , выполняется
.
График выпуклой на функции лежит не выше любой своей касательной (рис.11).
График вогнутой на функции лежит не ниже любой своей касательной (рис.12).
Для того чтобы дважды дифференцируемая на функция , была выпуклой (вогнутой) на , необходимо и достаточно, чтобы на этом интервале
;
Для того чтобы дважды дифференцируемая на функция , была строго выпуклой (строго вогнутой) на , достаточно, чтобы на этом интервале
.
В простейших случаях область определения 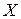функции может быть разбита на определенное число интервалов выпуклости и вогнутости функции критическими точками для функции по второй производной, т.е. точками, в которых 
или не существует (точки, в которых , называют точками стационарности функции ).
При выполнении п.2.4 надо воспользоваться определением, необходимым и достаточными признаками существования у функции точки перегиба:
- точку называют точкой перегиба функции , , если в ней функция имеет конечную либо бесконечную производную и эта точка отделяет интервал строгой выпуклости функции от интервала строгой вогнутости;
- если – точка перегиба функции , то в этом случае точку 
называют точкой перегиба графика функции, т.е. график функции в точке «перегибается» через касательную к нему в этой точке, переходит с одной стороны касательной на другую (рис.13, 14);
- если – точка перегиба функции , то или не существует (точки перегиба отыскиваются среди точек, в которых или не существует, т.е. среди критических точек для функции по второй производной);
- точка является точкой перегиба функции , , если
1) дифференцируема в , дважды дифференцируема в некоторой ее окрестности за исключением, быть может, самой точки ;
2) меняет знак при переходе через ;
- если же при выполнении условия 1 вторая производная при переходе через сохраняет знак, то не является точкой перегиба;
- точка является точкой перегиба функции , , если
1) имеет в производные до порядка 
включительно, причем 
, ;
2) 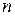– нечетное;
в частности, является точкой перегиба функции , , если 
, 
;
- если же при выполнении условия 1 этой теоремы 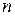является четным, то не является точкой перегиба функции.
Выполнение пп.1, 2 рекомендуется сопровождать постепенным построением графика функции.
Характерные точки – точки пересечения графика функции с осями координат, точки экстремума, точки перегиба графика функции – используются при построении графика функции в качестве «опорных» точек.
При выполнении п.3 в целях уточнения графика функции, если в этом есть необходимость, находят дополнительно отдельные точки графика.
При построении графиков функций полезно также иметь в виду, что, зная график функции , можно построить графики функций:
– зеркальным отражением графика функции относительно оси абсцисс;
– зеркальным отражением графика функции относительно оси ординат;
– часть графика , где 
остается неизменной, часть графика, лежащую ниже оси абсцисс, т.е. при 
, отображается в верхнюю полуплоскость симметрично оси абсцисс;
– график функции для 
отображается на левую полуплоскость, симметрично оси ординат;
– параллельным переносом графика функции на расстояние, равное 
в положительном направлении оси ординат при 
и в отрицательном – при 
;
– параллельным переносом графика функции на расстояние, равное 
, в положительном направлении оси абсцисс при 
и в отрицательном – при 
;
– «растяжением» 
в 
раз (при 
сжатием в 
раз) графика функции относительно оси ординат;
– «сжатием» графика относительно оси абсцисс в раз («растяжением» относительно оси абсцисс в раз графика функции при ).
Решение третьей задачи рекомендуется проводить по схеме:
1) найти все критические по первой производной точки для заданной непрерывной функции на интервале ;
2) найти значения функции в этих критических точках и в граничных точках и 
.
Наибольшее (наименьшее) из этих значений и будет наибольшим (наименьшим) значением функции на отрезке 
.
Если непрерывная функция имеет на отрезке лишь одну точку локального максимума (или лишь одну точку локального минимума), то это значение является наибольшим (соответственно наименьшим) значением на отрезке .
Если функция на отрезке монотонна, то наибольшее и наименьшее значения функция достигает в граничных точках.
Отметим, что функция, непрерывная на отрезке, хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной точке – наименьшее.
При решении четвертой задачи рекомендуется представить , в виде 
и воспользоваться приближенным равенством 
при малых 
, т.е.
или 
.
Эта формула позволяет приближенно найти значение 
при малом , если вычислены 
и – значения функции и ее производной в точке . При этом погрешность 
тем меньше, чем меньше . Эта погрешность при 
является бесконечно малой более высокого порядка, чем .
При решении пятой задачи рекомендуется воспользоваться определением полинома Тейлора и его свойствами:
- полиномом Тейлора степени 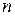функции , в точке называют многочлен
,
где 
– конечные производные;
- значение полинома Тейлора 
и его производных в точке совпадают со значениями функции и ее производных точке ;
- полином Тейлора обладает свойством наилучшей локальной аппроксимации, т.е. в достаточно малой окрестности точки имеет место неравенство
, ,
где 
– любой полином, степени не выше 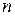отличный от ;
- имеет место приближенное равенство 
при малых 
; при этом погрешность 
тем меньше, чем меньше . Эта погрешность при 
является бесконечно малой более высокого порядка, чем 
;
в частности, при 
и 
;
.
При этом погрешности 
и 
являются при бесконечно малыми более высокого порядка, чем соответственно и 
.
Геометрически полином Тейлора первой степени 
представляет собой касательную к графику функции в точке , а полином Тейлора второй степени 
представляет собой параболу, проходящую через точку и имеющую в этой точке общую касательную с графиком функции и одинаковую с ним кривизну 
и, следовательно, одинаковый радиус кривизны 
.
Типовой вариант и его решение
Задача 1. Комбинированным методом хорд и касательных найти один из корней уравнения 
с точностью до 0. 01.
Решение. Произведем дополнительные вычисления:
, 
.
Отделим корни аналитически. Определим интервалы возрастания и убывания функции: при 
, т.е. 
, 
.
Все данные запишем в таблицу знаков функции .
Таблица 1