Виды неопределенностей
.
!!! Основной задачей при вычислении пределов является устранение неопределенностей с помощью алгебраических преобразований.
1) для неопределенности вида 
:
- Если в числителе и знаменателе сложные степенные или показательные функции и 
. Вычисление пределов в случае отношения степенных функций производится путем вынесения за скобку в числителе и знаменателе дроби переменной x в наибольшей степени среди всех слагаемых дроби (неопределенность устраняется после сокращения дроби и применения основных теорем о пределах); в случае показательных функций за скобку выносится наибольшее слагаемое.
- Правило Лопиталя: Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле, т.е.
.
2) для неопределенности вида 
:
- Если возможно, то числитель и знаменатель разложить на множители. Неопределенность устраняется после сокращения дроби.
- Числитель и знаменатель дроби домножить на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.
Формулы сокращенного умножения:
(a-b)(a+b)= a2-b2
(a-b)(a2+ab+b2)=a3-b3
- Правило Лопиталя.
3) для неопределенности вида [0 
]:
- Выражение, представляющее собой произведение функций, нужно преобразовать в частное (не меняя смысла). После чего неопределенность преобразуется к виду или .
4) для неопределенности вида [ 
]:
- Если функция, стоящая под знаком предела, представляет собой сумму или разность дробей, то неопределенность или устраняется, или приводится к типу после приведения к общему знаменателю.
- Если функция, стоящая под знаком предела, представляет собой разность или сумму иррациональных выражений, то неопределенность или устраняется, или приводится к типу путем домножения и деления функции на одно и то же выражение, приводящее к формулам сокращенного умножения.
5) для неопределенности вида [ 
]:
- Выражение, стоящее под знаком предела представляет собой степенно-показательную функцию (в основании которой необходимо выделить целую часть дроби). Неопределенность устраняется при помощи выделения второго замечательного предела.
Формула второго замечательного предела:
;
.
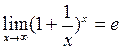120. Необходимые и достаточные условия
монотонности функции. Экстремумы функции
Определение 1. Точка 
называется точкой максимума функции 
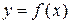, если существует такая 
-окрестность точки , что для всех 
из этой окрестности выполняется неравенство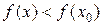 
.
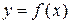Определение 2. Точка называется точкой минимума функции , если существует такая -окрестность точки , что для всех из этой окрестности выполняется неравенство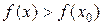 
.
Определение 3.Экстремумом функции 
называется точка максимума или минимума функции.
Определение 4.Функция называется возрастающей на множестве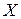 
, если для любых значений 
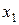и 
из области определения: 
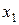, и убывающей, если для любых значений и из области определения: 
.
Теорема 1 (необходимое условие монотонности функции на отрезке).Пусть функция непрерывна на отрезке 
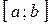и дифференцируема на интервале 
. Тогда:
1) если функция монотонно возрастает на интервале , то 
на ;
2) если функция монотонно убывает на интервале , то 
на .
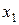Доказательство. Пусть функция монотонно возрастает на интервале . Тогда для любых значений и из интервала имеем: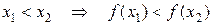 
.
Возьмем произвольную точку 
, придадим аргументу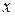 
приращение 
так, что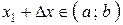 
, функция получит приращение 
: 
.
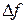Отсюда получаем:
1) если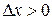 
, то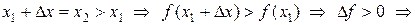 
;
2) если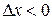 
, то 
.
Таким образом, на интервале .
Доказательство п. 2) проводится аналогично.
Теорема 2 (достаточное условие монотонности функции на отрезке). Пусть функция непрерывна на отрезке 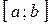и дифференцируема на интервале . Тогда, если для любой точки 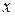интервала , то функция – возрастающая на интервале и если , то – убывающая на интервале функция.
Доказательство. Т.к. функция непрерывна на отрезке 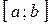и дифференцируема на интервале , то выполняются теоремы Ферма, Ролля и Лагранжа. Рассмотрим точки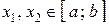 
. Пусть 
. Тогда, по теореме Лагранжа, существует точка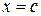 
, причем 
:
.
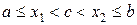1) Если для любого 
, следовательно, функция возрастает на отрезке .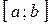
2) Если для любого 
, следовательно, функция убывает на отрезке .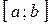
Теорема 3.Для того, чтобы функция , непрерывная на отрезке 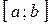и дифференцируемая на интервале , была постоянной функцией, необходимо и достаточно, чтобы ее производная на данном интервале была равна нулю.
Доказательство. 1) Необходимость.
Пусть 
для любого 
. Тогда для любого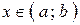 
.
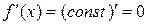2) Достаточность.
Пусть для любого 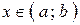выполняется 
.
Выберем два любых 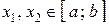: . Тогда по теореме Лагранжа существует 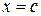, где :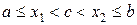
по предположению, следовательно, 
– постоянная функция на .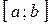
Теорема 4 (первое достаточное условие существования экстремума). Пусть функция – дифференцируемая функция.
1) Если в точке первая производная 
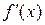меняет свой знак с “+” на “–”, то функция имеет в точке максимум.
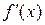2) Если в точке первая производная меняет свой знак с “–” на “+”, то функция имеет в точке минимум.
Доказательство. Доказательство следует из необходимого и достаточного условия монотонности функции.
Теорема 5 (второе достаточное условие существования экстремума).Пусть функция дважды дифференцируема, причем 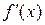и 
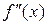– непрерывные функции. Тогда:
1) если 
и 
– точка максимума функции ;
2) если и 
– точка минимума функции .
Доказательство.
1) Пусть и 
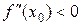. В силу своей непрерывности функция 
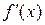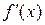в некоторой окрестности точки . Тогда по теореме 2 функция убывает в этой окрестности. Поскольку , то функция меняет в точке свой знак с “+” на “–”. Следовательно, по теореме 4 функция имеет в точке максимум.
2) Пусть и 
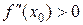. В силу своей непрерывности функция 
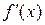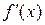в некоторой окрестности точки . Тогда по теореме 2 функция возрастает в этой окрестности. Поскольку , то функция меняет в точке свой знак с “–” на “+”. Следовательно, по теореме 4 функция имеет в точке минимум.
Теорема 6 (необходимое условие существования экстремума функции в точке).Пусть функция имеет в точке экстремум. Тогда производная 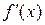либо равна нулю в точке , либо не существует.
Доказательство. Если в точке функция достигает экстремума, скажем максимума, то значение функции в этой точке является наибольшим ее значением в некоторой окрестности точки . Но по теореме Ферма в тех внутренних точках интервала, в которых дифференцируемая функция достигает своего наибольшего значения, ее производная равна нулю. Аналогично проводится рассуждение и для точки минимума.
130. Наибольшее и наименьшее значения функции на отрезке
Определение. Критическими точками 1-го порядка функции 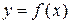называют точки, в которых первая производная или не существует.
Теорема. Пусть функция 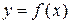определена и непрерывна на отрезке 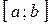. Тогда она достигает своего наибольшего и наименьшего значений на этом отрезке либо в критических точках 1-го порядка, либо на концах отрезка.
Пример. Дана функция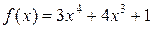 
. Найти ее наименьшее и наибольшее значения на отрезке 
.
Решение. Найдем критические точки. Для этого найдем производную и приравняем ее к нулю:
;
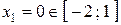при 
и при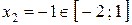 
. Находим: 
, 
, 
, 
.
Таким образом, 
при 
, 
при 
.
140. Выпуклость и вогнутость функции
Определение 1. Функция называется выпуклой в точке , если в окрестности этой точки график этой функции лежит по одну сторону от касательной, построенной к графику функции в точке .
Определение 2.Функция называется выпуклой вверх или просто выпуклой, если ее график в окрестности точки лежит ниже касательной, построенной к графику в точке по отношению к оси 
.
Определение 3. Функция называется выпуклой вниз или вогнутой, если ее график в окрестности точки лежит выше касательной, построенной к графику в точке по отношению к оси .