Производная функции одной переменной
10. Задачи, приводящие к понятию производной.
Задача о скорости движущейся точки
Пусть s = s (t) представляет закон прямолинейного движения материальной точки.
Это уравнение выражает путь s, пройденный точкой, как функцию времени t.
Обозначим через Δs путь, пройденный за промежуток времени Δt от момента t до t + Δt , т. е.
Δs = s(t + Δt ) - s (t). Отношение  называется средней скоростью точки за время от t до t + Δt.
называется средней скоростью точки за время от t до t + Δt.
Чем меньше Δt, т. е. чем короче промежуток времени от t до t + Δt, тем лучше средняя скорость характеризует движение точки в момент времени t. Поэтому естественно ввести понятие скорости v в данный момент t, определив ее как предел средней скорости за промежуток отt до t + Δt, когда Δt→ 0: 
Величина v называется мгновенной скоростью точки в данный момент t.
Задача о касательной к данной кривой.
Пусть на плоскости хОу дана кривая уравнением у = f (х). Требуется провести касательную к данной кривой в данной точке  .
.
Так как точка касания  дана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. tg φ — тангенс угла наклона касательной к положительному направлению оси Ох (рис.16).
дана, то для решения задачи потребуется найти только угловой коэффициент искомой касательной, т. е. tg φ — тангенс угла наклона касательной к положительному направлению оси Ох (рис.16).
 Рис.16
Рис.16
Через точки  и
и  проведем секущую
проведем секущую 
Из рис. видно, что угловой коэффициент tg α секущей  равен отношению
равен отношению  — , где
— , где
 Угловой коэффициент касательной
Угловой коэффициент касательной  к данной кривой в точке
к данной кривой в точке  можно найти на основании следующего определения:
можно найти на основании следующего определения:
Определение 1.Касательной к кривой в точке  называется прямая
называется прямая  , угловой коэффициент которой равен пределу углового коэффициента секущей
, угловой коэффициент которой равен пределу углового коэффициента секущей  , когда
, когда  . Отсюда следует, что
. Отсюда следует, что

Определение 2.Производной функции  называется предел отношения приращения функции к приращению независимой переменной при произвольном стремлении этого приращения к нулю:
называется предел отношения приращения функции к приращению независимой переменной при произвольном стремлении этого приращения к нулю:
 .
.
Значение производной функции в какой-либо данной точке  обозначается обычно
обозначается обычно  или
или  .
.
Геометрический смысл производной. Значение производной  равно угловому коэффициенту касательной к графику функции
равно угловому коэффициенту касательной к графику функции 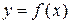 в точке с абсциссой
в точке с абсциссой  .
.
Механический смысл производной. Пусть задан путь s = s (t) движения материальной точки. Скорость данной материальной точки в момент времени t есть производная от пути s по времени t: v(t)= 
Теорема (необходимое условие дифференцируемости). Пусть функция  определена в точке
определена в точке  и некоторой ее окрестности
и некоторой ее окрестности  и дифференцируема в этой точке (т.е. имеет производную). Тогда функция
и дифференцируема в этой точке (т.е. имеет производную). Тогда функция  непрерывна в этой точке.
непрерывна в этой точке.
 Доказательство.
Доказательство.  , следовательно,
, следовательно,  непрерывна в точке
непрерывна в точке  .
.
20. Основные свойства производной
Теорема 1.Пусть функции  ,
,  дифференцируемы. Тогда функция
дифференцируемы. Тогда функция  будет дифференцируема и
будет дифференцируема и
 .
.
Доказательство.



 .
.
Теорема 2. Пусть функции  ,
,  дифференцируемы. Тогда функция
дифференцируемы. Тогда функция  будет дифференцируема и
будет дифференцируема и
 .
.
Доказательство.




 .
.
Теорема 3. Пусть функции  ,
,  дифференцируемы. Тогда функция
дифференцируемы. Тогда функция  будет дифференцируема (там, где она существует) и
будет дифференцируема (там, где она существует) и
 .
.
Доказательство.




 .
.
30. Производная сложной функции
Теорема. Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности  и дифференцируема в точке
и дифференцируема в точке  ; функция
; функция  определена в точке
определена в точке  :
:  некоторой окрестности
некоторой окрестности  и дифференцируема в точке
и дифференцируема в точке  . Тогда
. Тогда  будет дифференцируема в точке
будет дифференцируема в точке  , причем
, причем
 .
.
Доказательство. Дадим  приращение
приращение  . Тогда
. Тогда  и
и  получат соответственно приращения
получат соответственно приращения  и
и  .
.
Предположим, что  при
при  не принимает значений, равных нулю. Тогда рассмотрим:
не принимает значений, равных нулю. Тогда рассмотрим:
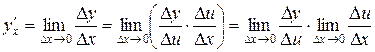 .
.
Т.к. функция  дифференцируема в точке
дифференцируема в точке  , а, следовательно, и непрерывна в точке
, а, следовательно, и непрерывна в точке  , то при
, то при 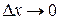 также и
также и  . Следовательно,
. Следовательно,

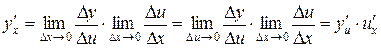 .
.
Замечание. Теорема остается справедливой и в случае, если  будет обращаться в нуль.
будет обращаться в нуль.
Пример. Найти производную функции 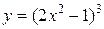 .
.
Решение.
 .
.
40. Производная обратной функции
Теорема. Пусть функция 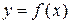 определена в точке
определена в точке  и некоторой ее окрестности и монотонна в этой окрестности (т.е. либо возрастает, либо убывает). Тогда, если функция
и некоторой ее окрестности и монотонна в этой окрестности (т.е. либо возрастает, либо убывает). Тогда, если функция 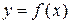 дифференцируема в точке
дифференцируема в точке  , то обратная функция
, то обратная функция  будет дифференцируема в точке
будет дифференцируема в точке 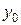 :
: 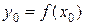 и производная обратной функции:
и производная обратной функции:
 .
.
Доказательство. Рассмотрим точку  и значение функции
и значение функции 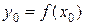 . Рассмотрим точку
. Рассмотрим точку 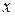 из окрестности точки
из окрестности точки  и
и 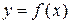 .
. 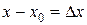 – приращение аргумента, тогда
– приращение аргумента, тогда  будет меняться:
будет меняться: 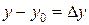 .
.


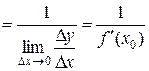 .
.
Замечание. Если  , то теорема в этом случае не работает.
, то теорема в этом случае не работает.
50. Уравнения касательной и нормали к линии
 Составим уравнение касательной к линии
Составим уравнение касательной к линии  , являющейся графиком функции
, являющейся графиком функции 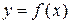 в ее точке
в ее точке 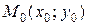 , где
, где 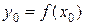 (рис. 17). Т.к. касательная проходит через точку
(рис. 17). Т.к. касательная проходит через точку 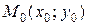 и имеет угловой коэффициент, равный
и имеет угловой коэффициент, равный  , то ее уравнение имеет вид
, то ее уравнение имеет вид
 . (1)
. (1)
Определение.Нормалью к линии в ее точке 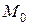 называется прямая, проходящая через точку
называется прямая, проходящая через точку 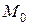 перпендикулярно касательной данной линии, построенной в точке
перпендикулярно касательной данной линии, построенной в точке 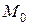 .
.
Т.к. нормаль к линии  в точке
в точке 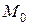 проходит через точку
проходит через точку 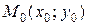 и имеет угловой коэффициент, равный
и имеет угловой коэффициент, равный  , то ее уравнение имеет вид
, то ее уравнение имеет вид
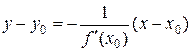 . (2)
. (2)
60. Дифференцирование элементарных функций
1.  –
–  :
: 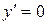 .
.
 Доказательство.
Доказательство. 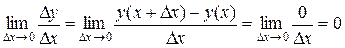 .
.
2.  :
: 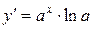 .
.
Доказательство.
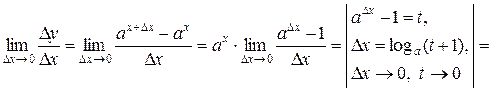
 .
.
(*): 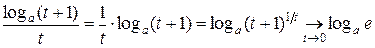 .
.
 Таким образом,
Таким образом,  .
.
3.  :
:  (частный случай п.2).
(частный случай п.2).
4.  :
: 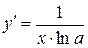 .
.
Доказательство.

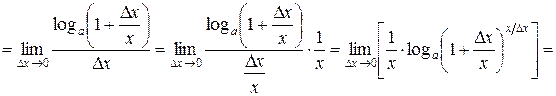
 .
.
 Таким образом,
Таким образом,  .
.
5. 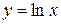 :
:  (частный случай п.4).
(частный случай п.4).
6.  :
: 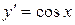 .
.
Доказательство.

 .
.
 Таким образом,
Таким образом, 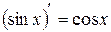 .
.
7.  :
: 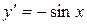 .
.
Доказательство.

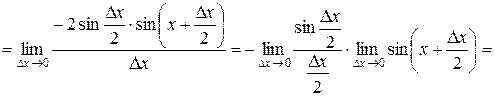
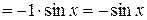 .
.
 Таким образом,
Таким образом,  .
.
8.  :
: 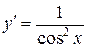 .
.
Доказательство.

 .
.
 Таким образом,
Таким образом,  .
.
9.  :
:  .
.
Доказательство.

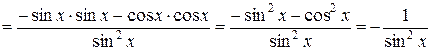 .
.
 Таким образом,
Таким образом, 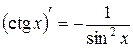 .
.
10. 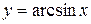 :
: 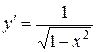 .
.
Доказательство. Пусть 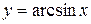 , тогда
, тогда 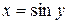 – обратная функция. Отсюда
– обратная функция. Отсюда  . Следовательно, по теореме о производной обратной функции:
. Следовательно, по теореме о производной обратной функции:
 .
.
 Таким образом,
Таким образом,  .
.
Замечание. Корень берется со знаком “+”, потому что значения функции 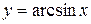 лежат в интервале
лежат в интервале  , а
, а 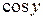 в этом интервале положителен. При
в этом интервале положителен. При 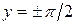 , т.е. для
, т.е. для  производной не существует, хотя сама функция
производной не существует, хотя сама функция 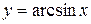 в этих точках определена.
в этих точках определена.
11.  :
:  .
.
Доказательство. Пусть  , тогда
, тогда 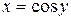 – обратная функция. Следовательно:
– обратная функция. Следовательно:
 .
.
 Таким образом,
Таким образом,  .
.
12. 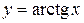 :
:  .
.
Доказательство. Пусть 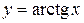 , тогда
, тогда 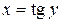 – обратная функция. Следовательно:
– обратная функция. Следовательно:
 .
.
 Таким образом,
Таким образом, 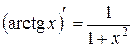 .
.
13. 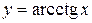 :
: 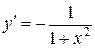 .
.
Доказательство. Пусть 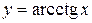 , тогда
, тогда  – обратная функция. Следовательно:
– обратная функция. Следовательно:
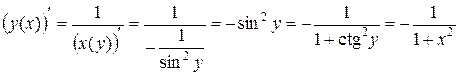 .
.
 Таким образом,
Таким образом,  .
.
14.  :
:  .
.
Доказательство. Пусть  , тогда
, тогда 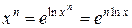 . Следовательно:
. Следовательно:
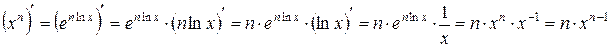 .
.
 Таким образом,
Таким образом, 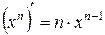 .
.
70. Производная степенно-показательной функции
Определение. Функция вида
 ,
,  ,
,
где и основание, и показатель изменяются вместе с независимой переменной, называется степенно-показательной.
Найдем ее производную 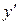 .
.
1) Прологарифмируем данную функцию:
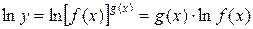 .
.
2) Продифференцируем полученное тождество. С одной стороны:
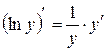 .
.
С другой стороны:
 .
.
Следовательно:

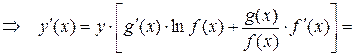
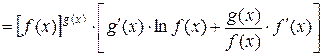 .
.
Операция, состоящая в последовательном применении к функции  сначала логарифмирования (по основанию
сначала логарифмирования (по основанию  ), а затем дифференцирования, называется логарифмическим дифференцированием, а ее результат
), а затем дифференцирования, называется логарифмическим дифференцированием, а ее результат

– логарифмической производной от функции  .
.
Пример. 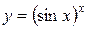 . Найти
. Найти 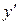 .
.
Решение.
1) 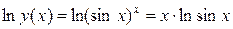 .
.
2) С одной стороны: 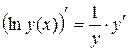 ;
;
С другой стороны: 
 .
.
Следовательно,  .
.
80. Дифференцирование неявной функции
Определение. Неявной функцией  независимой переменной
независимой переменной  называется функция, значения которой находятся из уравнения, связывающего
называется функция, значения которой находятся из уравнения, связывающего  и
и  и не разрешенного относительно
и не разрешенного относительно  .
.
Уравнение функции, заданной неявно, имеет вид
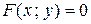 . (3)
. (3)
Пусть функция задана неявно уравнением (3). Тогда производную от этой функции можно найти, дифференцируя по  обе части уравнения с учетом того, что
обе части уравнения с учетом того, что  есть функция от
есть функция от  (определяемая этим уравнением).
(определяемая этим уравнением).
Пример. Дана функция 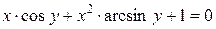 . Найти
. Найти  .
.
Решение. Функция задана неявно. Дифференцируем обе части уравнения по 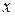 :
:
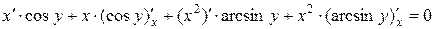 ,
,
 ,
,
отсюда 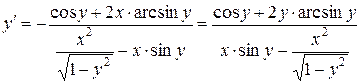 .
.
90. Производные высших порядков
Допустим, что функция 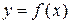 имеет производную
имеет производную 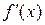 в некотором интервале независимой переменной
в некотором интервале независимой переменной 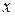 . Производная от
. Производная от 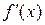 (если она существует) называется производной второго порядка или второй производной от первоначальной функции
(если она существует) называется производной второго порядка или второй производной от первоначальной функции  и обозначается
и обозначается 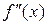 :
:
 .
.
Таким же образом производной третьего порядка или третьей производной  от функции
от функции 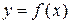 называется производная от производной второго порядка.
называется производная от производной второго порядка.
Определение. Производной  -го порядка
-го порядка 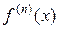 называется производная от производной
называется производная от производной  -го порядка
-го порядка
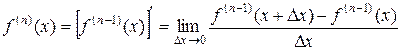 .
.
Все свойства, которые имеют место для первой производной функции, сохраняются и для второй производной и для производной  -го порядка.
-го порядка.
Пример.
 ,
,  ,
,  , …,
, …,
 .
.
100. Основные теоремы для дифференцируемых функций
Теорема Ферма. Если функция  непрерывна на отрезке
непрерывна на отрезке 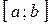 и достигает своего наибольшего или наименьшего значения во внутренней точке
и достигает своего наибольшего или наименьшего значения во внутренней точке 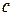 этого отрезка (т.е.
этого отрезка (т.е.  ), то, если в точке
), то, если в точке 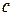 существует производная
существует производная 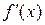 , то она обязательно равна 0:
, то она обязательно равна 0: 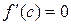 .
.
Доказательство. Предположим, что функция  непрерывна на отрезке
непрерывна на отрезке 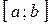 и достигает своего наибольшего значения в точке
и достигает своего наибольшего значения в точке  , которая является внутренней точкой отрезка
, которая является внутренней точкой отрезка 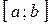 . Пусть функция
. Пусть функция  дифференцируема в точке
дифференцируема в точке  . Покажем, что
. Покажем, что 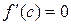 . Действительно:
. Действительно:
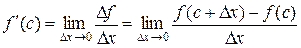 .
.
Существование 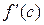 означает, что в точке
означает, что в точке 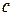 существуют оба односторонних предела функции
существуют оба односторонних предела функции  , которые равны между собой. Рассмотрим эти пределы:
, которые равны между собой. Рассмотрим эти пределы:
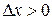 :
: 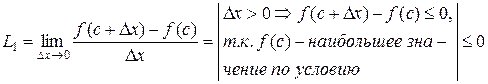 ; (4)
; (4)
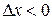 :
:  . (5)
. (5)

 . Из результатов (3) и (4) следует, что
. Из результатов (3) и (4) следует, что 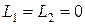 , следовательно,
, следовательно, 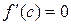 .
.
Геометрический смысл.
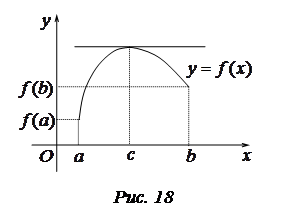
Касательная будет параллельна оси  – геометрическое истолкование теоремы Ферма (рис. 18).
– геометрическое истолкование теоремы Ферма (рис. 18).
Теорема Ролля. Если функция  непрерывна на отрезке
непрерывна на отрезке 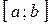 и дифференцируема на интервале
и дифференцируема на интервале  и при этом
и при этом 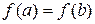 , т.е. принимает одинаковые значения на концах отрезка, то существует по крайней мере одна точка
, т.е. принимает одинаковые значения на концах отрезка, то существует по крайней мере одна точка  такая, что
такая, что 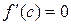 .
.
Доказательство. Рассмотрим два случая.
1) 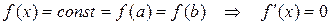 для любого
для любого 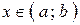 ;
;
 2)
2) 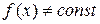 , тогда по свойству непрерывных функций
, тогда по свойству непрерывных функций  достигает своего наибольшего и наименьшего значений на отрезке
достигает своего наибольшего и наименьшего значений на отрезке 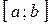 . Тогда хотя бы одно из этих значений достигается во внутренней точке отрезка
. Тогда хотя бы одно из этих значений достигается во внутренней точке отрезка 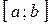 . Обозначим эту точку через
. Обозначим эту точку через 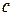 :
:  . Функция
. Функция  дифференцируема на всем интервале
дифференцируема на всем интервале  , а значит и в точке
, а значит и в точке 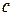 . Следовательно, по теореме Ферма,
. Следовательно, по теореме Ферма, 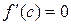 .
.
Геометрический смысл
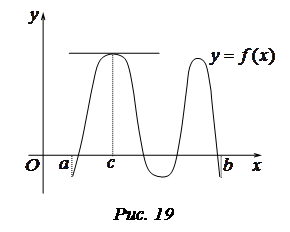 Если на концах отрезка функция
Если на концах отрезка функция  дифференцируема и принимает одинаковые значения, то найдется хотя бы одна точка, где касательная параллельна оси
дифференцируема и принимает одинаковые значения, то найдется хотя бы одна точка, где касательная параллельна оси  – геометрическое истолкование теоремы Роля (рис. 19).
– геометрическое истолкование теоремы Роля (рис. 19).
Теорема Лагранжа. Пусть функция  непрерывна на отрезке
непрерывна на отрезке 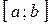 и дифференцируема на интервале
и дифференцируема на интервале  , тогда существует такая точка
, тогда существует такая точка  , что
, что
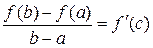 .
.
Доказательство.
Рассмотрим функцию  , которая, очевидно, непрерывна на отрезке
, которая, очевидно, непрерывна на отрезке 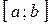 и дифференцируема на интервале
и дифференцируема на интервале  . Рассмотрим, какие значения функция принимает на концах отрезка.
. Рассмотрим, какие значения функция принимает на концах отрезка.
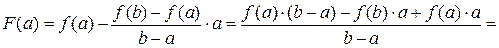
 .
.
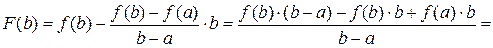
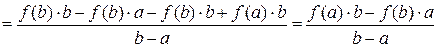 .
.
Получили  , следовательно, функция
, следовательно, функция  удовлетворяет условиям теоремы Ролля. По теореме Ролля, существует точка
удовлетворяет условиям теоремы Ролля. По теореме Ролля, существует точка  :
: 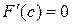 . Имеем:
. Имеем:
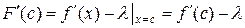 .
.

 .
.
Геометрический смысл.

На отрезке 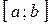 найдется хотя бы одна точка, в которой касательная к кривой
найдется хотя бы одна точка, в которой касательная к кривой 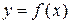 будет параллельна хорде, стягивающей концы дуги кривой (
будет параллельна хорде, стягивающей концы дуги кривой ( 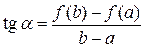 – тангенс угла наклона хорды, которая стягивает концы кривой) (рис. 20).
– тангенс угла наклона хорды, которая стягивает концы кривой) (рис. 20).
110. Правило Лопиталя раскрытия неопределенностей.Раскрытие неопределенностей различных видов.
ОпределениеПравило Лопиталя представляет собой метод вычисления пределов, имеющих неопределенность
типа 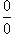 или
или  .
.
Пусть a является некоторым конечным действительным числом или равно бесконечности.
· Если  и
и 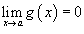 , то
, то 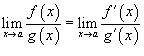 ;
;
· Если  и
и 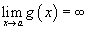 , то аналогично
, то аналогично 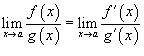 .
.
Пример. Вычислить предел, используя правило Лопиталя 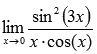
Решение. Подставляем значение
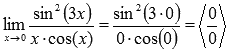
Пределы с неопределенностью данного типа можно находить по правилу Лопиталя:
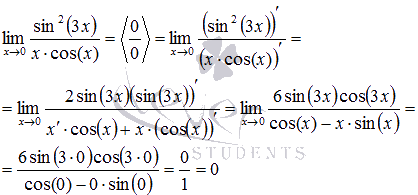
Пример. Найти предел 
Решение. Подставляем бесконечность

Для данного типа неопределенностей можно использовать правило Лопиталя при нахождении предела.
