Определение предела функции по Коши
Пусть  и
и  - предельная точка множества
- предельная точка множества  . Вектор
. Вектор  называется пределом функции
называется пределом функции  при
при  , если для любой окрестности
, если для любой окрестности 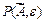 вектора
вектора  существует такая проколотая окрестность
существует такая проколотая окрестность 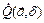 точки
точки  , что как только
, что как только  , тотчас
, тотчас  .
.
Используя понятие окрестности, данное определение может быть сформулировано в следующем виде:
Вектор  называется пределом функции
называется пределом функции  при
при  , если для
, если для 
 такое, что для
такое, что для 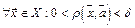 тотчас выполняется
тотчас выполняется 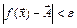 .
.
Пример 5.Доказать, что  .
.
Согласно определению оценим разность  . Получим, используя неравенство
. Получим, используя неравенство  для
для 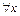 :
: 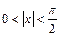 , что
, что  , откуда
, откуда  . Таким образом, для
. Таким образом, для 
 такое, что для
такое, что для  .
.
Отметим, что и в рассмотренном примере, и во многих других мы не решаем неравенство  , т.е. не находим множество тех и только тех значений
, т.е. не находим множество тех и только тех значений  , для которых оно имеет место. Наша цель – установить такую окрестность точки
, для которых оно имеет место. Наша цель – установить такую окрестность точки  , в которой неравенство заведомо выполняется.
, в которой неравенство заведомо выполняется.
Пример 6. Доказать, что  .
.
Оценим разность  . Имеем:
. Имеем:  . Множитель
. Множитель  не является ограниченным на множестве
не является ограниченным на множестве  , поэтому здесь необходимо выделить некоторую окрестность точки 2, в которой и проводить дальнейшие оценки, например, 1-окрестность, т.е. интервал (1,3). Для
, поэтому здесь необходимо выделить некоторую окрестность точки 2, в которой и проводить дальнейшие оценки, например, 1-окрестность, т.е. интервал (1,3). Для  имеем
имеем  , следовательно,
, следовательно,  . Так как
. Так как  - окрестность не должна выходить за пределы 1-окрестности, то положим
- окрестность не должна выходить за пределы 1-окрестности, то положим  , тогда из неравенства
, тогда из неравенства  будет следовать
будет следовать  .
.
Пример 7. Доказать, что  .
.
Требуется для  указать такое число
указать такое число  , что для любого
, что для любого  будет выполнено
будет выполнено  , следовательно
, следовательно  . В силу монотонности функции
. В силу монотонности функции  на интервале
на интервале  получим:
получим:  .
.
Итак, для 
 , что
, что  .
.
Пример 8. Доказать, что  .
.
Требуется для  указать
указать  такое, что при
такое, что при  .
.
Из последнего неравенства находим:
 , откуда получаем
, откуда получаем  .
.
Запишем на языке «  » утверждение «вектор
» утверждение «вектор  не является пределом функции
не является пределом функции  при
при  »:
»:
 такое, что
такое, что 

 , но
, но  .
.
Пример 9. Покажем, что  .
.
Рассмотрим разность

Используя неравенство  , получим:
, получим:

как только  для любого
для любого  .
.
Итак,  , что при
, что при 
 , но при этом
, но при этом  .
.
Пример 10.Доказать, что не существует  .
.
Пусть  - произвольное вещественное число.
- произвольное вещественное число.
 , если
, если  .
.
Тогда, для 
 ,
, 


(за счёт выбора соответствующего целого числа  ), но тем не менее
), но тем не менее  . Следовательно, для
. Следовательно, для 
 .
.
Пусть теперь  .
.
 , если
, если  ,
,  В этом случае,
В этом случае,  ,
, 
 ,
,  и
и  , что
, что  . Итак,
. Итак,  .
.
Доказаны важные теоремы:
1. Определения Гейне и Коши эквивалентны.
2. Если существует предел  , то этот предел единственный.
, то этот предел единственный.
Отметим важный факт: в определениях предела по Гейне и Коши не требуется, чтобы функция  была бы определена в точке
была бы определена в точке  , поэтому ни значение
, поэтому ни значение  , если
, если  , ни неопределённость
, ни неопределённость  не влияют на существование и величину
не влияют на существование и величину  .
.
Для числовой функции числового аргумента и векторной функции числового аргумента введём понятие одностороннего предела функции в данной точке  .
.
Определение Гейне:
Пусть  и
и  - предельная точка множества
- предельная точка множества  . Вектор
. Вектор  называется пределом функции
называется пределом функции  при
при  справа (слева), если для любой последовательности
справа (слева), если для любой последовательности  ,
, 
 ,
,  соответствующая последовательность значений функции
соответствующая последовательность значений функции  всякий раз сходится к
всякий раз сходится к  .
.
Определение Коши:
Пусть  и
и  - предельная точка множества
- предельная точка множества  . Вектор
. Вектор  называется пределом функции
называется пределом функции  при
при  справа (слева), если для
справа (слева), если для 
 такое, что для
такое, что для 
 справедливо неравенство
справедливо неравенство  .
.
Для обозначения левого и правого пределов используют следующую символику:
 ,
,  , если
, если  , и
, и  ,
,  , если
, если  .
.
Теорема:
Функция  имеет предел в точке
имеет предел в точке  тогда, и только тогда, когда существуют предел слева и предел справа и они равны:
тогда, и только тогда, когда существуют предел слева и предел справа и они равны:  .
.
Пример 11. Доказать, что 
 , если
, если  .
.
При  неравенство
неравенство  справедливо для любого
справедливо для любого  , если
, если  , поэтому для
, поэтому для  в качестве
в качестве  подойдёт любое положительное число. Если же
подойдёт любое положительное число. Если же 
 , то логарифмируя неравенство, получим:
, то логарифмируя неравенство, получим:  , откуда
, откуда  . Таким образом, для
. Таким образом, для 
 такое, что для
такое, что для  имеет место:
имеет место:  , т.е.
, т.е.  .
.
Рассмотрим неравенство:  . Логарифмируя, имеем:
. Логарифмируя, имеем:  , откуда
, откуда  . Следовательно, для
. Следовательно, для  ,
, 
 такое, что для любого
такое, что для любого  :
:  тотчас выполняется:
тотчас выполняется:  , т.е.
, т.е.  .
.
Приведённые выше примеры показывают, что, пользуясь только определением предела, мы можем лишь проверить, является ли данное число пределом данной функции или нет, но не имеем конструктивного метода вычисления предела.