Занятие 1. Волновые свойства частиц. Соотношение неопределенностей.

Краткие теоретические сведения

Основные формулы

Формула де Бройля, выражающая связь длины волны с импульсом движущейся частицы, для двух случаев:

а) в классическом приближении ( ):

б) в релятивистском случае (скорость частицы сравнима со скоростью света в вакууме; ):

Связь длины волны де Бройля с кинетической энергией частицы:

а) в классическом приближении:

б) в релятивистском случае:

где энергия покоя частицы (

Фазовая скорость волн де Бройля:

где круговая частота; волновое число ( ).

Групповая скорость волн де Бройля:

Соотношения де Бройля:

где энергия движущейся частицы; импульс частицы;

волновой вектор; ;

постоянная Планка ( ).

Соотношения неопределенностей:

а) для координаты и импульса частицы:

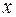где неопределенность проекции импульса частицы на ось ; неопределенность ее координаты;

б) для энергии и времени:

где неопределенность энергии данного квантового состояния; время пребывания системы в этом состоянии.

Вопросы для ответа у доски:

1. В чем заключается корпускулярно-волновой дуализм материи?

2. Укажите волновые и корпускулярные характеристики света.

3. Запишите формулу связи между ними.

4. Изложите идею де Бройля о дуализме по отношению к движущимся частицам.

5. Приведите известные вам опыты по экспериментальному доказательству волновых свойств микрочастиц.

6. Запишите соотношение неопределенностей для координаты и импульса.

7. Дайте иллюстрацию этого соотношения на примере прохождения электронов через узкую щель.

8. Запишите и объясните соотношение неопределенностей для энергии и времени.

9. В чем, опираясь на соотношение неопределенностей, состоит отличие описания поведения частиц в классической и квантовой теориях?