Возрастание и убывание функции.
Исследование функции, построение графика.
Учебно-практическое пособие
Возрастание и убывание функции.
Функция 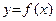 называется монотонно возрастающей в интервале хÎ(а, b), если для любых двух точек х1 и х2 этого интервала из неравенства х2 > х1 следует неравенство
называется монотонно возрастающей в интервале хÎ(а, b), если для любых двух точек х1 и х2 этого интервала из неравенства х2 > х1 следует неравенство 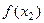 >
> 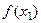 , то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
, то есть если любому большему значению аргумента из этого интервала соответствует большее значение функции.
Функция 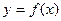 называется монотонно убывающей на интервале хÎ(а, b), если для любых двух точек х1 и х2 этого интервала из неравенства х2 > х1 следует неравенство
называется монотонно убывающей на интервале хÎ(а, b), если для любых двух точек х1 и х2 этого интервала из неравенства х2 > х1 следует неравенство 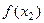 <
< 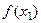 , то есть если любому большему значению аргумента из этого интервала соответствует меньшее значение функции.
, то есть если любому большему значению аргумента из этого интервала соответствует меньшее значение функции.
В области существования функции f(x) можно указать (в простейших случаях) конечное число интервалов возрастания и интервалов убывания функции, то есть интервалов монотонности функции.
Достаточный признак монотонности дифференцируемой функции:
если на интервале хÎ(а, b) производная 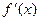 сохраняет знак, то функция
сохраняет знак, то функция 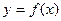 сохраняет монотонность на этом интервале, а именно:
сохраняет монотонность на этом интервале, а именно:
если  , то
, то 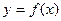 монотонно возрастает;
монотонно возрастает;
если 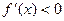 , то
, то 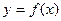 монотонно убывает.
монотонно убывает.
Пример 1.
Определить интервалы возрастания и убывания функции 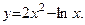
Решение.
Область определения данной функции: хÎ(0;+¥).
Интервалы возрастания найдем из достаточного признака возрастания: 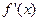 >0.
>0.
Так как 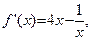 где
где 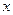 >0, то решаем систему неравенств:
>0, то решаем систему неравенств:
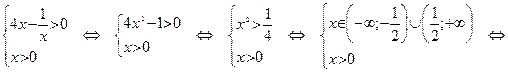
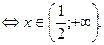
По достаточному признаку монотонности заключаем, что 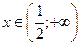 – это интервал возрастания данной функции (обозначается “”).
– это интервал возрастания данной функции (обозначается “”).
Интервалы убывания находим аналогично из достаточного признака убывания: 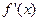 <0, то есть, решая систему неравенств:
<0, то есть, решая систему неравенств:
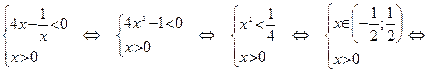
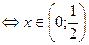 .
.
По достаточному признаку монотонности заключаем, что 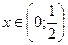 – это интервал убывания данной функции (обозначается “¯”).
– это интервал убывания данной функции (обозначается “¯”).
Ответ: функция 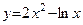 Š при
Š при 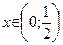 , ‰ при
, ‰ при 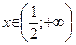 .
.
Пример 2.
Определить интервалы монотонности функции 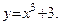
Решение.
Область определения функции: хÎ(-¥;+¥).
Находим производную 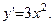 здесь
здесь 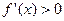 во всех точках, кроме
во всех точках, кроме 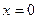 , где
, где 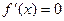 .
.
Следовательно, согласно достаточному признаку монотонности, данная функция 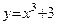 возрастает при всех х ¹ 0.
возрастает при всех х ¹ 0.
Далее очевидно, что для любого х1 > 0 будет 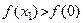 , а для любого х2 < 0 будет
, а для любого х2 < 0 будет  . Поэтому, согласно определению, функция
. Поэтому, согласно определению, функция 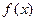 возрастает в любом интервале, включающем точку х = 0.
возрастает в любом интервале, включающем точку х = 0.
Ответ: при хÎ(-¥;+¥) функция 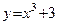 монотонно возрастает.
монотонно возрастает.
Пример 3.
Исследовать на возрастание и убывание функцию 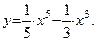
Решение.
Здесь 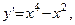 хÎ(-¥;+¥).
хÎ(-¥;+¥).
Решив уравнение х4 – х2 = 0, найдем точки х1 = 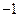 , х2 = 0, х3 = 1, в которых производная
, х2 = 0, х3 = 1, в которых производная 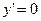 .
.
Так как 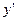 может изменять знак только при переходе через точки, в которых она обращается в нуль или терпит разрыв для непрерывности (в данном случае точки разрыва для
может изменять знак только при переходе через точки, в которых она обращается в нуль или терпит разрыв для непрерывности (в данном случае точки разрыва для 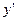 отсутствуют), то в каждом из интервалов (–¥;–1), (–1;0), (0;1), (1;+¥) производная сохраняет знак, поэтому в каждом из этих интервалов исследуемая функция монотонна. Чтобы выяснить, в каких из указанных интервалов функция возрастает, а в каких убывает, нужно определить знак производной в каждом из этих интервалов. Для этого достаточно просчитать знак
отсутствуют), то в каждом из интервалов (–¥;–1), (–1;0), (0;1), (1;+¥) производная сохраняет знак, поэтому в каждом из этих интервалов исследуемая функция монотонна. Чтобы выяснить, в каких из указанных интервалов функция возрастает, а в каких убывает, нужно определить знак производной в каждом из этих интервалов. Для этого достаточно просчитать знак 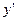 в какой-нибудь одной точке каждого интервала и результаты оформить в виде следующей схемы:
в какой-нибудь одной точке каждого интервала и результаты оформить в виде следующей схемы:
 |
Ответ: функция
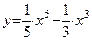 возрастает в интервалах (–¥;–1) и (1;+¥), убывает в интервале хÎ(–1;1).
возрастает в интервалах (–¥;–1) и (1;+¥), убывает в интервале хÎ(–1;1).
Задачи для самостоятельного решения.
Найти интервалы монотонности следующих функций:
1. 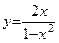 ; ;
| 4. 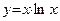
|
2. 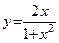
| 5. 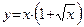 ; ;
|
3. 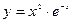 ; ;
| 6. 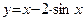
|
Ответы.
1. При 
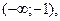 (–1;1) и (1;+¥) возрастает.
(–1;1) и (1;+¥) возрастает.
2. При 
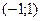 – возрастает; при
– возрастает; при 
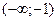 и (1;+¥) – убывает.
и (1;+¥) – убывает.
3. При  (0;2) – возрастает; при
(0;2) – возрастает; при 
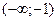 и (2;+¥) – убывает.
и (2;+¥) – убывает.
4. При 
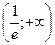 – возрастает; при
– возрастает; при 
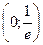 – убывает.
– убывает.
5. При  [0;+¥) – возрастает.
[0;+¥) – возрастает.
6. При 
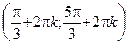 – возрастает;
– возрастает; 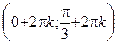 и
и 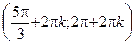 – убывает, где
– убывает, где 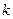 = 0, ±1, ±2,¼
= 0, ±1, ±2,¼