Кратчайший путь
Одна из самых известных задач, связанных с графами, — определение длины кратчайшего пути из одной вершины в другую.
Рассмотрим задачу № 3 из демонстрационного варианта ГИА
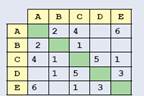
Между населенными пунктами A, B, C, D, Eпостроены дороги, протяженность которых приведена в таблице. Определите кратчайший путь между пунктами Aи D(при условии, что передвигаться можно только по построенным дорогам).
Уточним, что на самом деле в задаче требуется определить не сам кратчайший путь (последовательность ребер), а его длину. В условии дано еще 4 варианта ответа, но в данном случае они только мешают, поэтому мы их не приводим. Хотя задача сформулирована как практическая, она сводится к поиску кратчайшего пути в графе.
 Способ 1.Построение графа.
Способ 1.Построение графа.
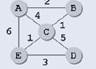
По заданной таблице (весовой матрице графа) определяем, что граф содержит 7 ребер: AB(длиной 2), AC(4), AE(6), BC(1), CD(5), CE(1) и DE(3).
Нарисуем граф, соответствующий этим данным (вершины можно располагать как угодно):
Теперь перебираем все возможные пути из вершины Aв вершину D, не проходящие дважды через одну и ту же вершину, и считаем их длины:
ABCD: 2 + 1 + 5 = 8
ABCED: 2 + 1 + 1 + 3 = 7
ACD: 4 + 5 = 9
ACED: 4 + 1 + 3 = 8
AECD: 6 + 1 + 5 = 12
AED: 6 + 3 = 9
Чтобы не запутаться и не потерять какой-то путь, мы сначала рассмотрели все пути, начинающиеся с ребра AB, затем — все пути, начинающиеся с ребра AC, и т.д. Более того, пути перебираются в так называемом лексикографическом порядке, то есть в таком порядке, в каком они были бы расположены в словаре (в данном случае — в английском). Такой порядок делает перебор систематическим и поэтому уменьшает вероятность пропуска какого-то пути.
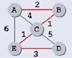 Сравнивая полученные длины, находим, что кратчайший путь ABCED(он выделен красным цветом) имеет длину 7:
Сравнивая полученные длины, находим, что кратчайший путь ABCED(он выделен красным цветом) имеет длину 7:
Прелесть этого способа состоит в том, что в простых задачах можно сразу увидеть ответ, перебрав все варианты в уме и таким образом сэкономив время. Однако при этом есть риск пропустить какой-то вариант (на это и рассчитаны отвлекающие варианты ответов — дистракторы).
 Способ 2.Построение дерева возможных путей.
Способ 2.Построение дерева возможных путей.
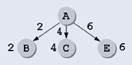
Можно использовать другой способ, при котором явно строится схема возможных путей в графе (структура типа “дерево”). Сначала по таблице определяем, что из исходной вершины Aможно ехать только в B, Cи E:
Числа около стрелок обозначают длины дорог (веса соответствующих ребер), а числа около вершин — расстояния от начальной вершины Aпо этому пути.
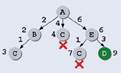 Далее рассматриваем все пути, состоящие из двух ребер: из Bможно ехать в C(или вернуться в A, но такой вариант нас не интересует), из C— в B, Dи Е, а из E— в Си D. Однако первый же из рассмотренных путей, ABC, имеет длину 3, что меньше, чем длина ребра AC(4). Поэтому все пути, начинающиеся с ребра AC, можно далее вообще не рассматривать — в любом случае переезд из Ав Cчерез Bбудет на 1 короче, чем напрямую. По этой же причине не нужно рассматривать пути, начинающиеся с AEC(длина этого пути равна 7, что больше уже известного пути в Cдлиной 3):
Далее рассматриваем все пути, состоящие из двух ребер: из Bможно ехать в C(или вернуться в A, но такой вариант нас не интересует), из C— в B, Dи Е, а из E— в Си D. Однако первый же из рассмотренных путей, ABC, имеет длину 3, что меньше, чем длина ребра AC(4). Поэтому все пути, начинающиеся с ребра AC, можно далее вообще не рассматривать — в любом случае переезд из Ав Cчерез Bбудет на 1 короче, чем напрямую. По этой же причине не нужно рассматривать пути, начинающиеся с AEC(длина этого пути равна 7, что больше уже известного пути в Cдлиной 3):
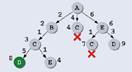 Итак, мы нашли один путь (AED) из Aв D, который имеет длину 9. Пока запоминаем его, однако нужно рассмотреть еще ветку ABC, которая может дать более короткий путь.
Итак, мы нашли один путь (AED) из Aв D, который имеет длину 9. Пока запоминаем его, однако нужно рассмотреть еще ветку ABC, которая может дать более короткий путь.
По таблице находим, что из Cможно ехать в B, Dи E. Возвращаться в Bнет смысла, поэтому рассматриваем последние два варианта:
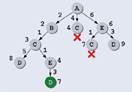 Получаем еще один (лучший на данный момент!) путь ABCDиз Aв Dдлиной 8. С другой стороны, длина пути ABCEменьше, чем длина предыдущего известного пути из Aв E(путь AE, длина 6), поэтому на этой ветке, возможно, удастся еще улучшить результат. И действительно, из Eимеет смысл ехать только в D(возвращаться в Aили в Cне стоит), и этот путь имеет длину 7:
Получаем еще один (лучший на данный момент!) путь ABCDиз Aв Dдлиной 8. С другой стороны, длина пути ABCEменьше, чем длина предыдущего известного пути из Aв E(путь AE, длина 6), поэтому на этой ветке, возможно, удастся еще улучшить результат. И действительно, из Eимеет смысл ехать только в D(возвращаться в Aили в Cне стоит), и этот путь имеет длину 7:
Таким образом, мы построили дерево, которое учитывает все возможные пути. Некоторые ветки дерева (ACи AEC) отсечены, потому что эти пути заведомо не улучшают результат. Длина кратчайшего пути ABCEDравна 7.
Способ 3.Перебор возможных путей без построения
дерева.
Сначала выпишем все ребра, соединяющие начальную вершину Aс другими вершинами, и их длины:
AB: 2
AC: 4
AE: 6
Теперь рассмотрим все пути, состоящие из двух ребер. Получив путь ABCдлиной 3, сразу отбрасываем все пути, проходящие через ребро AC(так же, как в способе 2):
ABC: 2 + 1 = 3
AEC: 6 + 1 = 7
AED: 6 + 3 = 9 (цель достигнута)
Видим, что все пути, проходящие через AEC, тоже можно отбросить. Остается проверить ветку ABC:
ABCD: 3 + 5 = 8 (цель достигнута)
ABCE: 3 + 1 = 4
Продолжая последнюю оставшуюся ветку ABCE, находим:
ABCED: 4 + 3 = 7 (цель достигнута)
Нерассмотренных путей, которые могли бы улучшить решение, больше не осталось, поэтому выбираем лучший путь: ABCEDдлиной 7.
Задачи для тренировки
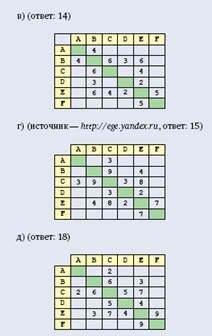 Между населенными пунктами A, B, C, D, E, Fпостроены дороги, протяженность которых приведена в таблице. Отсутствие числа в ячейке таблицы означает, что прямой дороги между пунктами нет.
Между населенными пунктами A, B, C, D, E, Fпостроены дороги, протяженность которых приведена в таблице. Отсутствие числа в ячейке таблицы означает, что прямой дороги между пунктами нет.
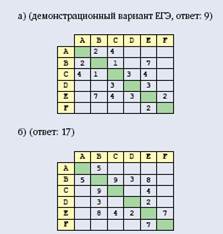 Определите длину кратчайшего пути между пунктами Aи F(при условии, что передвигаться можно только по построенным дорогам).
Определите длину кратчайшего пути между пунктами Aи F(при условии, что передвигаться можно только по построенным дорогам).