ВОПРОСЫ И УПРАЖНЕНИЯ

1.Сформулируйте и напишите математическое выражение закона всемирного тяготения. Каков физический смысл и числовое значение гравитационной постоянной в СИ, в каких единицах она измеряется?

2.Как рассчитывается сила гравитационного взаимодействия двух протяженных тел ?

3.Напишите выражение для потенциальной энергии материальной точки массой m, находящейся на расстоянии r от точечного источника гравитационного поля массой М. Изобразите графически зависимость этой энергии от расстояния r между этими точками.

4.Что называется: а) напряженностью; б) потенциалом гравитационного поля? Какова их взаимосвязь? В каких единицах измеряются напряженность и потенциал поля?

5.Как зависит ускорение свободного падения тел относительно поверхности Земли от: а) географической широты местности; б) высоты над уровнем моря?

6.Какая скорость тел относительно планеты или звезды называется: а) первой; б) второй космической? Как рассчитываются эти скорости?

7.Какие системы отсчета называются неинерциальными? Приведите примеры движений тел, для объяснения которых в системах отсчета, жестко связанных с Землей, необходимо учитывать неинерциальность этой системы отсчета.

8.Как описываются движения тел относительно прямолинейно и ускоренно движущейся системы отсчета? Напишите и объясните выражение для силы инерции в этом случае.

9.Рассмотрите поведение тел во вращающейся с постоянной угловой скоростью системе отсчета. Чему равна центробежная сила инерции?

10.В каком случае во вращающейся системе отсчета на тело действует сила Кориолиса? Каково направление и чему равен модуль этой силы?

11.Напишите и объясните основное уравнение динамики для материальной точки массой m в неинерциальной системе отсчета, вращающейся с постоянной угловой скоростью 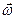вокруг оси, которая перемещается поступательно с ускорением а0 относительно какой-нибудь инерциальной системы отсчета.

12.Каковы особенности сил инерции, отличающие их от сил взаимодействия тел? Как Вы понимаете принцип эквивалентности сил инерции и сил поля тяготения?

ЗАДАЧИ

5.1.Определить массу М и среднюю плотность ρ Земли по следующим данным: средний радиус Земли R = 6,37·10⁶ м, ускорение свободного падения на поверхности Земли g = 9,81 м/с², гравитационная постоянная γ = 6,67·10^-11 м³/(кг·с²).

5.2.Определить массу М Земли по следующим данным:, гравитационная постоянная γ = 6,67·10^-11 м³/(кг·с²), период обращения Луны вокруг Земли Т = 2,36·10⁶ с, среднее расстояние между центрами Земли и Луны γ = 3,84·10⁸ м.

5.3.Ближайший спутник Марса находится на расстоянии r = 9,4·10⁶ м от центра планеты и движется вокруг нее со скоростью v = 2,1·10³ м/с. Зная, что гравитационная постоянная γ = 6,67·10^-11 м³/(кг·с²), определить массу М Марса.

5.4.Вычислить массу М Солнца по следующим данным; гравитационная постоянная γ = 6,67·10^-11 м³/(кг·с²), расстояние от Земли до центра Солнца r = 1,5·10¹¹ м, период обращения Земли вокруг Солнца Т = 3,16·10⁷ с.

5.5.Определить силу F гравитационного взаимодействия материальной точки массой m и тонкого однородного стержня массой М, длина которого l, если они расположены на одной прямой на расстоянии а друг от друга.

5.6.Тонкое однородное полукольцо массой М и радиусом R взаимодействует с однородным шариком массой т, помещенным в центре кривизны. Найти силу F гравитационного взаимодействия этих тел.

5.7.Найти силу F, с которой кольцо из однородной, тонкой проволоки радиусом r, притягивает однородный шарик массой т, находящийся на оси кольца на расстоянии h от его центра. Плотность материала проволоки ρ. Радиус кольца R.

5.8.Тонкий однородный диск радиусом R имеет массу М. Найти силу гравитационного взаимодействия этого диска и частицы массой т, находящейся на оси диска на расстоянии h от его центра.

5.9.Определить модуль F гравитационной силы, с которой очень тонкий однородный слой в виде полусферы радиусом R и массой М действует на частицу массы m, находящуюся в ее центре.

5.10.Определить гравитационную силу F, действующую на материальную точку, находящуюся внутри однородного сферического слоя вещества.

5.11.Найти зависимость периода T обращения искусственного спутника, вращающегося по круговой орбите вблизи поверхности сферического тела, от средней плотности ρ его вещества.

5.12.Луна движется вокруг Земли со скоростью v = 1,02·10³ м/с. Среднее расстояние до Луны от центра Земли 60,3 радиуса Земли. Найти скорость u, с которой должен обращаться искусственный спутник Земли на небольшой высоте над ее поверхностью.

5.13.Некоторая планета движется по окружности вокруг Солнца со скоростью v. Определить: а) период T обращения этой планеты; б) радиус r ее орбиты. Массу Солнца М и гравитационную постоянную считать известными.

5.14.Период обращения Урана вокруг Солнца в 84 раза больше периода обращения Земли. Считая орбиты планет круговыми, найти; а) во сколько раз п расстояние от Урана до Солнца превышает расстояние от Земли до Солнца; б) скорость v и ускорение а Урана в гелиоцентрической системе отсчета. Расстояние от Земли до Солнца r = 1,5·10¹¹ м, период обращения Земли вокруг Солнца Т = 3,16·10⁷ с.

5.15.Планета Нептун находится в 30 раз дальше от центра Солнца, чем Земля. Определить период Т обращения Нептуна вокруг Солнца.

5.16.Некоторая планета движется вокруг Солнца по эллипсу так, что минимальное расстояние между ней и Солнцем равно r, а максимальное – R. Найти с помощью законов Кеплера период Т обращения ее вокруг Солнца. Массу Солнца M и гравитационную постоянную γ считать известными.

5.17.Планета массой т движется по эллипсу вокруг Солнца так, что наибольшее и наименьшее расстояния ее от Солнца равны соответственно r1 и r2 . Найти момент импульса L планеты относительно центра Солнца. Массу М Солнца и гравитационную постоянную γ считать известными.

5.18.Небольшое тело начинает падать на Солнце с расстояния, равного радиусу земной орбиты. Начальная скорость тела в гелиоцентрической системе отсчета равна нулю. Найти с помощью законов Кеплера, сколько будет продолжаться падение. Период обращения Земли вокруг Солнца Т = 365,25 сут.

5.19.В однородном шаре плотностью ρ и радиусом R проделано вдоль оси узкое цилиндрическое отверстие. Определить работу A, совершаемую против гравитационной силы при перемещении частицы массой m из центра шара на его поверхность.

5.20.Найти работу А, совершаемую против гравитационной силы при перемещении частицы массой m от поверхности шара в бесконечность. Радиус шара R и его плотность ρ.

5.21.На каком расстоянии r от центра Луны находится точка, в которой напряженность результирующего поля тяготения Земли и Луны равна нулю? Считать, что масса Земли в 81 раз больше массы Луны, а расстояние между центрами Луны и Земли в 60 раз больше радиуса Земли. Радиус Земли Rз = 6,37·10⁶ м.

5.22.Однородный шар имеет массу М и радиус R. Найти давление р внутри шара, обусловленное гравитационным сжатием, в зависимости от расстояния r до его центра.

5.23.Частица, масса которой т, находится внутри однородного шара массой М и радиусом R на расстоянии r от его центра. Найти гравитационную силу F, действующую на частицу.

5.24.Телу сообщили на полюсе Земли скорость v0, направленную вертикально вверх. Зная радиус Земли R и ускорение свободного падения g на ее поверхности, найти высоту h, на которую поднимается тело. Сопротивление воздуха не учитывать.

5.25.Искусственный спутник выведен на круговую орбиту вокруг Земли со скоростью v относительно поступательно движущейся системы отсчета, связанной с осью вращения Земли. Найти расстояние h от поверхности Земли до спутника. Радиус Земли R и ускорение свободного падения на поверхности Земли g считать известными.

5.26.Искусственный спутник Земли движется по эллиптической орбите, эксцентриситет которой е = 0,50. Во сколько раз и линейная скорость спутника в перигее больше, чем в апогее?

5.27.Для осуществления всемирной телевизионной связи достаточно иметь три спутника Земли, вращающихся по круговой орбите в плоскости экватора с запада на восток и расположенных друг относительно друга под углом φ = 120°. Периоды обращения этих спутников должны быть равны периоду обращения Земли вокруг собственной оси. Зная, что гравитационная постоянная γ = 6,67·10^-11 м³/(кг·с²) и масса Земли М = 5,96·10²⁴ кг, определить радиус орбиты r и линейную скорость v таких спутников.

5.28.Спутник должен двигаться в экваториальной плоскости Земли вблизи ее поверхности. Во сколько раз n энергия, необходимая для запуска спутника в направлении вращения Земли, меньше энергии, необходимой для запуска в противоположном направлении? Сопротивление воздуха не учитывать. Радиус Земли R = 6,37·10⁶ м, период обращения Земли вокруг собственной оси Т = 8,64·10⁴ с.

5.29.Определить минимальную работу А, которую необходимо совершить, чтобы тело массой m удалить с поверхности Земли в бесконечность, если работа сил сопротивления составляет n-ю часть искомой работы. Массу Земли М, ее радиус R и гравитационную постоянную γ считать известными.

5.30.Найти наименьшую скорость v, которую необходимо сообщить телу относительно поверхности Земли на экваторе, чтобы оно смогло покинуть Солнечную систему. Сопротивление воздуха не учитывать. Считать известными: гравитационную постоянную γ = 6,67·10^-11 м³/(кг·с²), массу Солнца MC = 1,97·10³⁰ кг, массу Земли МЗ = 5,96·10²⁴ кг, расстояние от центра Солнца до Земли r = 1,5·10¹¹ м, радиус Земли R3 = 6,37·10⁶ м, период обращения Земли вокруг собственной оси Т = 8,64 ·10⁴ с.

5.31.Кабина корабля движется поступательно относительно инерциальной системы отсчета с постоянным ускорением a0. Определить силу инерции F, действующую на тело массой т. Зависит ли эта сила от; а) положения; б) скорости тела относительно кабины?

5.32.Вагон, к потолку которого на нерастяжимой нити подвешен шарик массой т, начинает двигаться по прямолинейному горизонтальному пути с ускорением a0. Найти: а) силу инерции Fин, действующую на шарик, в вагоне; б) в каком направлении и на какой угол α0 от вертикали отклонится нить?

5.33.Кабина лифта движется по вертикали вниз с ускорением а0. Определить силу инерции Fин, действующую в кабине на тело массой т. При каком ускорении а01 кабины лифта все тела в ней будут находиться в состоянии невесомости?

5.34.
Брусок массой т, находящийся на наклонной плоскости, удерживается на ней силой трения. Определить время t, за которое брусок спустится по наклонной плоскости на расстояние l = 0,98 м, если она станет двигаться с ускорением a0 = 0,98 м/с в горизонтальном направлении (рис. 5.1).Угол наклона плоскости к горизонту α = 30°. Коэффициент трения между бруском и плоскостью μ = 0,6. При решении задачи воспользоваться системой отсчета, связанной с наклонной плоскостью.

5.35.На горизонтальном прямолинейном участке пути железнодорожный вагон тормозится и его скорость равномерно изменяется от v1 = 54 км/ч до v2 = 36 км/ч за время t = 2,5 с. Определить силу инерции Fин действующую на чемодан массой т = 18 кг, лежащий на горизонтальной полке вагона. При каком минимальном значении коэффициента трения μmin между чемоданом и полкой чемодан начнет скользить по полке?

5.36.Горизонтально расположенная платформа вращается с угловой скоростью 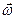вокруг вертикальной оси, проходящей через ее центр. Найти центробежную силу инерции Fцб, действующую на тело массой т, находящееся на расстоянии r от оси вращения.

5.37.Платформа (см. условие задачи 5.36) вращается с угловой скоростью ω = 7,33 рад/с. На каком максимальном удалении rmax от оси вращения нужно поместить тело, чтобы оно не соскальзывало? Коэффициент трения тела о платформу μ = 0,44.

5.38.На внутренней поверхности конуса с углом при вершине 2а (рис. 5.2) на высоте h от вершины находится небольшое тело. Коэффициент трения между телом и поверхностью конуса равен μ. Найти минимальную угловую скорость ωmin вращения конуса вокруг вертикальной оси, при которой тело будет неподвижно относительно конуса.

5.39.В аттракционе "мотоциклетные гонки на вертикальной стене" .трек представляет собой вертикальную цилиндрическую поверхность диаметром d = 18 м. С какой скоростью v должен двигаться мотоциклист, чтобы не соскальзывать с трека? Коэффициент трения μ = 0,80.

5.40.При какой угловой скорости ω вращения звезды с ее экватора начнет истекать вещество? Для решения использовать систему отсчета, связанную с вращающейся звездой. Масса звезды равна М, а ее радиус R.

5.41.Тело массой т находится на экваторе. Определить, на сколько ΔF изменится сила, действующая на поверхность Земли, если тело, движущееся с востока на запад с постоянной скоростью v, изменит направление на противоположное.

5.42.Горизонтальный диск вращают с постоянной угловой скоростью ω = 9,0 рад/с вокруг вертикальной оси, проходящей через его центр. Вдоль одного из диаметров диска движется небольшое тело массой т = 0,6 кг с постоянной относительно диска скоростью ω = 0,9 м/с. Найти силу F, с которой диск действует на это тело в момент, когда оно находится на расстоянии р = 0,50 м от оси вращения.

5.43.Горизонтально расположенный диск вращается с постоянной угловой скоростью 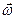вокруг вертикальной оси, проходящей через его центр. По диску движется равномерно на неизменном расстоянии от оси вращения частица. Определить мгновенные значения скорости v' относительно диска, при которых сила Кориолиса будет уравновешиваться центробежной силой инерции. Выразить v' через r - мгновенные значения радиуса-вектора, проведенного к частице от центра диска.

5.44.Горизонтально расположенный стержень вращается вокруг вертикальной оси, проходящей через его конец, с постоянной угловой скоростью ω = 2 рад/с. Расстояние от оси до другого конца стержня l = 1,2 м. На стержень надета небольшая муфта массой т = 0,2 кг. Муфта закреплена с помощью нити на расстоянии l0 = 0,2 м от оси вращения. В момент t = 0 нить пережигают, и муфта начинает скользить по стержню практически без трения. Найти: а) время t = τ, спустя которое муфта соскользнет со стержня; б) силу F, с которой стержень действует на муфту в момент τ = t; в) работу А по перемещению муфты за время т.

5.45.С вершины гладкой сферы радиусом R = 1 м начинает соскальзывать небольшое тело массой m = 0,30 кг. Сфера вращается с постоянной угловой скоростью ω = 6,0 рад/с вокруг вертикальной оси, проходящей через ее центр. Найти в системе отсчета, связанной со сферой, центробежную Fцб и кориолисову Fкор силы инерции в момент отрыва тела от поверхности сферы.

5.46.Определить поперечное смещение х пули, выпущенной в плоскости меридиана по горизонтальному направлению, за первую секунду ее полета. Выстрел произведен в северном полушарии Земли на широте φ = 60⁰, начальная скорость пули v = 10³ м/с. В какую сторону отклонится пуля, если в момент выстрела ствол ружья был направлен на север. Силу сопротивления воздуха не учитывать. Скорость v пули считать постоянной.

5.47.Поезд массой m = 2,5·10⁶ кг идет с юга на север со скоростью v = 72 км/ч по железнодорожному пути, проложенному по меридиану. Определить горизонтальную составляющую F силы давления поезда на рельсы на широте φ = 60⁰ в северном полушарии.

5.48.Поезд массой m = 2,5·10⁶ кг движется со скоростью v = 54 км/ч в северном полушарии на широте V = 60° по железнодорожному пути, проложенному по параллели. Определить горизонтальную составляющую F силы давления поезда на рельсы.

5.49.Небольшое тело падает без начальной скорости с высоты h = 37,1 м. В какую сторону и на какое расстояние х от вертикали отклонится тело за время падения. Сопротивление воздуха не учитывать. Найденное значение х сравнить с разностью Δs путей, которые за время падения тела проходит точка, находящаяся на высоте h, и точка, находящаяся на земной поверхности, вследствие вращения Земли.

5.50.Для создания искусственной силы тяжести на космическом корабле, вращающемся вокруг Земли по круговой орбите, было предложено ускорять корабль до скорости и превышающей первую космическую скорость. Чтобы удержать корабль на круговой орбите при такой скорости, включается двигатель, сообщающий кораблю ускорение, нормальное к траектории корабля. При какой скорости v космонавт на корабле будет испытывать такую же "тяжесть", как и на Земле. Считать, что орбита проходит вблизи поверхности Земли. Изменением ускорения свободного падения g с высотой пренебречь.

 

 

Задание 6. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ