ВОПРОСЫ И УПРАЖНЕНИЯ
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Ижевский государственный технический университет
имени М.Т. Калашникова»
(ФГБОУ ВПО «ИжГТУ имени М.Т.Калашникова»)
ГЛАЗОВСКИЙ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
(филиал) ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова»
Физика 1
Задания к практическим занятиям.
| |
| Утверждено на заседании кафедры «Специальные инженерные науки» ГИЭИ (филиала) ФГБОУ ВПО «ИжГТУ им. М. Т. Калашникова» от 26.08.2014, протокол № 4. |
«Физика 1». Задания к практическим занятиям. Для студентов, обучающихся по направлениям: 151900.62 – Конструкторско-технологическое обеспечение машиностроительных производств (профиль – технология машиностроения) и 230100.62 Информатика и вычислительная техника (профиль – автоматизированные системы обработки и управления) – Глазов: Глазовский инженерно-экономический институт, 2014. –с.56.
Составитель – А.Б. Федоров.
Рецензент – д-р физ.-мат. наук, проф. В.А. Саранин (ГОУ ВПО ГГПИ им. В.Г. Короленко).
Настоящее пособие написано в соответствии с программой курса физики для специальностей 151900.62 – Конструкторско-технологическое обеспечение машиностроительных производств (профиль – технология машиностроения) и 230100.62 Информатика и вычислительная техника (профиль – автоматизированные системы обработки и управления). Оно представляет собой систему заданий, включающих вопросы и упражнения по тематике практических занятий и задачи для индивидуального решения, а также содержит справочный материал. Задачи подобраны из различных учебных пособий (И. Е. Иродов. Задачи по общей физике; А.Г. Чертов, А.А. Воробьев. Задачник по физике; В.С. Волькенштейн. Сборник задач по общему курсу физики и др.).
© ГИЭИ (филиал) ФГБОУ ВПО
| |
СОДЕРЖАНИЕ
ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ И СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Задание 1. Кинематика……………………………………….…………………….………….……4
Задание 2. Динамика материальной точки…………………………………………………………9
Задание 3. Законы сохранения…………………………………..…………………………………15
Задание 4. Динамика твердого тела………………………….……………………………….……21
Задание 5. Гравитационное поле. Неинерциальные системы отсчета…..………………………28
Задание 6. Элементы специальной теории относительности….…………………………………33
Задание 7. Механические колебания и волны…………………..…………………………………37
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Задание 8. Молекулярно-кинетическая теория идеальных газов..………………………………41
Задание 9. Основы термодинамики………………………………..………………………………45
Задание 10. Реальные газы. Фазовые равновесия и переходы…..………………………………49
Приложения………………………….…………………………..……………………….…………53
Литература………………………………………………………..…………………………………56
ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
И СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Задание 1. КИНЕМАТИКА
ВОПРОСЫ И УПРАЖНЕНИЯ
1. Что изучает механика как один из разделов физики? Каково содержание: а) ньютоновской; б) релятивистской; в) квантовой механики?
2. Почему при изучении реальных физических явлений и объектов приходится использовать модельные представления и абстрагированные понятия? Дайте определение: а) материальной точки (частицы); б) системы материальных точек; в) абсолютно твердого тела.
3. Каково содержание понятий пространства и времени в классической механике? Что означают понятия "однородность и изотропность пространства'", "однородность времени"?
4. Какие существуют способы описания движения материальной точки? Что представляет собой система отсчета, система координат? Что называется радиусом-вектором 
?
5. Покажите, что задание кинематического закона движения в координатной форме х = х(t), y = y(t), z = z(t) эквивалентно заданию его в векторной форме 
, где х, у, z - декартовы координаты материальной точки, -ее радиус-вектор. Каковы преимущества векторного описания движения?
6. Дайте определение кинематических величин: а) перемещения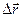 
; б) скорости 
; в) ускорения 
. В каких единицах измеряются эти величины? Как ориентированы векторы скорости и ускорения относительно траектории и друг друга?
7. Частица движется по закону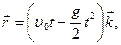 
где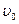 
и g - известные постоянные; 
k - орт координатной оси z. Найдите скорость v частицы и ее ускорение а, а также их проекци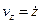и 
и 
как функции времени.
8. Ускорение движущейся частицы а = Аi, где А - известная постоянная; i - орт координатной оси х. В момент времени t = 0 х = x0 и vx = v0, где х0 и v0 – известные постоянные (начальные условия). Найдите проекцию скорости vх = х и координату х как функции времени.
9. Какое движение абсолютно твердого тела называется: а) поступательным; б) вращательным? Приведите примеры таких движений.
10. Что называется тангенциальным аτ и нормальным аn; ускорениями? Чему они равны? От чего зависит угол между векторами скорости v и полного ускорения а движущейся материальной точки?
11. Какие векторы называют аксиальными? Дайте определение:а) угла поворота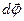 
твердого тела: б) угловой скорости 
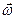; в) углового ускорения 
относительно неподвижной оси вращения. В каких единицах измеряются эти величины?
12. Колесо вращается вокруг неподвижной оси, проходящей через его центр масс. Обладает ли любая точка на ободе тангенциальным и нормальным ускорениями, если вращение происходит: а) с постоянной угловой скоростью; б) с постоянным угловым ускорением? Изменяются ли при этом модули этих ускорений?
ЗАДАЧИ
1.1. При движении велосипедиста и пешехода в одну сторону за каждые Δt1 = 1 мин пешеход отстает от велосипедиста на l1 = 210 м, а если, не изменяя по модулю скорости, они движутся навстречу друг другу, то за каждые Δt2 = 2 мин расстояние между ними уменьшается на l2 = 780 м. Найти скорость v1 велосипедиста и v2 пешехода.
1.2. Моторная лодка, двигаясь против течения реки, поравнялась с плотом в пункте А. Через τ = 30 мин после встречи лодка повернула обратно и нагнала плот в пункте В. Чему равно расстояние между пунктами A и В, если скорость течения реки u = 3,5 км/ч, а скорость лодки относительно воды постоянна?
| 
|
1.3. Два самолета одновременно вылетают из одного пункта по направлениям, составляющим угол α = 60°; один со скоростью v1 = 600 км/ч, другой – со скоростью v2 = 900 км/ч. Как возрастает со временем расстояние между самолетами? Чему равно это расстояние в тот момент, когда первый самолет пролетел путь s = 950 км? Найти скорость, с которой самолеты удаляются друг от друга.
1.4. Расстояние между двумя пунктами катер проходит по течению за время t1 = 5 ч, а против течения – за t2 = 12 ч. Найти расстояние между этими пунктами и скорость течения реки, если скорость катера относительно воды v' = 19 км/ч.
1.5. Лодка движется перпендикулярно к берегу реки со скоростью v' = 7,2 км/ч. Течение относит ее на расстояние L = 160 м вниз по реке. Ширина реки H = 400 м. Найти скорость течения реки и время, затраченное на переезд через реку.
1.6. Корабль идет на запад со скоростью и = 6,5 м/с. Известно, что ветер дует с юго-запада. Скорость ветра, зарегистрированная приборами относительно палубы корабля, v' = 9,3 м/с. Найти скорость ветра относительно земли. Какое направление ветра показывали приборы относительно курса корабля?
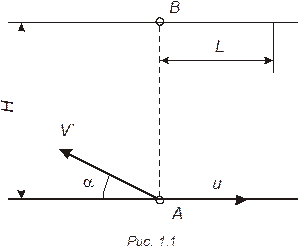
1.7. Лодочник, переправляясь из пункта А (рис. 1.1) через реку шириной H, направляет лодку под углом α к берегу. Найти скорость лодки относительно воды, если скорость течения реки u, а лодку отнесло ниже пункта В на расстояние L.
1.8. Из пункта А (рис. 1.2) одновременно вышли два катера, развивая относительно воды одинаковую скорость v'. Один пересек реку из пункта А в пункт В и обратно строго перпендикулярно к берегам, а второй проделал путь из пункта А в пункт С и обратно вдоль берега. Расстояния |АВ| = |АС| = l, скорость течения реки и. Какое время затратил каждый из катеров на свой путь?
1.9. Две частицы движутся с постоянными скоростями v1 и v2 по двум взаимно перпендикулярным прямым к точке их пересечения 0. В момент t = 0 частицы находились на расстояниях 11 и l2 от точки 0. Через какое время после этого расстояние между частицами станет наименьшим? Чему оно равно?
1.10. Из точек А и В (рис. 1.3), расстояние между которыми l0 = 10 м, начинают одновременно двигаться две материальные точки со скоростями v1 = 1,5 м/с и v2 = 4 м/с по направлениям, составляющим с линией АB углы α = 90° и β = 300 соответственно. Каким будет наименьшее расстояние между этими точками?
1.11. Уравнение движения материальной точки по прямой имеет вид 
где А = 2 м, В = 2 м/с, С = -0,5 м/с2. Найти момент времени, в который скорость точки v = 0. Чему равны координатах и ускорение точки в этот момент? Построить графики координаты, пути, скорости и ускорения этого движения в зависимости от времени.
1.12. Частица движется вдоль прямой по закону х = А + Bt + Ct3, где А = 3 м; В = 2,5 м/с, С = 0,25 м/с3. Найти средние значения скорости и ускорения за интервал времени от t1 = 1 с до t2 = 6 с. Построить графики зависимостей скорости и ускорения от времени.
1.13. Материальная точка движется в плоскости ху по закону х = At, у = B/t, где А и В – положительные постоянные. Найти скорость v и ускорение а в зависимости от времени. Как направлен вектор ускорения? Записать уравнение траектории у(х) , начертить ее график.
1.14. Прямолинейное движение материальной точки описывается законом х = 0,5t3 – 8t2. Найти экстремальное значение скорости v1 точки. Какому моменту времени t1 от начала движения оно соответствует? В какой момент времени t2 скорость точки v2 = 0?
1.15. Движение материальной точки в плоскости ху описывается уравнениями x = A cosωt, y = B sinωt, где A, В, ω – постоянные. Определить уравнение траектории у(х) движущейся точки; построить ее график.
1.16. Частица движется прямолинейно с ускорением а = 2В, где В = -0,5 м/с2. В момент t = 0 координата частицы x0 = 0, скорость v0 = At, где А = 2 м/с. Найти: а) скорость частицы в конце третьей секунды; б) модуль средней скорости за первые 3 с движения; в) путь, пройденный частицей за это время.
1.17. Скорость прямолинейно движущейся частицы изменяется по закону v = At - Bt2, где A и В – положительные постоянные. Найти: а) экстремальное значение скорости частицы; б) координату x частицы для этого же момента времени, если в момент t = 0 x0 = 0.
1.18. Частица движется прямолинейно с ускорением, изменяющимся во времени и по закону а = At2, где А = 0,3 м/с4 . Найти приращение скорости частицы за первые 4 с движения. Какой путь прошла частица за это время?
1.19. Компоненты ускорения частицы, движущейся в плоскости ху, равны: ах = 2А, аy = 2В, где А и В – положительные постоянные. В момент t = 0 координаты частицы x0 = у0 = 0, скорость v0 = 0. Найти: а) модули скорости и ускорения частицы в зависимости от времени; б) уравнение траектории y(x) частицы; построить ее график.
1.20. Материальная точка движется в плоскости ху так, что компоненты ее скорости равны: ax=A, vy = A(1 – 2Bt), где -A и В – положительные постоянные. Найти: а) модули скорости и ускорения точки в зависимости от времени; б) экстремальное значение координаты у1 и значение координаты х1, соответствующей этому же моменту времени, если в момент t = 0 координаты точки x0 = у0 = 0.
1.21. Радиус-вектор движущейся частицы определяется выражением r = 3t2i + 4t2j + 7k. Найти перемещение частицы Δr за первые 10 с движения и модуль этого перемещения |Δr |.
1.22. Начальная скорость частицы v1 = li + 3j + 5k, конечная v = 2i + 4j + 6k. Найти приращение скорости Δv, модуль приращения скорости |Δv| и приращение модуля скорости Δv.
1.23. Радиус-вектор материальной точки изменяется со временем по закону r = 3t2i + 2tj + 1k. Найти зависимости от времени векторов скорости и ускорения точки и модулей этих величин.
1.24. Две частицы в момент t = 0 одновременно начинают двигаться вдоль оси х таким образом, что их радиусы-векторы изменяются со временем по законам: r1 = 2t2i, r2 = (20 – 3t)i. Найти: а) радиус-вектор r0 точки встречи частиц; б) скорости v1 и v2 частиц в момент встречи.
1.25. Две частицы движутся с постоянными скоростями v1 и v2. Их радиусы-векторы в начальный момент времени равны r1 и r2.При каком соотношении между этими четырьмя векторами частицы столкнутся друг с другом?
1.26. Скорость материальной точки, движущейся в плоскости ху, изменяется со временем по закону v = Ai - 2Btj, где А и. В — положительные постоянные. Найти: а) зависимость от времени модуля скорости точки; б) ускорение а точки и его модуль; в) зависимость радиуса-вектора r точки от времени, если в момент t = 0 он был равен нулю.
1.27. Скорости двух частиц, движущихся вдоль оси х, изменяются со временем по законам: v1 = 4i, v2 = -0,8ti. В момент t= 0 их координаты x0 = 0, х2 = 15 м соответственно. Найти: а) радиус-вектор точки встречи частиц; б) модули скоростей v1 и v2 частиц в момент встречи τ.
1.28. Скорость частицы, движущейся вдоль оси x, изменяется со временем по закону v = (1 – 2Bt)i, где В - положительная постоянная, В момент t = 0 координата частицы х = 0. Найти промежуток времени, по истечении которого частица вернется в исходную точку, а также путь, который она пройдет за это время.
| 
|
1.29. Скорость частицы, движущейся в плоскости ху, изменяется со временем по закону v = (1 - 0,5t)I + 4j. В момент t = 0 координаты частицы х0 = у0 = 0. Найти экстремальное значение координаты x1 частицы и координату y1, соответствующую этому же моменту времени. Записать зависимость радиуса-вектора r частицы от времени.
1.30. Частица движется в плоскости ху со скоростью v = Ai + Bxj, где А и В – постоянные. В начальный момент времени координаты частицы х = у0 = 0. Найти зависимость от времени радиуса-вектора r частицы и уравнение траектории у(х).
1.31. По ледяной горке пустили скользить снизу вверх шайбу. На расстоянии l = 3 м от начальной точки шайба побывала дважды: через t1 = 2 с и t2 = 10 с после начала движения. Считая ускорение постоянным, найти его модуль и начальную скорость шайбы.
1.32. С вышки одновременно брошены два тела с одинаковой по модулю начальной скоростью v0; одно – вертикально вверх, другое – вертикально вниз. Как с течением времени будет изменяться расстояние между этими телами? Чему будет оно равно в момент t, когда первое тело достигнет наивысшей точки своего движения?
1.33. Частице А сообщили начальную скорость v0, направленную вертикально вверх. В тот же момент времени с высоты h начала падать без начальной скорости частица В. Пренебрегая сопротивлением воздуха, найти зависимость от времени расстояния между частицами. Чему равно это расстояние в момент τ, когда частица В упала на землю?
1.34. Ракета, запущенная вертикально вверх, в течение t1 = 10 с работы двигателя движется с ускорением а = 2g, Затем двигатель отключается. Найти максимальную высоту подъема ракеты и скорость падения ее на землю. Начертить график зависимости скорости от времени для всего полета. Торможением после отключения двигателя и сопротивлением воздуха пренебречь.
1.35. С высоты Н бросили камень в горизонтальном направлении со скоростью v0. Пренебрегая сопротивлением воздуха, найти: а) уравнение траектории у(х) движения камня; б) скорость падения камня на землю и угол, который она составит с горизонтом; в) расстояние, которое пролетит камень от места бросания по горизонтали.
1.36. Тело брошено горизонтально с начальной скоростью v0 = 10 м/с. Через τ = 2 с после начала движения, пренебрегая сопротивлением воздуха, найти: а) угол между вектором скорости и вертикалью; б) модули тангенциального и нормального ускорений; в) радиус кривизны траектории в точке, соответствующей этому моменту времени.
1.37. Из одной точки одновременно бросили два тела: одно — вертикально вверх, другое – горизонтально. Начальная скорость каждого тела v0 = 15 м/с. Пренебрегая сопротивлением воздуха, найти расстояние между телами через τ = 1,5 с.
1.38. Из трех труб, расположенных на земле, с одинаковой начальной скоростью бьют струи воды под углами α1 = 60°, α2 = 45°, α3 = 30° к горизонту. Пренебрегая сопротивлением воздуха, найти; а) отношение Н1: Н2: Н3 максимальных высот подъема этих струй; б) отношение L1: L2: L3 дальностей падения воды на землю.
1.39. Снаряд вылетает из орудия под углом α = 45° к горизонту с начальной скоростью v0 = 500 м/с. Через τ = 20 с после начала движения, пренебрегая сопротивлением воздуха, найти; а) модуль скорости снаряда; б) угол, который составляет вектор скорости v с осью х; в) модули нормального и тангенциального ускорений снаряда; г) радиус кривизны траектории в точке, соответствующей этому моменту времени.
1.40. С палубы корабля, идущего со скоростью и, выпущен вертикально вверх снаряд с начальной скоростью v0 относительно корабля. Пренебрегая сопротивлением воздуха, найти в неподвижной системе отсчета, связанной с водой: а) зависимость от времени модуля v; б) угол между вектором скорости снаряда и осью у в зависимости от времени; в) уравнение траектории снаряда у(х).
1.41. Небольшое тело начинает движение по окружности радиусом R = 30 м с постоянным по модулю тангенциальным ускорением аτ = 5 м/с2. Найти полное ускорение тела через τ = 3 с после начала движения.
1.42. Материальная точка движется по окружности радиусом R = 5 м. Когда нормальное ускорение точки становится ап = 3,2 м/с2, угол между векторами полного и нормального ускорений φ = 60°. Найти модули скорости и тангенциального ускорения точки для этого момента времени.
1.43. Нормальное ускорение частицы, движущейся по окружности радиусом R = 3,2 м, изменяется по закону ап = At2, где А = 2,5 м/с4. Найти: а) путь, пройденный частицей за τ = 5 с после начала движения; б) тангенциальное и полное ускорения в конце этого участка пути.
1.44. Автомобиль, движущийся со скоростью v = 54 км/ч, проходит закругление шоссе радиусом кривизны R = 375 м. На повороте шофер тормозит машину, сообщая ей ускорение аτ = 0,5 м/с2. Найти модули нормального и полного ускорений автомобиля на повороте и угол между их направлениями.
1.45. Точка движется по окружности так, что зависимость пути от времени описывается уравнением s = Bt + Сt2, где В = - 2 м/с, С = 2 м/с2. Через t1 = 1 с после начала движения нормальное ускорение точки ап = 0,5 м/с2. Найти время τ, при котором модули нормального и тангенциального ускорения будут равны.
1.46. На вал радиусом R = 10 см намотана нить, к концу которой привязана гиря. Двигаясь равноускоренно, гиря за τ = 20 с от начала движения опустилась на h = 2 м. Найти угловую скорость и угловое ускорение вала для этого момента времени.
1.47. Колесо радиусом R = 0,1 м вращается с постоянным угловым ускорением. К концу пятого оборота после начала движения линейная скорость точек обода v = 0,1 м/с. Найти: а) угловое ускорение колеса; б) тангенциальное ускорение точек обода; в) нормальное и полное ускорения точек обода через τ = 20 с движения колеса.
1.48. Твердое тело вращается с угловой скоростью 
где А = 0,5 рад/с2, В = 0,06 рад/с3. Найти для момента τ = 10с: а) модули угловой скорости и углового ускорения; б) угол между этими векторами.
1.49. Кинооператор, снимая поднимающийся самолет, вращает камеру в данный момент времени вокруг вертикальной оси с угловой скоростью ω1 и вокруг горизонтальной оси с угловой скоростью ω2 = ω1 / 5. Вокруг какой одной оси и с какой угловой скоростью вращение камеры эквивалентно этим двум ее движениям?
1.50. Круглый конус с углом полураствора α = 300 и радиусом основания R = 5 см катится равномерно без скольжения по горизонтальной плоскости (рис. 1.4). Вершина конуса закреплена шарнирно в точке О, которая находится на одном уровне с точкой С — центром основания конуса. Скорость v точки С равна 0,1 м/с. Найти: а) модули векторов угловой скорости и углового ускорения конуса; б) угол, который составляет вектор угловой скорости с вертикалью.