Примеры решения задач

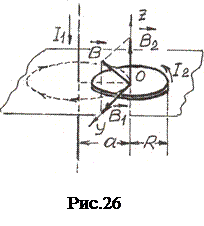
Пример 12. Длинный прямой провод, по которому протекает ток силой 10 А, и круговой контур с током 5 А расположены так, что плоскость контура перпендикулярна проводу. Расстояние от прямого тока до центра контура равно 10 см. Радиус контура R =6 см. Определить индукцию магнитного поля в центре контура.

 

Дано: I₁ = 10 A; I₂ = 5 A; а = 10 см=0,1 м; R = 6 см=0,06 м.

Найти: В.

Решение. По принципу суперпозиции индукция магнитного поля в центре контура равна геометрической сумме индукций полей, созданных токами I₁ и I₂:

.

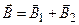Направление векторов определим по правилу буравчика (рис.26): проводим силовую линию через данную точку О, вектор индукции направляем по касательной к силовой линии.

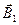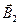Значения векторов и найдём по формулам:

· для поля бесконечно длинного проводника

;

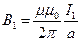· для поля в центре кругового тока

,

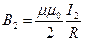где а – расстояние от бесконечно длинного проводника до точки поля О (рис.26).

Так как векторы 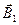и 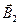взаимно перпендикулярны, то модуль результирующего вектора находим по теореме Пифагора:

= .

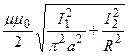Проверим размерность:

Тл.

Произведя подстановку величин 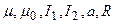получим:

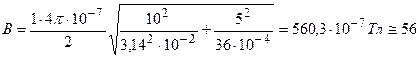мкТл

Ответ: В = 56 мкТл.

Пример 11. Короткая катушка площадью поперечного сечения 150 см², содержащая 200 витков провода, по которому течет ток силой 4 А, помещена в однородное магнитное поле напряженностью 8000 А/м. Найти магнитный момент катушки, вращающий момент, действующий на катушку со стороны поля, если ось катушки составляет с линиями индукции поля угол 60⁰.

Дано: S=150 см² =150∙10^{-4 м2} =15∙10^-3 м²; N=200; I=4 A; Н=8000 А/м; j = 60⁰.

Найти: Р_m; М.

Решение. Магнитный момент витка с током:

,

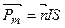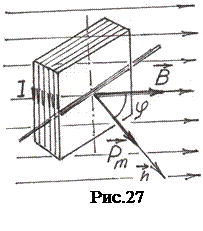
магнитный момент 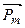- вектор, направление которого указано на рис.27.

Модуль магнитного момента катушки, содержащей N витков, площадью S:

P_m=ISN (1)

На катушку с током, помещенную в магнитное поле, действует момент сил:

M = P_m·B·sin =P_m×μ₀×μ×H×sinφ (2)

где В – индукция магнитного поля, В = mm₀Н; - угол между направлением и вектором 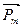, рис.27; μ₀ – магнитная постоянная; μ=1( считаем, что катушка находится в вакууме).

Выполним вычисления:

P_m=NIS=200× 4×150×10^-4=12 А×м²,

M = P_m·mm₀Н ·sin = 12×4p×10^-7×1×8000×sin60⁰ = 0,1 Н×м.

Ответ: P_m = 12 A·м²; M = 0,1 Н×м.

Пример 12. Протон, прошедший ускоряющую разность потенциалов , влетает в вакууме в однородное магнитное поле с индукцией и начинает двигаться по окружности. Вычислить: 1) радиус 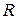окружности, описываемой протоном в поле; 2) частоту 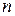вращения протона в магнитном поле.

Дано: ; ; ; .

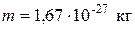Найти: , .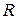

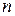Решение. Протон попадает в магнитное поле, имея скорость 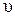, которую он приобрел, ускоряясь в электрическом поле. Скорость протона задана через ускоряющую разность потенциалов. По закону сохранения и превращения энергии работа сил электрического поля равна изменению кинетической энергии протона:

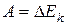
или

,

где 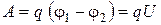– работа сил электрического поля по перемещению заряженной частицы (протона) в поле; 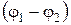– ускоряющая разность потенциалов или ускоряющее напряжение 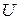; 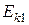и 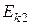– начальная и конечная кинетические энергии протона.

Пренебрегая начальной кинетической энергией 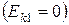и выразив кинетическую энергию через скорость, получим

,

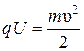откуда выразим скорость протона:

 

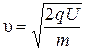. (1)

На влетевший в магнитное поле протон действует сила Лоренца

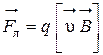. (2)

Направление силы Лоренца определяется правилом левой руки (рис. 24). Модуль силы Лоренца равен

. (3)

Так как сила перпендикулярна к скорости 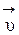, она изменяет лишь направление вектора скорости, но не его модуль, т.е. сообщает протону нормальное (центростремительное) ускорение . Под действием этой силы протон будет двигаться по окружности в плоскости, перпендикулярной линиям магнитной индукции.

Согласно второму закону Ньютона:

.

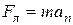Подставив сюда выражение (3) и 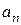, получим

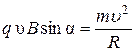, (4)

где 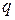, , 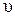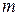– заряд, скорость, масса протона; 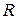– радиус кривизны траектории; – угол между направлениями векторов 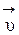и (в нашем случае , ).

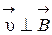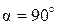Из формулы (4) выразим радиус 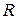окружности, учтя, что :

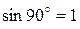. (5)

Подставив в формулу (5) выражение для скорости (1), получим:

. (6)

Подставим в формулу (6) числовые значения физических величин и выполним вычисления:

.

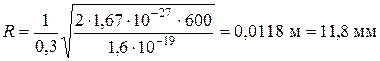Для определения частоты вращения воспользуемся формулой, связывающей частоту со скоростью и радиусом кривизны траектории:

; ; ,

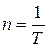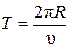где Т – период вращения.

Подставив 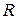из выражения (5) в формулу для частоты, получим

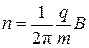. (7)

Выполним вычисления:

.

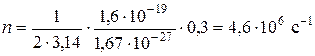Ответ: ; .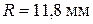

 

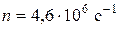Пример 13.В однородном магнитном поле с индукцией 1 Тл равномерно вращается рамка, содержащая 1000 витков. Площадь рамки 150 см², рамка делает 10 об/с. Вращение происходит относительно оси, лежащей в плоскости рамки. Определить мгновенное значение ЭДС, соответствующее углу поворота рамки 30⁰.

Дано: В = 1 Тл; N = 1000; S = 150 см² = 150·10^-4 м²; n = 10 об/с; α = 30⁰.

Найти: ε_i.

Решение. Мгновенное значение ЭДС индукции определяется по закону Фарадея:

, (1)

где Ψ – потокосцепление, Y = N Ф; Ф - магнитный поток, охватываемый одним витком; N – число витков.

При вращении рамки ( на рис.29 изображён только один виток рамки) магнитный поток Ф, изменяется по закону:

Ф = B∙S∙cosωt=BScosωt, (2)

где 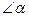- угол между нормалью к рамке и вектором , при равномерном вращении α= ωt; S – площадь, ограниченная одним витком.

При вращении рамки поток Ф периодически изменяется, в связи с этим в рамке возникает периодически изменяющаяся ЭДС индукции. .

Подставив в формулу (1) выражение потока Ф и продифференцировав по времени, получаем мгновенное значение ЭДС индукции:

= N∙B∙S∙ω∙sinωt (3)

Циклическая (круговая) частота ω связана с частотой вращения n :

ω = 2πn.

Подставив выражение ω в формулу (3) и заменив ωt на угол α, получим:

= N∙B∙S∙2π n∙sinα.

Произведем вычисление:

= 1000×1×150×10^-4×2×3,14×10×sin30⁰= 471 В.

Ответ: = 471 В.