Докажем, например, свойство 3.
Пользуясь, ассоциативностью умножения в группе, получаем
(ab)(b-1a-1) = a(bb-1)a-1 = aea-1 = aa-1=e.
Это означает, что обратным к элементу аb является b-1 а-1.
В группе однозначно, разрешимы уравнения
ах = b, уа = b. (2)
Это означает, что для каждой пары а и b существует одна и только одна пара элементов х и у, удовлетворяющих равенствам (2). Заметим, что если в полугруппе G для каждой пары элементов a,b 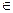 G разрешимы уравнения (2), то G является группой, то есть в G существует единица и каждый элемент имеет обратный. Итак, группу можно определить как группоид с ассоциативным умножением, в котором для каждой пары элементов а и b разрешимы уравнения (2).
G разрешимы уравнения (2), то G является группой, то есть в G существует единица и каждый элемент имеет обратный. Итак, группу можно определить как группоид с ассоциативным умножением, в котором для каждой пары элементов а и b разрешимы уравнения (2).
Определение.
Группа называется абелевой, если умножение в ней коммутативно.
Для обозначения алгебраической операции в абелевых группах принято употреблять символ +, операцию эту называют сложением, единичный элемент обозначают символом 0 и называют нулем, элемент обратный к а обозначается через –а. В связи с этим говорится о двух терминологиях в теории групп: мультипликативной, связанной с термином умножение для обозначения групповой операции и употребляемой в неабелевых группах и в общей теории групп и о терминологии аддитивной, связанной с термином сложения для обозначения групповой операции и употребляемой обычно в абелевых группах. Аддитивная (сложение) используется для обозначения групповой операции, употребляемых обычно в абелевых группах.
В группе справедлив закон сокращения: из ab = ac 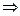 b = c и из
b = c и из
ba = ca 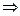 b = c.
b = c.
Группа, состоящая из конечного числа элементов, называется конечной, а число ее элементов – порядком группы. Можно доказать, что для того чтобы конечная полугруппа была группой, достаточно, чтобы в ней выполнялся закон сокращения. Рассмотрим примеры групп:
1) Каждое из множеств: Z, Q, R, C, рассматриваемое со сложением, в качестве операции образует группу; это соответственно: группа аддитивная целых рациональных, действительных и комплексных чисел. Единичным элементом каждой из этих групп является число 0. Элементом обратным к а является число –а, все они абелевы, бесконечны. Группу относительно сложения образуют так же все четные числа, а не нечетные – не образуют группы по сложению.
2) Множества Q, R, C каждое взятое без нуля образуют группы по отношению к умножению чисел. Те же множества с нулем не являются группами по отношению к умножению (нуль не имеет обратного элемента). Все эти группы абелевы и бесконечны. Единицей в каждой из них является число 1, обратным к числу а является 1/a.
3) Число 0 образует группу относительно сложения чисел. Число 1 является группой по отношению умножения. Обе они конечные, порядка 1, абелевы.
4) Числа 1 и -1 с умножением в качестве алгебраической операции образуют абелевую группу второго порядка.
Абелевой группой является так же множество {1, -1, i, -i}, если в качестве операции рассматривать умножение комплексных чисел. Вообще множество корней n степени из 1 являются группой, если в качестве операции рассматривать их умножение.
5) Группа, заданная таблицей называется группой Клейна четвертого порядка (Ф.Клейн выдающийся немецкий математик второй половины 19 и начала 20 века).
Таблица 1.
| е | а | b | c | |
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
Она абелева и в ней каждый элемент обратен себе.
Можно показать, что множество всех взаимнооднозначных отображений, некоторого множества на себя является группой относительно их суперпозиции. Если, в частности, Х является конечным множеством, то его взаимнооднозначные отображения на себя называются подстановками.
Пусть Х состоит из n элементов так как их природа не играет никакой роли, можно считать, что этими элементами считаются числа 1, 2, … , n. Тогда некоторую подстановку σ множества Х удобно представить в форме:
σ = 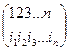 , (3)
, (3)
где в верхнем ряду записаны элементы множества Х не (обязательно в их естественном порядке), а в нижнем - образы соответствующих элементов. Например
 , (4)
, (4)
представляет собой некоторую подстановку множества, состоящего из шести элементов. Единицей группы является тождественная подстановка
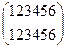 .
.

Подстановкой обратной к (3), будет
 .
.
В частности, для подстановки (4) обратной будет
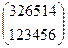 =
= 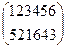 .
.
Следующий пример иллюстрирует способ умножения подстановок:
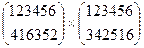 =
= 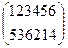 .
.
Первая подстановка переводит 1 в 4, вторая 4 в 5 итак в результате их обеих 1 переходит в 5. Аналогично 2 в1, потом окончательно 1 переходит в 3 и так далее.