Примеры распределений дискретной случайной величины

1. Биномиальное распределение.

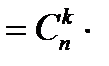
Распределение вероятностей, определяемое формулой Бернулли , называется биномиальным (см. пример 1).

2. Распределение Пуассона.

Пусть проводятся испытания по схеме Бернулли, причем велико, а вероятность 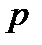мала ( ) и . В этих случаях формула Бернулли непригодна, поэтому прибегают к асимптотической формуле Пуассона

.

Эта формула выражает закон распределения Пуассона вероятностей массовых и редких событий.

Пример 3.Прядильщица обслуживает 1000 веретен. Вероятность обрыва нити на одном веретене в течение 1 мин равна 0,004. Найти вероятность того, что в течение 1 мин обрыв произойдет на 5 веретенах.

Решение. По условию, , , . Найдем :

.

С помощью таблицы найдем значение при и : .

Искомую вероятность можно найти непосредственно по формуле Пуассона:

.●

3. Геометрическое распределение.

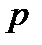Пусть производятся независимые испытания, в каждом из которых вероятность появления события постоянна иравна .Как толькособытие появляется, испытание прекращается.

Найдем закон распределения случайной величины – числа испытаний до первого появления события .

Пусть в первых испытаниях событие не появилось, а в -ом испытании появилось. Вероятность этого сложного события, по теореме умножения вероятностей независимых событий, равна

.

Ряд распределения имеет вид:

				…		…
				…		…

Вероятности образуют геометрическую прогрессию со знаменателем . Поэтому это распределение называют геометрическим.

Пример 4.Найдем вероятность появления шести очков при третьем бросании игральной кости.

Решение. Имеем , , .

.

§4.. Непрерывные случайные величины

Определение. Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Число значений дискретной случайной величины бесконечно.

Для непрерывной случайной величины нельзя перечислить все ее значения

Пусть – действительное число.

Определение. Функцией распределения (интегральной функцией) называют функцию , определяющую вероятность того, что случайная величина в результате испытания примет значение меньшее , т.е. .

Тогда непрерывную величину можно определить следующим образом:

Непрерывной называют случайную величину, функция распределения которой есть непрерывная, кусочно дифференцируемая функция с непрерывной производной.

Свойства функции

1.^о .

2.^о –неубывающая функция.

Следствие 1. .

Следствие 2.. , отсюда

3.^о Если , то при и при .

Пример 5. Непрерывная случайная величина задана функцией распределения

Найти вероятность .

Решение. .●

Определение. Плотностью распределения вероятностей непрерывной случайной величины называют функцию – первую производную от функции распределения:

.

Пример 6.Найтиплотность распределения случайной величины ,заданнойфункцией распределения

Решение. ,значит

Теорема. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в пределах от до :

. (1)

Так как или , то подставляя в формулу (1) и , получим

.

Таким образом, зная плотность распределения, можно найти функцию распределения.

Пример 7.Дана плотность распределения случайной величины .Найтифункцию распределения и вероятность попадания значения случайной величины в интервал :

Решение.

.

.●

Свойства функции

1.^о .

2.^о .

Если , то .