Составить программу для вычисления таблицы значений функции

f(x) для x [a, b] с заданным шагом изменения x

№ п/п	f (x)	a	b	Шаг
				0,1
				0,1
				0,2
				0,2
		-5	-1	0,4
		-5	-1	0,4
				0,2
				0,2
				0,1
				0,1
				0,1
				0,1
				0,2
				0,2
				0,05
				0,05
				0,2
				0,2
				0,1
				0,1
				0,05
				0,05
				0,5
				0,5
		-3	-1	0,1
		-3		0,1
				0,1
				0,2
				0,1
				0,1

 

 

10. Составить программу для вычисления элементов вектора X по формуле

10.1) х_i = ln |x_i-1| + , i = 3,4, … , n

10.2) х_i = sin³x_i-1 + , i = 3, 4, … ,m

10.3) х_i = i = 3, 4, … , n

10.4) x_j = + + , j = 3, 4, … , m

10.5) x_k = , k = 3, 4, ... , 12

10.6) х_i = i · x_i-1 + ln |x_i-1| -1, i = 2, 3, ... , k

10.7) x_j = sin + , j = 3, 4, … , n

10.8) х_i = + , i = 2, 3, ... , 20

10.9) x_k = - ln |x_k-1|, k = 2, 3, ... , m

10.10) x_j = cos² x_j-1 – tg x _j-1, j = 2, 3, … , 15

10.11) х_i = + 3 ln |x_i-1|, i = 2, 3, ... , n

10.12) x_k = tg(x_k-1-x_k-2)+ , k = 3, 4, ... , 10

10.13) x_j = + + , j = 4, 5, … , m

10.14) x_k = sin³ x_k^/_-1 + cos x + , k = 3, 4, ... , 15

10.15) x_k = cos x - ln |x_k-1|, k = 2, 3, ... , n

10.16) x_j = cos x_j-1+ sin² x_j-2+ , j = 4, 5, … , 20

10.17) х_i = , i = 2, 3, ... , n

10.18) x_k = e^x + sin²x_k-1, k = 3, 4, ... , m

10.19) x_k = sin² x_k-1+ , k = 3, 4, ... , n

10.20) x_j = +sin³x_j-1, j = 2, 3, … , 15

10.21) х_i = sin x_i-4 · cos x_i-2, i = 3, 4, ... , n

10.22) x_k = (k-1) · sin k · x_k-1 + (k-2) · sin x_k-2, k = 3, 4, ... , 20

10.23) х_i = cos x_i-1 + cos x_i-2, i = 3, 4, ... , m

10.24) x_j = cos² x_j-1+ , j = 2, 3, … , n

10.25) x_k = x_k-1 + sin x_k-2 + , k = 4, 5, ... , 15

10.26) х_i = x_i-1 · sin x_i-2, i = 3, 4, ... , m

10.27) x_k = , k = 3, 4, ... , n

10.28) x_j = , j = 2, 3, … , 20

10.29) х_i = sin + cos , i = 3, 4, ... , m

10.30) x_k = cos² x_k-2+ cos x_k-1 + x_k-3, k = 4, 5, ... , n.

11. Составить программу для вычисления суммы

№	Выражение	№	Выражение
			, i = 2, 4, 6 .... , 16
	, k= 2, 4, 6, ... , 20		, i = 1, 3, 5, ... , 19
			, k = 3, 5, ... , 15
	, k= 2, 4, 6, ... , 20
			, k = 3,5,7, ... ,17
			, i = 3,5, ... , 15
			, i = 2, 5, 8, ... , 20

 

12. Составить программу для вычисления произведения

№ п/п	Выражение	№ п/п	Выражение
			, i = 2, 4, 6, ... , 16
	, i = 2, 4, 6, ... , 20
	, i = 3, 6, 9, ... , 21		, i = 3, 5, 7, ... , 17
	, i = 2, 4, 6, ... , 20
			, i = 3,6,9,...,15
	, i = 1, 3, 5, ... , 15		, i = 3, 5, 7, ... , 17
	, k = 1, 3, 5, ... , 15
	, i = 2, 4, ... , 16		, i = 3, 5, 7, ... , 15
	, k = 2, 6, 10, ... , 22		, j = 1, 3, 5, ... , 15

 

 

13. Составить программу для вычисления величины S по формуле

№ п/п	Выражение	№ п/п	Выражение
	S =		S =
	S = sin		S = +
	S =		S =
	S =		S =
	S = 5		S = +1
	S = +e		S =
	S = ln		S =
	S = 2·		S =
	S = e + e		S =
	S = ln		S =
	S =		S =1-e
	S =1+e		S =
	S =		S =e +e
	S =		S = +ln
	S =		S =

14. Составить программу для вычисления элементов матрицы Y по известным элементам вектора X.

 

№ п/п	Выражение	№ п/п	Выражение
	yi j = ln i, j = 1, 2, ... , 10		yi j = i, j = 1, 2, ... , k
	yi j = , если xi › xj; yi j = в противном случае; i, j = 1, 2, ... , n		yi j = , если xi ›0 и xj›0; yij = в противном случае; i, j = 1, 2, ... , n
	i, j = 1, 2, ... , 15		i, j = 1, 2, ... , n
	, если sin xi › sin xj; в противном случае; i, j = 1, 2, ... , n		, если xi › 1 или xj › 1; в противном случае; i, j = 1,2, ... , n
	i, j = 1, 2, ... , 20		i, j = 1, 2, ... , m
	i, j = 1, 2, ... , k		i, j = 1, 2, ... , 10
	, если xj ≠ 0 и xi › 0; yij = в противном случае; i, j = 1,2, ... , n		yi j = ,если xi › xj; yij= в противном случае; i, j = 1,2, ... , n
	i, j = 1, 2, ... , m		i, j = 1, 2, ... , 15
	, если xi › 1 и xj › 5; в противном случае; i, j = 1, 2, ... , m		, если xi › 0 и |xj| › 1,5; в противном случае; i, j = 1, 2, ... , m
	i, j = 1, 2, ... , n		i, j = 1, 2, ... , 20
	, если i ‹ j или xi · xj › 0; в противном случае i, j = 1, 2, ... , n		, если xi ≠ 0 и xj ≠ 0; yij = 1 в противном случае i, j = 1, 2, ... , k
	i, j = 1, 2, ... , m		i, j = 1, 2, ... , m
	i, j = 1, 2, ... , 25		i , j = 1, 2, ... , 30
	yi j = , если i ‹ j; в противном случае; i, j = 1, 2, ... , n		, если i ‹ j или › 2; в противном случае; i, j = 1, 2, ... , m
	, если xi › xj и cos xi › 0,5; в противном случае; i, j = 1, 2, ... , k		yi j = , если sin xi ≤ sin xj; в противном случае; i, j = 1, 2, ... , n

 

15. Составить программу для вычисления величины S по заданной формуле

№ п/п	Выражение	№ п/п	Выражение
	S=		S=2
	S=		S=
	S=		S=
	S=		S=
	S=		S=
	S=		S=3·10-3
	S=		S=
	S=		S=
	S= 2		S=
	S=		S=
	S=		S=
	S=		S=
	S=		S=
	S=		S=
	S=		S=

 

 

16. Составить программу для вычисления элементов одномерного массива по заданной формуле

№ п/п	Выражение	№ п/п	Выражение
	к = 1, 2, … , 10		к = 1, 2, … , 10
	к = 1, 2, … , n		к = 1, 2, … , m
	к = 1, 2, … , 20		к = 1, 2, … , m
	к = 1, 2, … , m		к = 1, 2, … , n
	к = 1, 2, … , 15		к = 1, 2, … , 10
	к = 1, 2, … , 10		к = 1, 2, … , m
	к = 1, 2, … , n		к = 1, 2, … , 20
	к = 1, 2, … , m		к = 1, 2, … , n
	к = 1, 2, … , n		к = 1, 2, … , 20
	к = 1, 2, … , n		к = 1, 2, … , m
	к = 1, 2, … , n		к = 1, 2, … , 10
	к = 1, 2, … , n		к = 1, 2, … , 15
	к = 1, 2, … , n		к = 1, 2, … , m
	к = 1, 2, … , 10		к = 1, 2, … , m
	к = 1, 2, … , m		к = 1, 2, … , n

17. Используя нестандартные функции, составить программы для расчета указанных величин.

№ п/п	Выражение	№ п/п	Выражение
	, , где		где
	, , где ,		где
	где		где
	где		где
	где		где
	где		где
	, где		где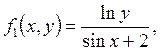
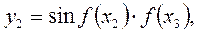	где		, где
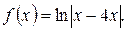
	где		где
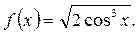
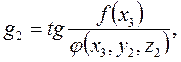	где		, где
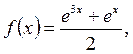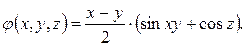
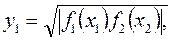	где		где
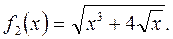
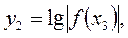	где		где
	где		где
	где		где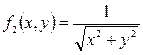
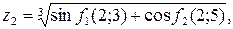	где		где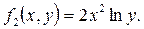