Плоских электромагнитных волн
Комплексные амплитуды этих волн связаны с комплексной амплитудой падающей волны коэффициентами отражения
 ,
, 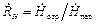
и коэффициентами преломления (прохождения)
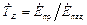 ,
,  .
.
Могут быть также введены коэффициенты отражения и преломления для среднего значения плотности потока мощности:
 ,
,  .
.
Если вектор Пойнтинга падающей волны перпендикулярен границе раздела, то
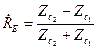 ,
,
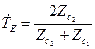 ,
,
где  – характеристическое сопротивление среды с падающей волной,
– характеристическое сопротивление среды с падающей волной, 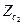 – характеристическое сопротивление среды с преломленной волной
– характеристическое сопротивление среды с преломленной волной
Из граничных условий следует, что углы падения 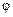 , отражения
, отражения  и преломления
и преломления 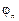 связаны законом зеркального отражения
связаны законом зеркального отражения

и законом Снелля
 , (1)
, (1)
где индекс 1 относится к среде, содержащей падающую волну. С учетом выражения для коэффициента фазы  (1) можно представить в виде
(1) можно представить в виде
 .
.
Коэффициенты отражения R и преломления Т для параллельной поляризации
 ;
;
 ;
;
для перпендикулярной
 ;
;
 .
.
При стремлении 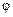 к нулю коэффициенты не зависят от ориентации вектора
к нулю коэффициенты не зависят от ориентации вектора 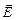 по отношению к плоскости падения. Это связано с тем, что при
по отношению к плоскости падения. Это связано с тем, что при 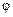 =0 понятие плоскости падения теряет смысл. Для диэлектрических сред, у которых
=0 понятие плоскости падения теряет смысл. Для диэлектрических сред, у которых 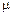 =1, коэффициенты R и Т удобно представить в более компактной форме:
=1, коэффициенты R и Т удобно представить в более компактной форме:
 ,
,
 ,
,
 ,
,
 .
.
Отраженная волна на границе раздела двух немагнитных сред не возникает. Угол падения, при котором наблюдается такое явление, называют угломБрюстера. Значение угла Брюстера для немагнитных сред находят из соотношения
 .
.
Согласно равенству (1) при  преломления больше угла падения, поэтому, если
преломления больше угла падения, поэтому, если
 ,
,
то преломленная волна будет скользить вдоль границы раздела сред.
С дальнейшим увеличением угла падения модуль коэффициентов отражения остается равным единице; будет изменяться только фаза коэффициентов R||, R^. Такое явление называют полным внутренним отражением. Можно найти, что при  =arc sin
=arc sin  коэффициенты отражения равны:
коэффициенты отражения равны:
 ,
,
 .
.
Коэффициенты преломления  и
и  при полном внутреннем отражении не равны нулю.
при полном внутреннем отражении не равны нулю.
 ,
,
если вектор Е перпендикулярен плоскости падения, и
 ,
,
если вектор 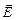 параллелен плоскости падения.
параллелен плоскости падения.
Для реальных металлов угол между фазовым фронтом и плоскостью равных амплитуд мал (см. задачу 1.27), поэтому можно полагать, что угол преломления равен нулю. Это позволяет ввести приближенное граничное условие для реальных металлов (граничное условие Леонтовича):
 или
или 
где  – единичный вектор нормали к поверхности металла, направленный внутрь; zcm=
– единичный вектор нормали к поверхности металла, направленный внутрь; zcm=  – характеристическое сопротивление металла;
– характеристическое сопротивление металла;  – касательная к поверхности металла, составляющая вектора напряженности магнитного поля.
– касательная к поверхности металла, составляющая вектора напряженности магнитного поля.
2.1. Плоская электромагнитная волна падает нормально на границу раздела между вакуумом и идеальным металлом. Амплитуда напряженности электрического поля падающей волны 0,1 В/м. Определите комплексные амплитуды напряженностей электрического и магнитного полей в вакууме на границе раздела, если вектор напряженности электрического поля падающей волны направлен по оси х декартовой системы координат с осью z, направленной перпендикулярно границе раздела вглубь металла. Записать выражения для мгновенных значений напряженностей электрического и магнитного полей в вакууме.
2.2. Плоская электромагнитная волна падает нормально на границу раздела между вакуумом и металлом с удельной электрической проводимостью 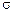 = 6·107 См/м. Определите коэффициент отражения на электрическом поле на частоте 10 ГГц, если
= 6·107 См/м. Определите коэффициент отражения на электрическом поле на частоте 10 ГГц, если  .
.
2.3. Плоская электромагнитная волна с частотой 10 МГц и средним значением плотности потока мощности 1 Вт/м надает нормально из вакуума на поверхность металла с удельной электрической проводимостью 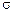 = 6·107 См/м. Определите напряженность электрического поля и среднее значение плотности потока мощности в металле непосредственно у границы раздела.
= 6·107 См/м. Определите напряженность электрического поля и среднее значение плотности потока мощности в металле непосредственно у границы раздела.
2.4. Плоская электромагнитная волна падает нормально на границу раздела между вакуумом и диэлектриком с параметрами  =4,
=4, 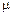 =1,
=1, 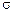 = 0. Определите среднее значение плотности потока мощности в диэлектрике, если среднее значение потока мощности падающей волны 1 Вт/м.
= 0. Определите среднее значение плотности потока мощности в диэлектрике, если среднее значение потока мощности падающей волны 1 Вт/м.
2.5. Используя эквивалентную схему в виде отрезков линии передачи, выведите формулу для коэффициента отражения по электрическому полю от диэлектрической пластины толщиной d и диэлектрической проницаемостью  при нормальном падении плоской электромагнитной волны с заданной частотой. (Потерями в пластине пренебречь.) Вычислите коэффициент отражения для
при нормальном падении плоской электромагнитной волны с заданной частотой. (Потерями в пластине пренебречь.) Вычислите коэффициент отражения для  =2,4 на длинах волн
=2,4 на длинах волн  =3,1 см и
=3,1 см и  =6,2 см, d=0,5 см.
=6,2 см, d=0,5 см.
Примечание. Воспользуйтесь формулой для входного сопротивления отрезка линии длиной d, нагруженного на сопротивление Z0.
2.6. Используя круговую диаграмму, построите распределение амплитуды электрического и магнитного полей вдоль оси, перпендикулярной пластине (см. условие задачи 2.5), пoлaгaя амплитуду напряженности электрического поля падающей волны равной 1 В/м.
2.7. Определите диэлектрическую проницаемость и толщину просветляющего покрытия на поверхности плавленого кварца для излучения с длиной волны 0,63 мкм (излучение квантового генератора на смеси неона и гелия), oбecпeчивающие равенство нулю коэффициента отражения при нормальном падении.
Примечание. Аналогом является задача о согласовании нагрузки с линией передачи через четвертьвольтовый трансформатор.
2.8. Выведите формулу для коэффициента преломления плоской электромагнитной волны, падающей нормально из вакуума на пластину толщиной d, полагая известными коэффициент распространения и характеристическое сопротивление Zc волн в пластине.
Примечание. Граничные условия на плоскостях z = 0 и z = d для двух волн слева от пластины и внутри нее и одной прошедшей волны справа.
2.9. Используя результат задачи 2.8, вычислите коэффициент преломления поля пластины керамики титанат бария (Ва Тi O3) на частоте 10 ГГц, если  =144,
=144, 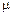 =1, tg
=1, tg  =0,6, d=0,1 мм.
=0,6, d=0,1 мм.
2.10. Плоская электромагнитная волна, распространяющаяся в вакууме, падает нормально на пластину диэлектрика толщиной d с отрицательным значением относительной диэлектрической проницаемости  . Используя результат задачи 2.8, выведите формулу для коэффициента преломления
. Используя результат задачи 2.8, выведите формулу для коэффициента преломления  . Вычислите
. Вычислите  для
для  = –1, d=1 см на частоте 10 ГГц.
= –1, d=1 см на частоте 10 ГГц.
2.11. Найдите условия, при которых плоская электромагнитная волна будет распространяться путем отражения от двух безграничных пластин идеального металла, расположенных в вакууме параллельно друг другу на расстоянии a, если угол падения равен  . Для каких значений
. Для каких значений 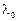 возможно распространение волн в такой структуре при заданном а?
возможно распространение волн в такой структуре при заданном а?
2.12. Определите направление переноса энергии, ориентацию и скорость движения фазового фронта  для условий задачи 2.10. Вычислите
для условий задачи 2.10. Вычислите  для
для 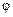 =45°.
=45°.
2.13. Определите скорость движения фазового фронта вдоль зазора между двумя параллельными бесконечными пластинами идеального металла (см. задачу 2.11). Изобразите зависимость фазовой скорости от длины волны 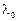 для нескольких значений m. Объясните полученный результат.
для нескольких значений m. Объясните полученный результат.
2.14. Плоская электромагнитная волна, вектор напряженности электрического поля которой лежит в плоскости падения, падает из вакуума на поверхность диэлектрика с диэлектрической проницаемостью  под углом
под углом 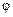 =arc tg
=arc tg  . Найдите соотношение между векторами Пойнтинга падающей и прошедшей волн. Обсудите полученный результат с точки зрения закона сохранения энергии.
. Найдите соотношение между векторами Пойнтинга падающей и прошедшей волн. Обсудите полученный результат с точки зрения закона сохранения энергии.
2.15. Плоская электромагнитная волна, вектор напряженности электрического поля которой лежит в плоскости падения, падает из диэлектрика с параметрами  на поверхность диэлектрика с параметрами
на поверхность диэлектрика с параметрами  . При каких углах падения: а) вся энергия падающей волны переходит во вторую среду; б) вся энергия падающей волны отражается от границы раздела?
. При каких углах падения: а) вся энергия падающей волны переходит во вторую среду; б) вся энергия падающей волны отражается от границы раздела?
2.16. Плоская электромагнитная волна с круговой поляризацией падает из вакуума на поверхность плавленого кварца. Определите угол падения, при котором осуществляется преобразование круговой поляризации в линейную.
2.17. Плоская электромагнитная волна с круговой поляризацией падает из вакуума под углом 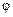 на границу раздела со средой, показатель преломления которой равен 1,531. Найдите вид поляризации отраженной волны для углов падения 0°, 45°, 56° 51'.
на границу раздела со средой, показатель преломления которой равен 1,531. Найдите вид поляризации отраженной волны для углов падения 0°, 45°, 56° 51'.
2.18. Найдите вид поляризации преломленной волны для углов падения 20, 45, 60 и 80°, если плоская электромагнитная волна, падающая на границу раздела между вакуумом и средой с показателем преломления п=1,5, имеет круговую поляризацию.
2.19. Плоская электромагнитная волна падает на границу раздела сред с различными значениями относительной магнитной проницаемости. Будет ли существовать угол, при котором отсутствует отраженная волна? Если да, то как величина этого угла связана с параметрами сред?
2.20. Вычислите угол полного внутреннего отражения для следующих диэлектриков: дистиллированной воды (  =81), слюды (
=81), слюды (  =6) оптического стекла (
=6) оптического стекла (  =2,25), полупроводника (
=2,25), полупроводника (  =16).
=16).
2.21. Плоская электромагнитная полна, распространяющаяся в среде с параметрами  =2,25,
=2,25, 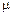 =1,
=1, 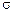 =0, падает под углом 45° на границу раздела между средой и вакуумом. Определите коэффициент отражения для волн, поляризованных в плоскости падения и перпендикулярно ей.
=0, падает под углом 45° на границу раздела между средой и вакуумом. Определите коэффициент отражения для волн, поляризованных в плоскости падения и перпендикулярно ей.
 2.22. Призма используется для поворота пучка
2.22. Призма используется для поворота пучка
электромагнитных волн. Определите комплексный коэффициент передачи устройства, т. е. отношение комплексных амплитуд напряженности электрического поля входящей и выходящей волн на передней грани призмы, принимая во внимание только однократные отражения. Показатель преломления материала призмы примите равным 1,5.
2.23. Каким показателем преломления должна обладать среда, чтобы в результате однократного полного внутреннего отражения на границе ее раздела с вакуумом можно было преобразовать волну с линейной поляризацией в волну с круговой поляризацией?
2.24. Электромагнитная волна, вектор напряженности электрического поля которой образует угол 135° с плоскостью падения, отражается от границы раздела между водой (  =81) и вакуумом. Под каким углом должна падать волна, чтобы отраженная волна имела круговую поляризацию? Какая при этом будет поляризация – правая или левая?
=81) и вакуумом. Под каким углом должна падать волна, чтобы отраженная волна имела круговую поляризацию? Какая при этом будет поляризация – правая или левая?
2.25. Плоская электромагнитная волна с линейной поляризацией падает на границу раздела между средой – показателем преломления 1,5 и вакуумом. Вектор напряженности электрического поля образует с плоскостью падения угол 45°. Определите вид поляризации отражения волны, если угол падения равен 45°.
2.26. При фотографировании на фоне водной поверхности иногда применяют поляризационные фильтры (устройства, пропускающие волны только одной поляризации). Для чего служит такой фильтр и как его следует ориентировать, чтобы достигнуть желаемого результата?
2.27. Аквалангист, плывущий по дну водоема, смотрит вертикально вверх. Какую картину он будет наблюдать? На каком расстоянии от камня, лежащего на дне, он должен находиться, чтобы увидеть его, если глубина водоема 3 м, показатель преломления воды 1,33? Расстоянием между глазом и дном можно пренебречь.
2.28. Плоская электромагнитная волна, распространяющаяся в среде с показателем преломления п=1,5, надает под углом 45° на границу раздела между средой и вакуумом. Напряженность электрического поля падающей волны 1 В/м. Определите напряженность электрического поля в вакууме на расстоянии 6 см от границы раздела, если частота колебаний равна 10 ГГц, а вектор напряженности электрического поля перпендикулярен плоскости падения.
2.29. Плоская электромагнитная волна распространяется в безграничной плоскопараллельной пластине диэлектрика с  под углом
под углом  к границе раздела с вакуумом. При каких условиях волна не будет покидать пластину?
к границе раздела с вакуумом. При каких условиях волна не будет покидать пластину?
2.30. Плоская электромагнитная волна падает под углом 60° на металлическую поверхность. Найдите амплитуду напряженности электрического поля на поверхности металла, если 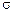 =5·107 См/м,
=5·107 См/м, 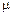 =1, f=100 ГГц, а вектор напряженности магнитного поля с амплитудой 1 А/м лежит в плоскости падения. Определите удельную мощность потерь.
=1, f=100 ГГц, а вектор напряженности магнитного поля с амплитудой 1 А/м лежит в плоскости падения. Определите удельную мощность потерь.