Формула Ньютона-Лейбница
Опираясь на свойства интеграла с переменным верхним пределом, получили основную формулу интегрального исчисления.
Теорема. Пусть функция у = f(x) непрерывна на отрезке[a, b] и F(x) – любая первообразная для f(x) на [a, b]. Тогда определенный интеграл от функции f(x) на [a, b] равен приращению первообразной F(x) на этом отрезке, т.е.
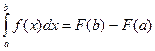 . (10)
. (10)
Доказательство: Пусть F(x) – некоторая первообразная для функции f(x). Но по теореме 2 функция Ф(х),заданная формулой Ф(х) = 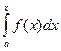 =
= 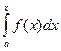 , также является первообразной для функции f(x), и найдется такое число C, что F(x) = Ф(x) + C. Тогда для приращения первообразной имеем
, также является первообразной для функции f(x), и найдется такое число C, что F(x) = Ф(x) + C. Тогда для приращения первообразной имеем
F(b) – F(a) = (Ф(b)+C) – (Ф(a)+C) =Ф(b) – Ф(а) =  -
-  .
.
Но  . И тогда F(b) –F(a) =
. И тогда F(b) –F(a) =  .
.
Нахождение определенных интегралов с использованием формулы Ньютона-Лейбница осуществляется в два шага: на первом шаге, используя технику нахождения неопределенного интеграла, находят некоторую первообразную F(x) для подынтегральной функции f(x); на втором применяется собственно формула Ньютона-Лейбница– находится приращение первообразной, равное искомому интегралу. В связи с этим, введем обозначение для приращения первообразной, которое удобно использовать при записи решений. По определению положим
 .
.
Следует подчеркнуть, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную F(x) для подынтегральной функции f(x), например, имеющую наиболее простой вид при С=0.