Достаточное условие существования оптимального базисного решения (с обоснованием).

Определение 1. Задача математического программирования:

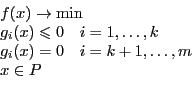
Пусть

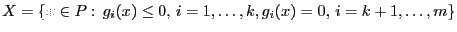
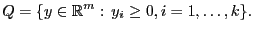
Полагаем, что 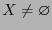. Пусть 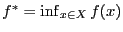. Если 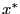--решение, то 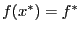, но решение не всегда существует.

Определение 2. 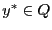называется вектором Куна--Таккера, если верно

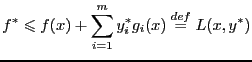(регулярная функция Лагранжа)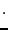

Теорема 1. Пусть 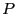-- выпуклое 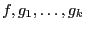-- выпуклые на 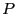, -- линейные. Пусть хоть одно из следующих двух условий выполнено:

1. .

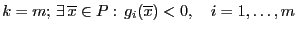2. 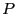-- полиэдр, 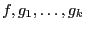-- линейны, .

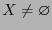Тогда существует вектор Куна--Таккера.

Определение 3. Двойственной называется задача следующего вида:

Теорема 2. Пусть существует вектор Куна--Таккера и 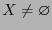. Если 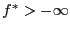, то 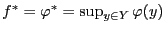и множество решений 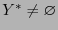и совпадает с множеством векторов Куна--Таккера.

Определение 4. Общая задача линейного программирования:

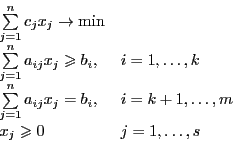
Пусть , ,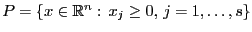

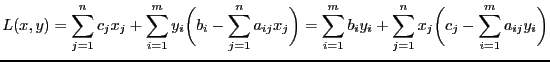
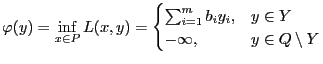
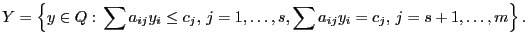
Получили двойственную задачу:

Теорема 3. Двойственная к двойственной совпадает с исходной.

Теорема 4. (критерий разрешимости задачи ЛП) Пусть 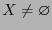и целевая функция ограничена снизу на допустимом множестве ( 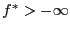). Тогда задача ЛП имеет решение.

Доказательство. По теореме 2. существует решение двойственной задачи. А по теореме 3. существует решение прямой задачи.

Определение 5. 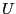-- выпуклое множество, 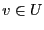называется угловой точкой этого множества, если представление этой точки в следующем виде 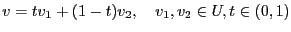возможно только в одном случае: .

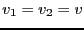Поставим задачу ЛП в канонической форме:

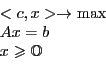
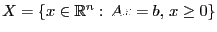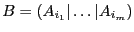Очевидно, что допустимое множество выпуклое. Будем считать, что . Мы можем выбрать ЛНЗ, а все остальные столбцы будем обозначать 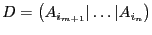. Обозначим

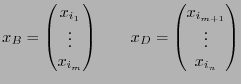
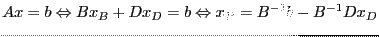
Определение 6. Переменные в 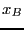называются базисными, а в 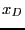-- не базисными.

Определение 7. Решение системы 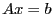называется базисным, если 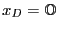, т.е. .

Определение 8. Базисом базисного решения называется совокупность столбцов , входящих в .

Определение 9. Базисное решение называется допустимым, если .

Определение 10. Допустимое базисное решение называется невырожденным, если значения базисных переменных , иначе оно вырождено.

Определение 11. называют допустимым базисным решением, если столбцы матрицы , соответствующие ненулевым координатам вектора , линейно независимы.

Базис однозначно определяет допустимое базисное решение, обратное неверно.

Теорема 5. Если 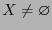, то существует допустимое базисное решение.

Теорема 6. Любое допустимое базисное решение является угловой точкой множества и наоборот.

Симплекс метод представляет собой вычислительную процедуру, осуществляющую перебор допустимых базисных решений задачи до нахождения оптимального допустимого решения. При этом на каждой итерации симплекс метода в зависимости от значений некоторых параметров делается один из трех следующих выводов:

1. рассматриваемое ДБР является решением задачи;

2. целевая функция неограниченно возрастает;

3. осуществляется переход к новому допустимому базисному решению с нехудшим значением целевой функции.

Описание одной итерации симплекс метода. Пусть известно некоторое ДБР. . образуют базис точки . Будем рассматривать матрицу базисных столбцов и соответствующие , введенные по аналогии.

т.к.

Для имеем .

Задача переписывается в следующем виде:

Пусть .

Всю информацию о коэффициентах принято записывать в виде симплекс таблицы.

Как меняются переменные? Рассмотрим . . Мы хотим выбрать номер небазисной переменной и ее значение так, чтобы точки, получающиеся по этим формулам, удовлетворяли всем ограничениям задачи и при этом . Возможны три случая:

1) . Покажем, что в этом случае точка -- решение. Рассмотрим .

Это неравенство следует из неотрицательности .

т.е. -- решение.

2) . Тогда задача не имеет решения.

Рассмотрим . (т.к. мы пользовались формулами перехода), т.е. . .

3) . Можем перейти к новому ДБР с нехудшим значением целевой функции.

Пусть достигается на . Построим новую точку по формулам пересчета. . . .

Теорема 7. Точка является допустимым базисным решением, базисом будут столбцы и .

18. Неоднозначность терминологии ЛП: понятия матрица и вектор условий задачи ЛП, опорный план и оптимальный план задачи ЛП.

Основные понятия и обозначения. Пусть m и n два произвольных натуральных числа.Матрицей размера m на n (записывается так )называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа -номер строки и номер столбца.

Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами: - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом

Приведём некоторые обозначения, которыми будем пользоваться в дальнейшем:

- множество всех матриц размера m на n;

- матрица A с элементами в позиции (i,j);

- матрица размера m на n.

Элементы , где i=j, называются диагональными, а элементы , где - внедиагональными. Совокупность диагональных элементов , где k = min (m,n), называется главной диагональю матрицы.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается символом O.

Заметим, что для каждого размера существует своя нулевая матрица.

Матрица размера n на n называется квадратной матрицей n-го порядка, т.е. число строк равно числу столбцов.

Квадратная матрица называется диагональной, если все ее внедиагональные элементы равны нулю.

Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной матрицей и обозначается символом I или E.

Матрица размера называется матрицей-строкой или вектор-строкой. Матрица размера называется матрицей столбцом или вектор-столбцом.