Пример 1.
Используя элементарные преобразования строк преобразовать матрицу A в верхнюю треугольную матрицу, где
| A = | 
| 
| |||
| -1 |
Решение:
поменяем первую и вторую строку местами

| 
| ~ | 
| 
| ~ | ||||||
| -1 | -1 |
ко 2-рой строке прибавим 1-вую, умноженную на -4; к третей строке прибавим первую
| ~ | 
| 
| ~ | 
| 
| ~ | ||||||
| 4 + (-4)·1 | 2 + (-4)·3 | 0 + (-4)·2 | -10 | -8 | ||||||||
| -1 + 1 | 3 + 3 | 10 + 2 |
2-рую строку поделим на -2, третью строку делим на 6
| ~ | 
| 
| ~ | 
| 
| ~ | ||||||
| -10/(-2) | -8/(-2) | |||||||||||
| 6/6 | 12/6 |
поменяем вторую и третью строку местами
| ~ | 
| 
| ~ | |||
к 3-тей строке прибавим 2-рую, умноженную на -5
| ~ | 
| 
| ~ | 
| 
| ||||||
| 5 + (-5)·1 | 4 + (-5)·2 | -6 |
1. Определители, их вычисление, свойства, применение (определения; способы вычисления определителей 2-го и 3-го порядка; алгебраические дополнения к элементам определителя). Примеры.
1)Определение.
Квадратной матрице А порядка n можно сопоставить число det А (или |A|, или 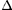 ), называемое ее определителем, следующим образом:
), называемое ее определителем, следующим образом: 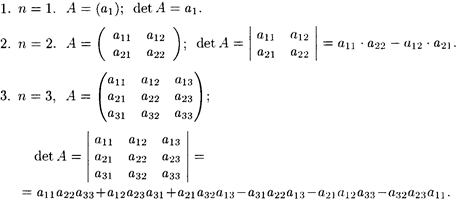
Определитель матрицы A также называют ее детерминантом.
2)Вычисление .
определителя 2-го порядка иллюстрируется схемой: 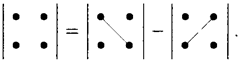
Пример 4.1.
Найти определители матриц

Решение:
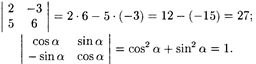
При вычислении определителя 3-го порядка пользуются правилом треугольников (или Саррюса):
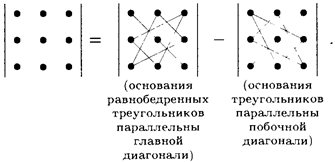
Пример 4.2.
Вычислить определитель матрицы
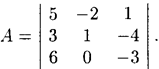
Решение:
det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.
3)СВОЙТСВА.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами, 
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно, 
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
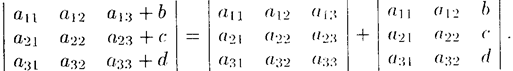
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.
Пример 4.3.

Решение: Действительно, используя свойства 5, 4 и 3 получим 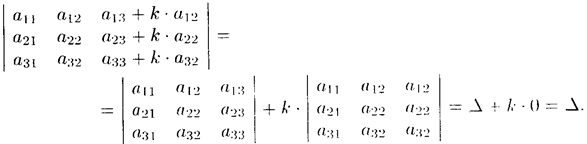 Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента аij определителя n-го порядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij  Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком
Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком
«минус», если эта сумма нечетная. Обозначается Aij :
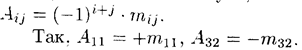
Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что 
В самом деле, имеем
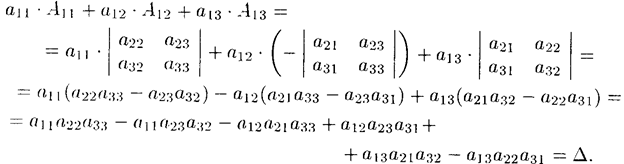 Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Пример 4.4.
Вычислите определитель матрицы

Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю. 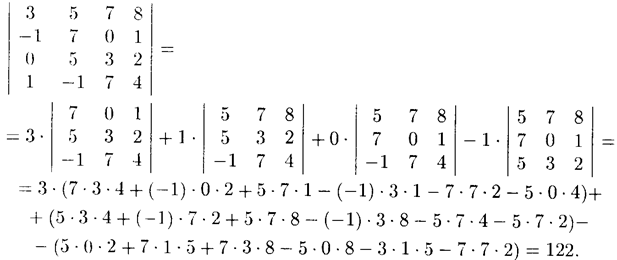
Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например, 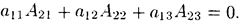
2. Ранг матрицы (определение). Операции, применяемые при вычислении ранга матрицы. Примеры.
1)Определение
Минором порядка 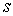 матрицы
матрицы 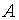 называется определитель квадратной матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких-либо выбранных
называется определитель квадратной матрицы, образованной из элементов исходной матрицы, находящихся на пересечении каких-либо выбранных 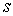 строк и
строк и 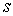 столбцов матрицы
столбцов матрицы 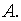
В матрице 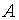 порядка
порядка  минор порядка
минор порядка 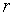 называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе.
называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не существуют вовсе.
Порядок базисного минора матрицы 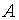 называется рангом матрицы и обозначается символом
называется рангом матрицы и обозначается символом 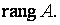
Замечание. Из приведённых определений следует, что ранг матрицы равен наибольшему из порядков её миноров, отличных от нуля.
Одним из способов вычисления ранга матрицы является метод окаймления миноров.
Пример. Определить ранг матрицы
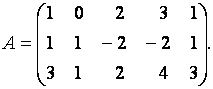
Среди миноров второго порядка матрицы 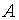 существует, по крайней мере, один, отличный от нуля. Например, минор матрицы
существует, по крайней мере, один, отличный от нуля. Например, минор матрицы 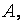 полученный вычёркиванием из этой матрицы третьей строки, третьего, четвёртого и пятого столбцов, отличен от нуля:
полученный вычёркиванием из этой матрицы третьей строки, третьего, четвёртого и пятого столбцов, отличен от нуля:

Следовательно, ранг данной матрицы не меньше двух.
Найдём миноры третьего порядка матрицы  Все десять миноров третьего порядка равны нулю, поэтому ранг данной матрицы не может быть равен трём. Таким образом,
Все десять миноров третьего порядка равны нулю, поэтому ранг данной матрицы не может быть равен трём. Таким образом, 
Другой способ вычисления ранга матрицы основан на применении элементарных преобразований матрицы и использовании следующих утверждений.
Теорема 4.1. Ранг ступенчатой матрицы равен количеству её ненулевых строк.
Теорема 4.2. Элементарные преобразования матрицы не изменяют её ранг.
Пример. Вычислим ранг матрицы из предыдущего примера. Для этого матрицу 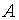 с помощью элементарных преобразований приведём к ступенчатому виду. Найдём сумму второй строки матрицы
с помощью элементарных преобразований приведём к ступенчатому виду. Найдём сумму второй строки матрицы 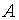 с первой строкой, умноженной на
с первой строкой, умноженной на 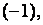 а также сумму третьей строки матрицы
а также сумму третьей строки матрицы 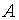 с первой строкой, умноженной на
с первой строкой, умноженной на 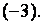 В результате указанных элементарных преобразований получим эквивалентную матрицу
В результате указанных элементарных преобразований получим эквивалентную матрицу
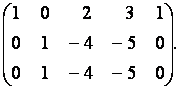
Третью строку полученной матрицы сложим с её первой строкой, умноженной на 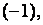 и получим эквивалентную матрицу
и получим эквивалентную матрицу 
Удалим из этой матрицы третью строку и получим ступенчатую эквивалентную матрицу, количество ненулевых строк которой равно двум: 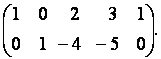
В соответствии с теоремой 4.1, ранг полученной матрицы равен двум, а значит (теорема 4.2), 
--1)Если все миноры первого порядка (т.е. элементы матрицы A) равны нулю, то rangA=0. Если среди миноров первого порядка есть хотя бы один, не равный нулю, то rangA⩾1. Переходим к проверке миноров второго порядка.
--2)Если все миноры второго порядка равны нулю, то rangA=1. Если среди миноров второго порядка есть хотя бы один, не равный нулю, то rangA⩾2. Переходим к проверке миноров третьего порядка.
--3)Если все миноры третьего порядка равны нулю, то rangA=2. Если среди миноров третьего порядка есть хотя бы один, не равный нулю, то rangA⩾3. Переходим к проверке миноров четвёртого порядка.
--4)Если все миноры четвёртого порядка равны нулю, то rangA=3. Если среди миноров четвёртого порядка есть хотя бы один, не равный нулю, то rangA⩾4. Переходим к проверке миноров пятого порядка и так далее.
3. Обратная матрица (определение). Достаточное условие существование обратной матрицы (с доказательством). Примеры.
1.Определение.
Матрица A − 1 называется обратнойматрице A, если выполняется условие
| A · A -1 = A -1 · A = E , |
где E — единичная матрица n –ого порядка.
2.Условие существования обратной матрицы. Для того, чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы она была невырожденной, т.е. det A ≠ 0 .
Теорема 4.1. (необходимое и достаточное условие существования
обратной матрицы).
Обратная матрица A  существует тогда и только тогда, когда исходная матрица А невырожденная.
существует тогда и только тогда, когда исходная матрица А невырожденная.
Доказательство.
Необходимость. Пусть матрица А имеет обратную A  , т. е. A
, т. е. A  A
A 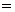 AA
AA 
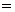 E. По свойству 10 определителей имеем D(A
E. По свойству 10 определителей имеем D(A  A)
A) 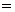 = D(A
= D(A  )D(А)
)D(А) 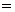 D(E) = 1 и, следовательно, D(А)
D(E) = 1 и, следовательно, D(А) 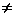 0.
0.
Достаточность. Пусть D(А) 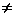 0. Рассмотрим квадратную матрицу n-го порядка
0. Рассмотрим квадратную матрицу n-го порядка 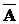 , называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы
, называемую присоединенной. Ее элементами служат алгебраические дополнения элементов матрицы 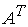 , транспонированной к матрице А:
, транспонированной к матрице А:
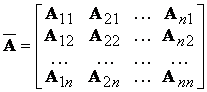 .
.
Легко показать, что
 .
.
Отсюда следует, что если в качестве обратной матрицы взять матрицу A 
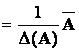 , то произведения A
, то произведения A  AиAA
AиAA  равны единичной матрицеE n-го порядка: A
равны единичной матрицеE n-го порядка: A  A
A  AA
AA 
 E.
E.
4. Обратная матрица (определение). Решение матричных
уравнений с помощью обратной матрицы. Примеры.
1.Определение.
Матрица A − 1 называется обратнойматрице A, если выполняется условие
| A · A -1 = A -1 · A = E , |
где E — единичная матрица n –ого порядка.
2.Решение матричных уравнений с помощью обратной матрицы.
Примет1.
Найти А-1, если А = 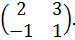
Решение: 1) Находит det A = 
2) Находим А*: А11=1, А21=-3, А12=-(-1), А22=2, поэтому А*= 
3)Находим А-1: А-1= 1/5  =
=  .
.
Проверка:
А · А-1=  ·
·  =
= 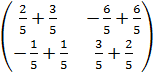 =
= 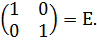
Пример2.
Показать, что матрица А является обратной для В, если
 ,
, 
Решение: 1)Найдем произведение матриц А и В:
А · В = 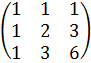 ·
·  =
=
= 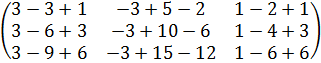
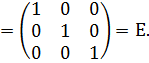
Аналогично В · А = Е. Следовательно, матрица А является обратной для В.
5. Система линейных алгебраических уравнений (определение). Совместные и несовместные СЛАУ. Теорема Кронекера-Капелли. Однородные СЛАУ. Примеры.
1.Определение.
Система линейных алгебраических уравнений (СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:

Где числа aij, i = 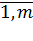 , j =
, j =  называется коэффициентами системы, числа bi – свободными числами. Подлежат нахождению числа xn.
называется коэффициентами системы, числа bi – свободными числами. Подлежат нахождению числа xn.
2.Совместные и несовместные СЛАУ.
СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Система  является совместной, так как она имеет, по крайней мере, одно решение
является совместной, так как она имеет, по крайней мере, одно решение  ,
, 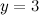
Пример
Система 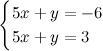 является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов
является несовместной, так как выражения, стоящие в левых частях уравнений системы равны, но правые части не равны друг другу. Ни для каких наборов 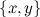 это не выполняется.
это не выполняется.
3.Теорема Кронекера-Капелли.
Пусть дана произвольная система m линейных уравнений с n неизвестными

Исчерпывающий ответ на вопрос о совместности этой системы дает теорема Кронекера-Капелли.
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг (A) расширенной матрицы системы равен рангу основной матрицы (A˜).,т.е rangA=rangA˜.
Примем её без доказательства.
Правила разыскивания всех решений совместной системы линейных уравнений вытекает из следующих теорем.
Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
ПРАВИЛО РЕШЕНИЯ ПРОИЗВОЛЬНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
1. Найти ранги основной и расширенной матриц системы. Если r(A) ≠ r( 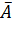 ), то система несовместна.
), то система несовместна.
Расширенной матрицей системы называется матрица, полученная из
матрицы системы, дописыванием справа после вертикальной черты столбца свободных членов.
2. Если r(A) = r( 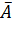 )= r, система совместна. Найти какой-либо базисный минор порядка r.Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить.) Неизвестные, коэффициенты которых входят в базисный минор, называю главными и оставляют слева, а остальные n-r неизвестных называют свободными и переносят в правые части уравнений.
)= r, система совместна. Найти какой-либо базисный минор порядка r.Взять r уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить.) Неизвестные, коэффициенты которых входят в базисный минор, называю главными и оставляют слева, а остальные n-r неизвестных называют свободными и переносят в правые части уравнений.
3. Найти выражения главных неизвестных через свободные. Получено общее решение системы.
4. Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
Пример.
Исследовать на совместность систему
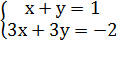
Решение:
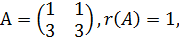
 Таким образом, r(A) ≠ r(
Таким образом, r(A) ≠ r( 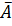 ), следовательно, система несовместна.
), следовательно, система несовместна.
4.Однородные СЛАУ.
Система называется однородной, если все правые части уравнений, входящих в нее, равны нулю одновременно.
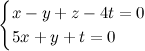
6. Системы линейных алгебраических уравнений (определение). Определенные и вырожденные СЛАУ (определение количества базисных и свободных переменных). Решение СЛАУ (общая схема). Метод Гаусса. Примеры.
1.Определение.
Система линейных алгебраических уравнений (СЛАУ), содержащей m уравнений и n неизвестных, называется система вида:

Где числа aij, i = 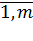 , j =
, j =  называется коэффициентами системы, числа bi – свободными числами. Подлежат нахождению числа xn.
называется коэффициентами системы, числа bi – свободными числами. Подлежат нахождению числа xn.
2.Определенные и вырожденные СЛАУ (определение базисных и свободных переменных).
Система называется определённой, если она совместна и имеет единственное решение.
Система называется вырожденной, если определитель системы равен 0 (А=0)
Если коэффициенты при r переменных совместной СЛАУ образуют базисный минор матрицы системы A, то эти r переменных называют базиснымиили основными. Остальные n-r переменных именуют свободнымиили неосновными.
3.Решение СЛАУ (общая схема).

Решением СЛАУ называют всякую упорядоченную совокупность чисел (α1,α2,…,αn), если элементы этой совокупности, подставленные в заданном порядке вместо неизвестных x1,x2,…,xn, обращают каждое уравнение СЛАУ в тождество.
4.Метод Гаусса.
Метод Гаусса включает в себя прямой (приведение расширенной матрицы к ступенчатому виду, то есть получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и называется методом Гаусса.
Задание. Решить СЛАУ методом Гаусса
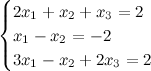
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент 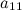 равнялся 1 (это мы делаем для упрощения вычислений):
равнялся 1 (это мы делаем для упрощения вычислений):

Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых: 
Все элементы третьей строки делим на два (или, что тоже самое, умножаем на 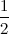 ):
):
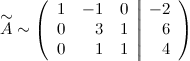
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:

От третьей строки отнимаем вторую, умноженную на 3: 
Умножив третью строку на  , получаем:
, получаем:
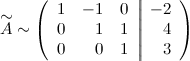
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент 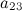 , для этого от второй строки отнимем третью:
, для этого от второй строки отнимем третью:
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую:
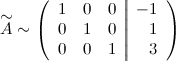
Полученной матрице соответствует система
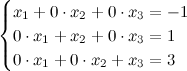 или
или 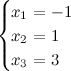
Ответ. 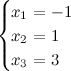
7. Системы линейных алгебраических уравнений. Определенные СЛАУ (достаточное условие единственности решения СЛАУ). Матричный метод и правило Крамера (с доказательством). Примеры.
Система называется определённой, если она совместна и имеет единственное решение.
1.Матричный метод
С помощью данного метода можно находить решение только для квадратных СЛАУ.
Запишем заданную систему в матричном виде:

Если матрица 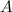 невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу
невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу  . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу
. Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу 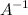 слева:
слева:

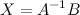
Поэтому, чтобы найти неизвестную матрицу  надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Замечание
Данный метод удобно применять тогда, когда нужно решить много одинаковых систем с разными правыми частями.
Пример.
Найти решение СЛАУ матричным методом.

Решение.
Выпишем матрицу системы 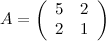 и матрицу правых частей
и матрицу правых частей 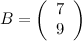 . Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму:
. Найдем обратную матрицу для матрицы системы. Для матрицы второго порядка обратную можно находить по следующему алгоритму:
1) матрица должна быть невырождена, то есть ее определитель не должен равняться нулю: 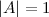 ;
;
2) элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный и делим полученные элементы на определитель матрицы. Итак, получаем, что
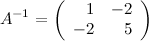
Тогда
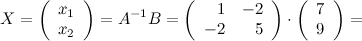

Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что  ,
, 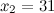
Ответ.  ,
, 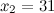
2.Правило Крамера (с доказательством).
Метод Крамера (теорема Крамера) — способ решения квадратных СЛАУ с ненулевым определителем основной матрицы.
Теорема Крамера. Если определитель матрицы квадратной системы не равен нулю, то система совместна и имеет единственное решение, которое находится по формулам Крамера:
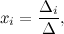
где  - определитель матрицы системы,
- определитель матрицы системы, 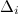 - определитель матрицы системы, где вместо
- определитель матрицы системы, где вместо 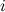 -го столбца стоит столбец правых частей.
-го столбца стоит столбец правых частей.
Замечание
Если определитель системы равен нулю, то система может быть как совместной, так и несовместной.
Замечание
Данный метод удобно применять для маленьких систем с громоздкими вычислениями, а так же если нужно найти одну из неизвестных. Трудность заключается в том, что необходимо считать много определителей.
Пример.
Найти решение СЛАУ  при помощи метода Крамера.
при помощи метода Крамера.
Решение.
Вычисляем определитель матрицы системы:
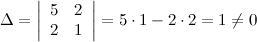
Так как 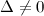 , то по теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель
, то по теореме Крамера система совместна и имеет единственное решение. Вычислим вспомогательные определители. Определитель 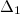 получим из определителя
получим из определителя  заменой его первого столбца столбцом свободных коэффициентов. Будем иметь:
заменой его первого столбца столбцом свободных коэффициентов. Будем иметь: 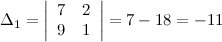
Аналогично, определитель  получается из определителя матрицы системы
получается из определителя матрицы системы  заменой второго столбца столбцом свободных коэффициентов:
заменой второго столбца столбцом свободных коэффициентов: 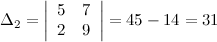
Тогда получаем, что

Ответ.  ,
, 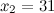
8. Вектор (геометрическое и формальное определения). Отношения между векторами (равенство, коллинеарность, перпендикулярность, компланарность). Длина и направляющие косинусы вектора (их определение в координатном представлении, теорема о направляющих косинусах). Элементарные действия с векторами (сложение, умножение на число). Примеры.
1.Определение.
Вектор – направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление.
Вектором называется направленный отрезок (формальный)
2.Отношения между векторами.
1)Равенство - Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны.
Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины:
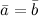 , если
, если 
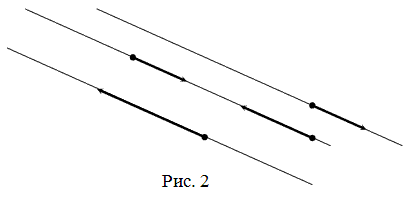
2)Коллинеарность- Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых
3)Перпендикулярность- векторы называются перпендикулярными, если угол между ними равен 90°.
4)Компланарность - Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости. 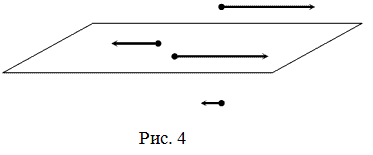
Два вектора всегда компланарны.
3.Длина и направляющие косинусы вектора
Длиной (модулем) вектора, координаты которых известны, равен корню квадратному из суммы квадратов координат. 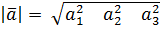
Направляющие косинусы вектора 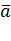 – это косинусы углов, которые вектор образует с положительными полуосями координат.
– это косинусы углов, которые вектор образует с положительными полуосями координат.
Если в пространстве задан вектор  , то его направляющие косинусы вычисляются по формулам:
, то его направляющие косинусы вычисляются по формулам: 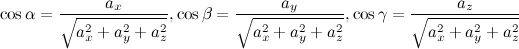
Теорема о направляющих косинусах:
cos2 α + cos2 β + cos2 γ = 1
сумма квадратов направляющих косинусов ненулевого вектора равна единице.
4)Элементарные действия над векторами.
----Суммой  векторов
векторов 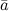 и
и 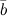 называют такой третий вектор
называют такой третий вектор 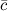 , начало которого совпадает с началом
, начало которого совпадает с началом 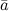 , а конец - с концом
, а конец - с концом 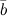 при условии, что конец вектора
при условии, что конец вектора 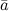 и начало вектора
и начало вектора  совпадают.
совпадают.
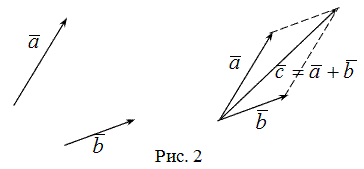
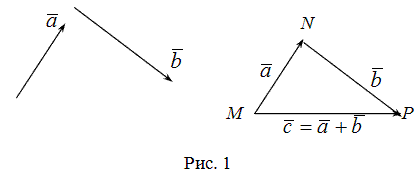
Свойства операции сложения:
1° 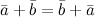 - коммутативность
- коммутативность
2° 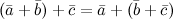 - ассоциативность
- ассоциативность
3° 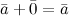
4° 
----Произведением 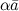 вектора
вектора 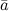 на число
на число 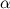 называется вектор λ ·
называется вектор λ · 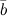 , который имеет длину
, который имеет длину  , коллинеарен вектору
, коллинеарен вектору 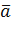 , имеет направление вектора
, имеет направление вектора 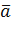 , λ
, λ  и противоположное направление, если λ
и противоположное направление, если λ  удовлетворяющие условия:
удовлетворяющие условия:
1. 
2. 
3.  , если
, если  ,
,  , если
, если  .
.
Свойства умножения вектора на число:
1. 
2. 
3. 
4. 
5. 
6. 
Здесь 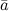 и
и 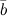 - произвольные векторы,
- произвольные векторы, 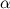 ,
,  - произвольные числа.
- произвольные числа.
11. Скалярное произведение векторов (определение, свойства и геометрический смысл). Угол между векторами, проекция вектора на направление, заданное другим вектором. Критерий перпендикулярности векторов. Примеры.
1)Скалярное произведение векторов (определение, свойства и геометрический смысл.)
Скалярным произведением двух ненулевых векторов 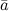 и
и 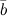 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:

ПРИМЕР.
Вычислить скалярное произведение векторов 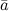 и
и 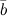 , если их длины соответственно равны 2 и 3, а угол между ними 60°.
, если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия  ,
,  , а
, а  , то
, то 
Свойства скалярного произведения.
1.  - переместительное свойство.
- переместительное свойство.
2.  =
=  -скалярный квадрат вектора.
-скалярный квадрат вектора.
3.  - распределительное свойство.
- распределительное свойство.
4.  - сочетательное свойство
- сочетательное свойство
5. Если  и
и  и
и  , то
, то  . Верно и обратное утверждение.
. Верно и обратное утверждение.
Геометрический смысл:
 ,
,
Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
2) Угол между векторами, проекция вектора на направление, заданное другим вектором.
Угол между векторами:
Пусть заданы два произвольных ненулевых вектора 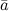 и
и 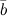 . Приведем их к общему началу, для этого отложим от некоторой точки
. Приведем их к общему началу, для этого отложим от некоторой точки  векторы
векторы  и
и  , равные соответственно заданным векторам
, равные соответственно заданным векторам 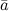 и
и 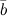 (рис. 1).
(рис. 1). 
Углом между векторами 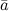 и
и 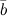 называется угол
называется угол  .
.
Проекция вектора на направление:
Проекцией вектора 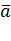 на направление вектора b , называется число, равное величине проэкции вектора
на направление вектора b , называется число, равное величине проэкции вектора 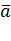 на ось проходящую через вектор b.
на ось проходящую через вектор b. 
Нахождение проекции вектора 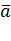 на направление, заданное вектором
на направление, заданное вектором  , может осуществляться по формуле
, может осуществляться по формуле
 , т.е.
, т.е. 
Критерии перпендикулярности векторов:
Теорема.
Для перпендикулярности двух ненулевых векторов 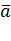 и
и  необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство формула (
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство формула (  .
.
Необходимое и достаточное условие перпендикулярности двух векторов в
координатах имеет вид  на плоскости, а в трехмерном пространстве
на плоскости, а в трехмерном пространстве 
12. Векторное произведение векторов (определение, свойства и геометрический смысл). Определение площади параллелограмма и треугольника. Критерий коллинеарности векторов. Примеры.
1)Векторное произведение векторов (определение, свойства и геометрический смысл).
Векторным произведением вектора 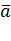 на вектор
на вектор  называется вектор
называется вектор  , который:
, который:
1)  – перпендикулярен вектору а и в.
– перпендикулярен вектору а и в.
2)  , где
, где 
3) векторы  образуют правую тройку.
образуют правую тройку.
Тройка векторов 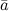 ,
, 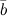 и
и 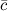 называется правой, если поворот от вектора
называется правой, если поворот от вектора 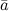 к вектору
к вектору 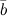 , видимый с конца третьего вектора
, видимый с конца третьего вектора 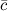 , осуществляется против хода часовой стрелки (рис. 2).
, осуществляется против хода часовой стрелки (рис. 2).
 Обозначается векторное произведение
Обозначается векторное произведение  .
.
Свойства векторного произведения:
1.  , тогда и только тогда, когда
, тогда и только тогда, когда  - коллинеарность
- коллинеарность
2.  - при перестановки сомнож. вектор. произв. Меняет знак.
- при перестановки сомнож. вектор. произв. Меняет знак.
3.  - сочетательное свойство
- сочетательное свойство
4.  -распределительное свойство.
-распределительное свойство.
Если векторы заданы своими координатами  ,
,  , то векторное произведение находится по формуле:
, то векторное произведение находится по формуле:

Пример.
Найти векторное произведение векторов  и
и 
Решение.Составляем определитель и вычисляем его: 


Геометрический смысл векторного произведения
Если векторы a и b приведены к общему началу (что параллельным переносом возможно сделать всегда, поскольку мы работаем только со свободными векторами), то длинавектора c=  равна площади параллелограмма, построенного на перемножаемых векторах (см.Рис.28).
равна площади параллелограмма, построенного на перемножаемых векторах (см.Рис.28).

2)Определение площади параллелограмма и треугольника.  ,
, 
Пример.
Вычислить площадь треугольника с вершинами  ,
, 
Решение.1. Найдем координаты векторов
 ;
;
 .
.
2.Вычислим векторное произведение  3.Найдем модуль вектора
3.Найдем модуль вектора  ,
,  .
.
Пример. Найти площадь параллелограмма, построенного на векторах  , если
, если  и угол между векторами
и угол между векторами  и
и  равен
равен  .
.
Решение.


3)Критерии коллинеарности векторов.
Если 
 .
.
13. Смешанное произведение векторов (определение, свойства и геометрический смысл). Определение объема параллелепипеда и тетраэдра. Критерий компланарности тройки векторов. Примеры.
1)Смешанное произведение векторов (определение, свойства и геометрический смысл).
Смешанным произведением трех векторов  называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на вектор
на вектор 
Геометрический смысл смешанного произведения
Если тройка векторов  правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:
правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах:  . В случае левой тройки
. В случае левой тройки  смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:
смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус:  . Если
. Если  и
и  компланарны, то их смешанное произведение равно нулю.
компланарны, то их смешанное произведение равно нулю.
Объем параллелепипеда, построенного на векторах  и
и  равен модулю смешанного произведения этих векторов:
равен модулю смешанного произведения этих векторов:
 Объем пирамиды, построенной на этой тройке векторов равен
Объем пирамиды, построенной на этой тройке векторов равен

Свойства смешанного произведения векторов:
1. СП не меняется при циклической перестановки его сомножителей: 
2. СП не меняется при перемене местами знаков векторного и скалярного умножения: 
3. СП меняет свой знак при перемене мест любых двух векторов-сомножителей:  .
.
4. СП ненулевых векторов  равно нулю тогда и только тогда, когда они компланарны.
равно нулю тогда и только тогда, когда они компланарны.
Если  , то
, то  .
.
2) Определение объема параллелепипеда и тетраэдра.
Объем параллелепипеда V, построенного на трех некомпланарных векторах  определяется по формуле:
определяется по формуле:

Объем тетраэдра, построенного на трех некомпланарных  векторах определяется по формуле:
векторах определяется по формуле: 
Пример.
Объем тетраэдра равен 1/6 объема параллелепипеда, построенного на трех некомпланарных векторах  Найдем объем параллелепипеда как модуль смешанного произведения векторов
Найдем объем параллелепипеда как модуль смешанного произведения векторов 
Тогда объем тетраэдра  .
.
3)Критерий компланарности трех векторов.
Векторы  компланарны тогда и только тогда, когда их смеш. Произв. Равно нулю
компланарны тогда и только тогда, когда их смеш. Произв. Равно нулю  :
:
 векторы
векторы  компланарны.
компланарны.
14. Задача разложения вектора по базису, образованному некомпланарной тройкой векторов. Доказательство единственности такого разложения. Примеры.
1)Задача разложения вектора по базису, образованному некомпланарной тройкой векторов.
Пусть  – базис
– базис  и пусть
и пусть  произвольный вектор. Проведем следующие построения.
произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора  и вектор
и вектор 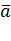 от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы
от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы  , плоскость
, плоскость  и плоскость
и плоскость  ; далее через конец вектора
; далее через конец вектора 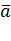 проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:

По правилу сложения векторов получаем равенство:  (1)
(1)
По построению  . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число
. Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число  , такое что
, такое что  . Аналогично,
. Аналогично,  и
и  , где
, где  . Теперь, подставляя эти равенства в (1), получаем:
. Теперь, подставляя эти равенства в (1), получаем:  (2)
(2)
и возможность разложения по базису доказана.
2)Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора 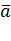 по базису
по базису  :
:
 и
и  . Тогда
. Тогда  (3)
(3)
Заметим, что по условию векторы  некомпланарные, следовательно, они попарно неколлинеарные.
некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая:  или
или  .
.
а) Пусть  , тогда из равенства (3) следует:
, тогда из равенства (3) следует:
 (4)
(4)
Из равенства (4) следует, что вектор  раскладывается по базису
раскладывается по базису  , т.е. вектор
, т.е. вектор  лежит в плоскости векторов
лежит в плоскости векторов  и, следовательно, векторы
и, следовательно, векторы  компланарные, что противоречит условию.
компланарные, что противоречит условию.
б) Остается случай  , т.е.
, т.е.  . Тогда из равенства (3) получаем
. Тогда из равенства (3) получаем  или
или
 (
(