Как складываются и перемножаются матрицы. Приведите примеры.
Складывать можно только матрицы одинакового размера.
Сложение матриц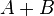 
есть операция нахождения матрицы 
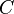, все элементы которой равны попарной сумме всех соответствующих элементов матриц 
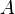и 
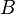, то есть каждый элемент матрицы 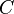равен
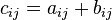
Количество столбцов в матрице 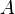должно совпадать с количеством строк в матрице 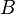, иными словами, матрица 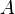обязана бытьсогласованной с матрицей 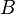. Если матрица 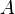имеет размерность 
, — 
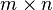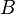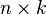, то размерность их произведения 
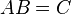есть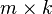 
.
| Найти матрицу C равную произведению матриц A = | 
| 
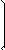
| и B = |
|
| . | ||||
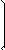
| -3 |
Решение:
| С = A · B = |
|
| · |
|
| = |
|
| ||||||
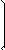
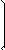
| -3 |
Элементы матрицы C вычисляются следующим образом:
c11 = a11·b11 + a12·b21 = 4·3 + 2·(-3) = 12 - 6 = 6
c12 = a11·b12 + a12·b22 = 4·1 + 2·4 = 4 + 8 = 12
c21 = a21·b11 + a22·b21 = 9·3 + 0·(-3) = 27 + 0 = 27
c22 = a21·b12 + a22·b22 = 9·1 + 0·4 = 9 + 0 = 9