Схемы для оценки погрешностей при измерении биений

При анализе составляющих погрешностей измерения радиального и торцового биений могут быть полезны схемы, позволяющие отобразить механизм появления погрешности и вывести аналитические зависимости для оценки значений этих погрешностей. Примером очевидной причины возникновения погрешностей является наклон линии измерения по отношению к ее идеальному направлению (рис. 6.1). В итоге возникает инструментальная составляющая погрешности (в приборах с фиксированным направлением линии измерения) или субъективная составляющая (при установке линии измерения на глаз). Как показывает опыт измерений, отклонения углов от номинального положения в последнем случае не превышает значений (2…3)°.

При измерении радиального и торцового биений погрешности из-за неизменного (постоянного) несовпадения линии измерения с номинальным направлением практически всегда будут пренебрежимо малы из-за малости углов наклона линии измерения и небольших измерительных перемещений. Более опасной является ситуация, когда направление линии измерения изменяется в процессе измерений (плоскопараллельная или угловая осцилляция линии измерения).

 

 

Для случая контроля годной детали наибольшее значение измерительного перемещения можно принять равным допуску биения.

Рассмотрим расчетную схему, которая позволяет оценить погрешности из-за отклонения направления фактической линии измерения (линия АС) от номинального направления линии измерения АВ на угол α(рис. 6.2).

 

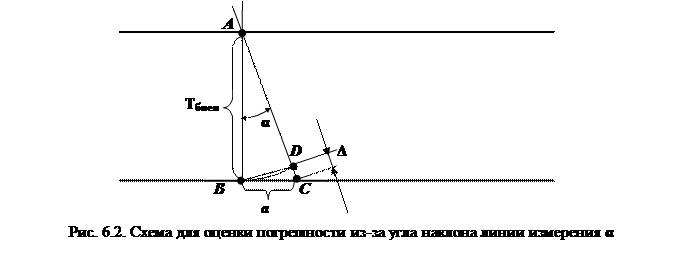
Отрезок АВ (максимальное перемещение измерительного наконечника) принимаем равным допуску биения, поскольку этим допуском ограничено перемещение наконечника при измерении биения годной детали. Результатом наличия угла α. будет дефектное перемещение Δ, равное отрезку DC, который дуга BD отсекает от стороны АС. Проведя хорду BD, стягивающую одноименную дугу, можно приближенно рассчитать значение Δиз треугольника BDC. Треугольник BDC можно принять за прямоугольный треугольник, подобный треугольнику АBC, с прямым углом BDC, и углом DBC = α.

Из треугольника BDC рассчитываем значение Δ, равное отрезку DC:

Δ = DC = BC·sinDBC = a·sinα.(6.1)

Поскольку a = BC = АBtgα, и АB = Т_биен, при Т_биен= Тможно записать:

Δ = Т· tgα · sinα,

что при малости углов αвследствие того, что tgα≈ sinα, можно представить в виде одной из двух следующих зависимостей:

Δ = Т· tg²α,(6.2)

Δ = Т· sin² α.(6.3)

Увеличение измерительных перемещений при больших значениях допусков биения приведет к росту только абсолютных значений погрешностей, относительные погрешности при неизменных значениях угла α будут одинаковыми.