Исходные данные к задаче представлены в таблице 1.

Рисунок 2

Решение:

В случае использования способа вращения вокруг проецирующей прямой следует помнить:

-плоскости проекций остаются неизменными, происходит перемещение объектов (от общего положения к частному);

-перемещаются при решении комплексных задач одновременно все объекты (точки, отрезки, плоские фигуры);

-ось вращения располагать перпендикулярно проецирующей плоскости (на эпюре – перпендикулярно оси Х);

-одна проекция объекта совершает вращательное движение, а другая перемещается параллельно оси Х.

 

Алгоритм решения задачи:

Кратчайшее расстояние от точки до прямой есть перпендикуляр, проведенный к этой прямой. Провести через точку перпендикуляр можно только к натуральной величине отрезка, поэтому задача сводится в первую очередь к определению натуральной величины отрезка.

1 Выбираем ось вращения О(О₁,О₂).

2 Вращаем проекцию отрезка В₁С₁ до положения параллельно оси Х. Достраиваем вторую проекцию отрезка и новое положение точки А. В результате получаем отрезок прямой уровня.

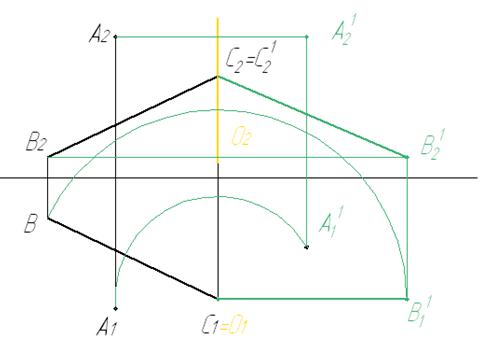
3 Используем теорему о проецировании прямого угла. Из точки А¹₂ опускаем перпендикуляр на отрезок В¹₂С¹₂ и находим вторую проекцию перпендикуляра.

4 Выбираем новую ось вращения и определяем натуральную величину перпендикуляра.