Понятие случайной величины. Закон распределения дискретной случайной величины
Определение 1. Случайнойназывается величина, которая в результате испытания принимает только одно значение из возможного множества своих значений, наперед неизвестное и зависящее от случайных причин.
Различают два вида случайных величин: дискретные и непрерывные.
Определение 2. Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное.
Другими словами, возможные значения дискретной случайной величину можно перенумеровать.
Описать случайную величину можно с помощью ее закона распределения.
Определение 3. Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями.
Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, в первой строке которой указаны в порядке возрастания все возможные значения случайной величины, а во второй строке соответствующие вероятности этих значений, т.е.:
| x | x1 | x2 | х3 | … | хn |
| p | р1 | р2 | р3 | ... | рn |
где р1+ р2+…+ рn = 1.
Такая таблица называется рядом распределения дискретной случайной величины.
Если множество возможных значений случайной величины бесконечно, то ряд р1+ р2+…+ рn+… сходится и его сумма равна 1.
Закон распределения дискретной случайной величины Х можно изобразить графически, для чего в прямоугольной системе координат строят ломаную, соединяющую последовательно точки с координатами (xi;pi), i=1,2,…n. Полученную линию называют многоугольником распределения (рис. 4.1).

Рис. 4.1
Закон распределения дискретной случайной величины Х может быть также задан аналитически (в виде формулы):
P(X=xi)=φ(xi),i =1,2,3…n.
Задача 4.1.Вероятности того, что студент сдаст экзамены в сессию по математическому анализу и органической химии соответственно равны 0,7 и 0,8. Составить закон распределения случайной величины Х - числа экзаменов, которые сдаст студент.
Решение. Рассматриваемая случайная величина X в результате экзамена может принять одно из следующих значений: x1=0, x2=1, х3=2.
Найдем вероятности этих значений. Обозначим события:
 – студент сдаст экзамен по математическому анализу;
– студент сдаст экзамен по математическому анализу;
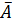 – студент не сдаст экзамен по математическому анализу;
– студент не сдаст экзамен по математическому анализу;
 – студент сдаст экзамен по органической химии;
– студент сдаст экзамен по органической химии;
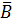 – студент не сдаст экзамен по органической химии.
– студент не сдаст экзамен по органической химии.
По условию:
 = 0,7 =>
= 0,7 =>  ) = 1 –
) = 1 –  = 0,3;
= 0,3;
 = 0,8 =>
= 0,8 =>  = 1 –
= 1 – 
Тогда:
P(x=0) =  ) =
) =  = 0,3
= 0,3  0,2 = 0,06.
0,2 = 0,06.
P(x=1) =  )=
)=  = 0,7
= 0,7  0,2 + 0,3
0,2 + 0,3  0,8 = 0,38
0,8 = 0,38
P(x=1)=  0,7
0,7  0,8 = 0,56.
0,8 = 0,56.
Итак, закон распределения случайной величины Х задается таблицей:
| x | |||
| p | 0,06 | 0,38 | 0,56 |
Контроль: 0,06+0,38+0,56=1.