Основные понятия комбинаторики

Глава 1. Вероятность случайного события

Элементы комбинаторики

Основные понятия комбинаторики

Комбинаторикой (комбинаторным анализом) называют раздел математики, в котором изучаются задачи выбора и расположения элементов из некоторого основного (обычно конечного) множества в соответствии с заданными правилами.

Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых правилами суммы и произведения.

Правило суммы. Если объект А может быть выбран из некоторой совокупности объектов m способами, а другой объект В – n способами, то выбрать либо А, либо В можно m+n способами.

Правило произведения. Если объект А может быть выбран из некоторой совокупности объектов m способами и после каждого такого выбора объект В может быть выбран n способами, то пара объектов А и В в указанном порядке может быть выбрана m · n способами.

Эти правила распространяются на случай трёх и большего числа объектов.

Кроме этих правил известны формулы, помогающие решать некоторые типовые задачи, встречающиеся довольно часто. Комбинациям, фигурирующим в этих задачах, присвоены особые названия – размещения, перестановки и сочетания.

Определение 1. Размещениями из n элементов по m (m ≤ n) элементов в каждом называются комбинации, содержащие по m различных элементов, выбранных из данных n элементов, которые отличаются либо составом, либо порядком входящих в них элементов.

Число всех возможных размещений из n элементов по m обозначается символом и вычисляется по формуле:

= n ∙ ( n – 1) ∙ … ∙ ( n – m + 1)= .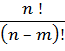

Определение 2. Перестановками из n различных элементов называются комбинации, состоящие из одних и тех же n элементов и отличающиеся только порядком расположения элементов.

Число всех возможных перестановок из n элементов обозначается символом и вычисляется по формуле:

= n ∙ ( n - 1) ∙ … ∙2 ∙1= n !

Нетрудно заметить, что перестановки из n элементов являются частным случаем размещений из n элементов по m, когда m = n, т.е. число элементов в комбинации совпадает с числом имеющихся элементов. Таким образом, справедлива формула:

= .

Определение 3. Сочетаниями из n элементов по m (m ≤ n) в каждом называются комбинации, содержащие по m различных элементов, выбранных из данных n элементов, которые отличаются составом входящих в них элементов. При этом порядок расположения элементов не играет роли.

Число всех возможных сочетаний из n элементов по m обозначается символом 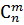и вычисляется по формуле:

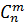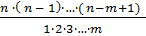= = , т. е. = .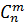

Свойства сочетаний:

= 1,

= ,

= + ,

+ + + … + = .

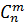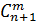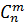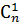Определение 4. Размещениями с повторениями из n элементов по m элементов в каждом называются комбинации, содержащие по m возможно повторяющихся элементов, выбранных из данных n элементов, которые отличаются либо составом, либо порядком входящих в них элементов.

Число всех возможных размещений с повторениями из n элементов по m обозначается символом 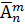и вычисляется по формуле:

= .
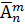