Операции над множествами
Существуют несколько основных операций над множествами, с помощью которых можно строить новые множества.
Объединениемдвух множеств А и Вназывается новое множество, содержащее все элементы из А и все элементы из В.
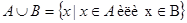
Пересечениемдвух множеств А и Вназывается новое множество, состоящее из тех элементов, которые принадлежат обоим множествам.
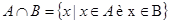
Разностьюдвух множеств А и В называется новое множество,содержащее те элементы из А, которые не принадлежат множеству В.
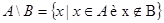
Если класс объектов, на которых определяются различные множества обозначитьU(универсум), то дополнением множестваАназывают разность 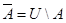 .
.
Симметрической разностью множеств А и В называется множество, содержащее все элементы А, не принадлежащие В, и все элементы В, не принадлежащие А.
 .
.
Операции над множествами могут быть проиллюстрированы на диаграммах Эйлера-Венна(см. рисунок 1 - 5).
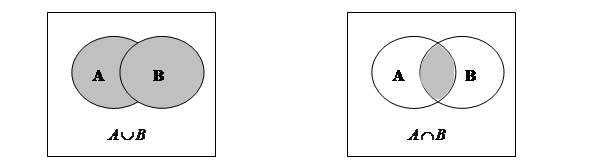
Рисунок 1 – Объединение множеств Рисунок 2 – Пересечение множеств

Рисунок 3 – Разность множеств Рисунок 4 – Дополнение множества
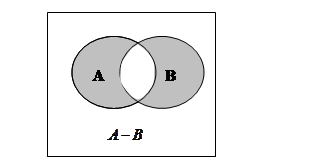
Рисунок 5 – Симметрическая разность множеств
Указанные операции обладают нижеследующими свойствами(законы алгебры множеств).
1. Идемпотентность (удаление одинаковых операндов):
1) 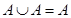 ; 2)
; 2)  .
.
2. Коммутативность (перестановка операндов):
1) 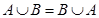 ;2)
;2) 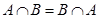 .
.
3.Ассоциативность (возможность бесскобочной записи).
1) 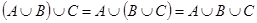 ; 2)
; 2) 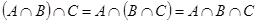 .
.
4. Дистрибутивность (раскрытие скобок):
1) 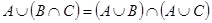 ; 2)
; 2)  .
.
5. Законы (правила) де Моргана:
1)  ; 2)
; 2) 
6. Законыпоглощения:
1) 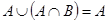 ; 2)
; 2) 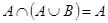 ;
;
3)  ; 4)
; 4) 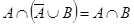 ;
;
5)  ; 6)
; 6) 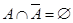 ;
;
7)  ; 8)
; 8) 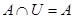 ;
;
9) 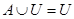 ; 10)
; 10) 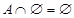 .
.
7. Закондвойного отрицания: 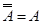 .
.
11. 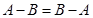 .
.
12. 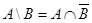 .
.
13. 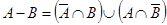 .
.
Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.
Пусть А и В - множества. Выражение вида (a,b), где  и
и  , называется упорядоченной парой. Равенство вида (a,b)=(c,d) означает, что a=c и b=d. В общем случае, можно рассматривать упорядоченную n-ку
, называется упорядоченной парой. Равенство вида (a,b)=(c,d) означает, что a=c и b=d. В общем случае, можно рассматривать упорядоченную n-ку 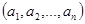 из элементов
из элементов 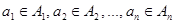 . Упорядоченные n-ки иначе называют наборами или кортежами.
. Упорядоченные n-ки иначе называют наборами или кортежами.
Декартовым (прямым) произведением множеств 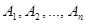 называется множество упорядоченных n-ок (наборов, кортежей) вида
называется множество упорядоченных n-ок (наборов, кортежей) вида 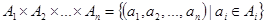 .
.
Степенью декартового произведения 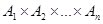 называется число множеств n, входящих в это декартово произведение.
называется число множеств n, входящих в это декартово произведение.
Если все множества  одинаковы, то используют обозначение
одинаковы, то используют обозначение  .
.
Разбиение множества -это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.
Покрытие -семейство множеств, объединение которых содержит данное множество.