Введение
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СЛАВЯНСКИЙ-НА-КУБАНИ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Кафедра математики и МПМ
Радченко С.А.
Методические рекомендации
по курсу
«Теория функций
Комплексной переменной»
Для студентов педагогических вузов очной формы обучения
специальность «Математика» и «Информатика»
Славянск-на-Кубани
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
СЛАВЯНСКИЙ-НА-КУБАНИ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Рекомендовано к печати Редакционно-издательским советом СГПИ
Радченко С.А. Теория функций комплексной переменной – Методические рекомендации к практическим занятиям по курсу «Теории функций комплексной переменной» – Славянск-на-Кубани, 2007г. – 36 с.
Пособие включает в себя основные разделы дисциплины ТФКП. Оно содержит определения основных понятий, соответствующие формулы, примеры решения типовых задач различной степени трудности, задачи для самостоятельного решения. Поможет при подготовке к практическим занятиям, зачетам, экзаменам. Предназначено для студентов математического факультета и преподавателей вуза.
Методические рекомендации соответствуют государственному стандарту высшего профессионального образования (ГОСВПО) и действующим программам и предназначены для студентов специальностей 030100 «Информатика» 010100 «Математика» очной формы обучения.
При составлении использовалась следующая литература:
1.Гусак А.А., Бричикова Е.А., Гусак Г.М. Теория функций комплексной переменной и операционное исчисление. – Мн.:ТетраСистемс, 2002. – 208с.
2.Сборник задач по математике для втузов. Ч.2. Специальные разделы математического анализа: Учеб. Пособие для втузов./Болгов В.А., Ефимов А.В. и др.; под ред. А.В.Ефимова, Б.П.Демидовича. – 2-е изд. – М.: Наука. Гл.ред.физ.-мат.лит.,1986. – 368с.
Введение
Данные методические рекомендации предназначены для обучения студентов вузов по разделу курса высшей математики «Теория функций комплексной переменной».
В пособии рассматриваются следующие вопросы: комплексные числа, их геометрическое изображение, действия над ними в алгебраической и тригонометрической форме, геометрическое истолкование этих действий; основные элементарные функции комплексной переменной, дифференцирование и интегрирование в комплексной области, функциональные ряды с комплексной переменной, особые точки.
Методические рекомендации содержат упражнения по всем изучаемым темам, примеры решения типовых задач с подробными указаниями к их решению. Рассмотрено около пятидесяти примеров. Студентам предлагается к самостоятельному решению девяносто упражнений, которые содержат около 900 задач.
Данное пособие предназначено для подготовки студентов к практическим занятиям, лекциям, к сдаче зачётов и экзаменов, так же пособие будет полезно преподавателям вузов.
Пространство комплексных чисел
Определение: Комплексным числом z называется упорядоченная пара  Выражение
Выражение  называют алгебраической формой комплексного числа. Число x - называют действительной частью, число у - называют мнимой частью.
называют алгебраической формой комплексного числа. Число x - называют действительной частью, число у - называют мнимой частью.
Обозначается действительная и мнимая части соответственно 
Если дано комплексное число  то число
то число  называют сопряженным числу
называют сопряженным числу 
1. Доказать ассоциативность произведения двух комплексных чисел.
2. Доказать ассоциативность суммы двух комплексных чисел.
3. Найти число противоположное комплексному числу.
4 Найти число обратное комплексному числу.
5 Даны три комплексных числа 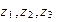 . Докажите, что
. Докажите, что
1. 
2. 
3. 

6 Получите формулу обращения операции умножения комплексных чисел
7 Убедитесь в выполнимости следующих свойств операции сопряжения:
1. 
8 Запишите действительную и мнимую часть комплексных чисел:
1.  2.
2.  3.
3.  4.
4. 
9 Запишите числа, сопряженные комплексным числам:
1.  2.
2.  3.
3.  4.
4. 
10 Запишите числа противоположные комплексным числам:
1.  2.
2.  3.
3. 

Комплексные числа в алгебраической форме
Над комплексными числами, заданными в алгебраической форме установлены следующие действия:



11 Выполните указанные действия над комплексными числами:
1.  2.
2.  3.
3.  4.
4.  5.
5.  6.
6.  7.
7.  8.
8. 
9. 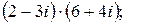 10.
10.  11.
11.  12.
12. 
Пример. Дано комплексное число z=3-4i. Найти число z  обратное числу z.
обратное числу z.
Решение. Так как  то
то

Пример. Найдите числа, обратные следующим комплексным числам:
1.  2.
2.  3.
3.  4.
4. 
Пример. Возвести в квадрат число z=3+4i.
Решение. Применив формулу квадрата суммы получим:

Замечание. При возведении комплексного числа в натуральную степень пользуются формулой бинома Ньютона.
12 Возведите в указанные степени данные комплексные числа, укажите действительную и мнимую части каждого комплексного числа:
1. 





7.  8.
8.  9.
9.  10.
10. 


13. 

 16.
16. 
Определение:Квадратным корнем из комплексного числа называют комплексное число, квадрат которого равен данному числу, т.е. 
Замечание. Исходя из определения можно получить, что  Тогда используя последние равенства получаем выражения для нахождения u и v:
Тогда используя последние равенства получаем выражения для нахождения u и v:

Из полученных равенств находят u, v, выбирая их знаки так, чтобы эти числа удовлетворяли равенству 
Пример. Извлечь квадратный корень из числа z=5+12i.
Решение. Обозначим квадратный корень из числа 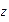 через
через  тогда
тогда  В данном случае
В данном случае 
 принимая во внимание замечание, находим:
принимая во внимание замечание, находим:


Таким образом получаем два значения квадратного корня из числа

13 Найдите значения квадратного корня из комплексного числа:
1. 




14 Решите квадратные уравнения:
1. 

3. 

15 Вычислите значения данных выражений при 
1. 

3. 

16 Вычислите:
1. 

 (n - натуральное число).
(n - натуральное число).
Тригонометрическая форма комплексного числа
Комплексному числу  соответствует точка
соответствует точка  комплексной плоскости
комплексной плоскости
Определение: Модулем комплексного числа  называют длину r отрезка
называют длину r отрезка  где
где  -начало кординат,
-начало кординат,  -точка, изображающая это комплексное число, т.е.
-точка, изображающая это комплексное число, т.е. 
Определение: Аргументом комплексного числа  называют величину угла наклона отрезка
называют величину угла наклона отрезка  к оси ОХ. Аргумент обозначают через
к оси ОХ. Аргумент обозначают через 
Определение: Главным значением аргумента комплексного числа называют единственное значение аргумента, заключенное между -  и
и  Обозначают
Обозначают 
Замечание. Аргумент комплексного числа удовлетворяет соотношениям

C помощью модуля и аргумента комплексное число можно представить в тригонометрической форме: 
где 
Замечание. Два комплексных числа равны тогда и только тогда, когда их модули равны, а аргументы отличаются на величину, кратную 2  т.е.
т.е.


Пример. Найти модуль и аргумент комплексного числа 
Решение.  По формуле
По формуле  вычисляем модуль данного комплексного числа
вычисляем модуль данного комплексного числа



17 Запишите в тригонометрической форме следующие числа:
1. 

 5; 5.
5; 5. 

7. 




Замечание. Комплексное число  можно представить в показательной форме. Принимая во внимание формулу Эйлера e
можно представить в показательной форме. Принимая во внимание формулу Эйлера e  получаем
получаем
 Правую часть этого равенства называют показательной формой комплексного числа.
Правую часть этого равенства называют показательной формой комплексного числа.
Пример. Записать комплексное число  в показательной форме.
в показательной форме.
Решение. Найдем действительную и мнимую части данного комплексного числа:

Находим модуль и аргумент полученного комплексного числа 

В соответствии с формулой, записываем данное число в показательной форме: 
18 Запишите в показательной форме следующие комплексные числа:
1.  4
4 
Пример. Докажите, что 
Решение. Воспользуемся формулой Эйлера e  При
При  эта формула примет вид e
эта формула примет вид e  . Так как
. Так как  то e
то e 
19 Докажите следующие равенства:
1. 


Рассмотрим два комплексных числа в тригонометрической форме

Замечание. Произведением комплексных чисел в тригонометрической форме является комплексное число вида:

Замечание. Частным комплексных чисел в тригонометрической форме является комплексное число вида:

Замечание. При возведении комплексного числа, заданного в тригонометрической форме в натуральную степень используют формулу Муавра:

20 Найдите произведение двух комплексных чисел:
1. 
2. 
21 Найдите частное двух комплексных чисел:
1. 
2. 
22 Возведите в указанную степень каждое из данных комплексных чисел:
1. 


4.  5.
5. 
Замечание. Арифметическое значение корня n-й степени из числа определяется следующей формулой:

Пример. Найти все значения квадратного корня из числа 
Решение. В соответствии с формулой находим

При k=0 получаем

При k=1 получаем второе значение корня

23 Найдите значения корня указанной степени из данных комплексных чисел:
1. 



5. 
 ; 7.
; 7. 
Пример. Доказать, что 
Решение. Воспользуемся формулой Муавра.  Тогда
Тогда

Так как

тогда получаем

откуда получаем 
24 Докажите следующие равенства:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
Замечание. Значения корня n-й степени из единицы определяются формулой:

25 Найдите все значения корня указанной степени из единицы:
1.  2.
2.  3.
3.  4
4  5.
5.  6.
6. 
26 Решите уравнения и изобразите на чертеже их корни:
1.  2.
2.  3.
3.  4
4 

5.  6.
6.  7.
7.  8.
8. 
Комплексная плоскость
27 Какое множество образуют точки, изображающие комплексные числа, для которых:
1. 




6. 

 10.
10. 
11. 
28 Запишите с помощью неравенств следующие множества точек комплексной плоскости:
1.полуплоскость, расположенная слева от мнимой оси;
2.второй квадрант;
3.полуплоскость, расположенная выше действительной оси на расстоянии не меньше 3;
4.полоса, точки которой отстоят от мнимой оси на расстоянии меньше 2;
5.квадрат с вершинами в точках 

6.прямоугольник с вершинами в точках -1, 

29 Выясните геометрический смысл следующих величин:


Пример. Какое множество точек z комплексной плоскости определяется равенством 
Решение. Модуль комплексного числа определяет расстояние точки, изображающей данное число, до начала координат. Поскольку  , то эти равенством определяется множество точек комплексной плоскости, удаленных от начала координат, на расстояние, равное 5. Таким образом, равенство
, то эти равенством определяется множество точек комплексной плоскости, удаленных от начала координат, на расстояние, равное 5. Таким образом, равенство  определяет окружность радиуса R=5 с центром в начале координат.
определяет окружность радиуса R=5 с центром в начале координат.
30 Приведите геометрическое описание всех точек комплексной плоскости, удовлетворяющих соответствующему соотношению:
1. 





 7.
7. 

 10.
10.  11.
11.  12.
12. 
13.  16.
16. 
17. 
Понятие функции комплексной переменной
Пусть  - область комплексной плоскости
- область комплексной плоскости  . Если каждой точке
. Если каждой точке  по определенному правилу
по определенному правилу  поставлено в соответствие единственное комплексное число
поставлено в соответствие единственное комплексное число  то говорят, что в области
то говорят, что в области  определена однозначная функция комплексной переменной
определена однозначная функция комплексной переменной  то есть
то есть  Функцию
Функцию  , можно рассматривать как комплексную функцию двух действительных переменных
, можно рассматривать как комплексную функцию двух действительных переменных  , определенную в области
, определенную в области  Задание такой функции равносильно заданию двух действительных функций
Задание такой функции равносильно заданию двух действительных функций  Таким образом, имеем
Таким образом, имеем

где 
31 Найдите значение функции  при z=1-i.
при z=1-i.
32 Докажите, что число z=1-i является корнем уравнения 
33 Найдите значения функции  при следующих значениях аргумента
при следующих значениях аргумента
1. 


34 Дана функция  Найдите ее значения при значениях аргумента:
Найдите ее значения при значениях аргумента:
1. 


35 Дана функция  Найдите ее значения при значениях аргумента:
Найдите ее значения при значениях аргумента:
1. 



36 Дана функция  Найдите ее значения при значениях аргумента:
Найдите ее значения при значениях аргумента:
1. 


37 При каких значениях z функция f(z)=z  равна нулю?
равна нулю?
38 Является ли число z=1+i корнем уравнения  ?
?
39 Найдите значение функции f(z)=  при z=1+i.
при z=1+i.
40 Докажите, что число z=1+i является корнем уравнения 
41 Найдите значения функции 
1. 

Определение: Множество точек расширенной комплексной плоскости  называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат данному множеству.
называется связным, если любые две его точки можно соединить непрерывной кривой, все точки которой принадлежат данному множеству.
Определение: Связное открытое множество точек комплексной плоскости называется областью.
Определение: Область D называется односвязной, если ее граница является связным множеством, в противном случае область называется многосвязной.
Пример. Указать область, определяемую условием

Решение. Так как  то
то  и
и  Получаем следующее неравенство
Получаем следующее неравенство

Возведем обе части неравенства в квадрат при условии  или
или  получаем
получаем

Таким образом, искомая область представляет собой открытое связное множество точек, ограниченное графиком параболы  и содержащее точку О
и содержащее точку О 
42 Описать области, заданные следующими соотношениями, и установить, являются ли они односвязными
1.  1
1 
 2
2 
 0
0 

5.  0
0 

 Re
Re 
43 Укажите на комплексной плоскости множество точек, удовлетворяющих указанным соотношениям:
1. 


4. 

44 Запишите с помощью неравенств следующие открытые множества точек комплексной плоскости:
первый квадрант;
левая полуплоскость;
полоса, состоящая из точек, отстоящих от мнимой оси на расстояние, меньшее трех;
внутренность эллипса с фокусами в точках  и большой полуосью, равной 3;
и большой полуосью, равной 3;
внутренность угла с вершиной в точке  раствора
раствора  симметричного относительно луча, параллельного положительной мнимой полуоси.
симметричного относительно луча, параллельного положительной мнимой полуоси.
Пример. Найти действительную и мнимую части функции 
Решение. Полагая  , находим
, находим
 Таким образом,
Таким образом, 
45 Для следующих функций найдите действительную и мнимую части:
1. 


4. 


Пример. Определите функцию w=f(z) по известным действительной и мнимой частям 
Решение. Если 
 то
то 
 Тогда
Тогда

Следовательно,

Таким образом, 
Замечание. Рассмотренный в задаче метод позволяет в общем случае получить для функции комплексной переменной выражение, зависящее от z и 

46 Определите функцию w=f(z) по известным действительной и мнимой частям:
1. 
2. 
3. 
47 Найдите образы указанных точек при заданных отображениях:
1. 

3. 

Замечание. Аналитический способ задания функции, т.е. с помощью формулы, в случае функций комплексной переменной часто приводит к многозначным функциям.
Определение: Говорят, что в области D определена многозначная функция w=f  если каждой точке z
если каждой точке z  поставлено в соответствие несколько комплексных чисел w.
поставлено в соответствие несколько комплексных чисел w.
Пример. Найти все значения функции  в точке
в точке 
Решение. Имеем  и
и  Тогда в соответствии с определением корня n-й степени из комплексного числа находим
Тогда в соответствии с определением корня n-й степени из комплексного числа находим

Таким образом,


48 Найдите все значения следующих функций в указанных точках:
1. 

3. 

49 Найти  если
если 
1. 


4. 

Предел и непрерывность
функции комплексной переменной
Определение: Число а  называется пределом функции
называется пределом функции  ,
,  и обозначается а=
и обозначается а=  если для любого
если для любого  найдется
найдется  , такое что для всех z
, такое что для всех z  удовлетворяющих неравенству
удовлетворяющих неравенству  выполняется неравенство
выполняется неравенство 
Определение: Функция  называется непрерывной в точке z
называется непрерывной в точке z  если она определена в этой точке и
если она определена в этой точке и 
Определение: Функция  , непрерывная в каждой точке области D, называется непрерывной в этой области.
, непрерывная в каждой точке области D, называется непрерывной в этой области.
Пример. Доказать, что функция  является непрерывной при любом значении z
является непрерывной при любом значении z 
Решение. Выберем произвольно некоторое значение z  и рассмотрим разность
и рассмотрим разность  Если
Если  то существует такое число М
то существует такое число М  0, при котором выполняется неравенства
0, при котором выполняется неравенства  Тогда получаем
Тогда получаем

Выберем в качестве  число
число  где
где  Из неравенства
Из неравенства  следует что
следует что

Таким образом, получаем , что  т.е по определению функция непрерывна в точке z
т.е по определению функция непрерывна в точке z  Точка z
Точка z  выбрана произвольно, значит функция
выбрана произвольно, значит функция  непрерывна в любой точке.
непрерывна в любой точке.
50 Докажите, что функция является непрерывной при любом значении z 
1. 



5. 

51 Как доопределить функции в точке z=0, чтобы они стали непрерывными в этой точке:
1. 



Замечание. Если представить  в виде
в виде  то запись а=
то запись а=  где z
где z  эквивалентна следующей:
эквивалентна следующей: 
Это позволяет определить предел f  через пределы действительной и мнимой частей.
через пределы действительной и мнимой частей.
Пример. Вычислить 
Решение. 


52 Вычислите следующие пределы:
1. 



Основные элементарные
функции комплексной переменной
Функции  определяются как суммы соответствующих степенных рядов, сходящихся на всей комплексной плоскости:
определяются как суммы соответствующих степенных рядов, сходящихся на всей комплексной плоскости:



Для функций  справедливы формулы Эйлера:
справедливы формулы Эйлера: 
откуда 
Если  то
то 
Замечание. Все формулы тригонометрии остаются справедливыми и для тригонометрических функций комплексной переменной.
Гиперболические функции  определяются формулами:
определяются формулами:

Логарифмическая функция Lnz, определяется как функция, обратная показательной. Эта функция является многозначной:

Обратные тригонометрические функции являются многозначными; они выражаются через логарифмические функции следующими формулами:



Общая степенная функция  определяется формулой:
определяется формулой:

Общая показательная функция  определяется формулой:
определяется формулой:

Пример. Доказать, что 
Решение. Принимая во внимание формулы  получаем:
получаем:

53 Докажите следующие равенства:
1. 
3. 

5. 

54 Докажите тождества:
1. 
 z; 3.
z; 3. 
Пример. Найти 
Решение. По формуле  находим
находим

55 Вычислите следующие значения:
1. 



5. 


9. 



Пример. Найти 
Решение. Имеем  главное значение аргумента arg
главное значение аргумента arg  , тогда в соответствии с формулой
, тогда в соответствии с формулой 


находим значение логарифмической функции 

Главное значение логарифма получим при k=0: 
56 Найдите все значения следующих логарифмов:
1. 


4. 


Пример. Найти значение 
Решение. Воспользуемся формулой 

Получаем

57 Найдите все значения обратных тригонометрических функций:
1. 




58 Найдите все значения степеней:
1. 2 



5. 


59 Выделите действительную и мнимую части следующих функций:
1. 


4. 


Пример. Найти аналитическое выражение для функции  при любом комплексном z. Вычислить Arccos2.
при любом комплексном z. Вычислить Arccos2.
Решение. Равенство  равносильно
равносильно  Тогда можем записать
Тогда можем записать 
Отсюда получаем e  Решая это квадратное уравнение относительно e
Решая это квадратное уравнение относительно e  уравнение, получаем
уравнение, получаем 
(здесь рассматриваются оба значения корня). Из этого равенства находим

Найдем Arccos2: 
60 Найдите аналитическое выражение для указанных ниже функций и для каждой из них найдите значение в соответствующей точке:
1. 


4. 

61 Найдите значения модуля и главное значение аргумента заданных функций в указанных точках:
1. 

3. 

Геометрический смысл модуля и аргумента производной
Пусть  - аналитическая в точке z
- аналитическая в точке z  функция и
функция и 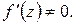 Тогда
Тогда 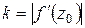 геометрически равен коэффициенту растяжения в точке z
геометрически равен коэффициенту растяжения в точке z  (точнее, при
(точнее, при 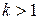 имеет место растяжение, а при
имеет место растяжение, а при  - сжатие). Аргумент производной
- сжатие). Аргумент производной  геометрически равен углу, на который нужно повернуть касательную в точке z
геометрически равен углу, на который нужно повернуть касательную в точке z  к любой гладкой кривой
к любой гладкой кривой  , проходящей через точку
, проходящей через точку  чтобы получить касательную в точке
чтобы получить касательную в точке  к образу
к образу  этой кривой при отображении
этой кривой при отображении  При этом, если
При этом, если  , то поворот происходит против часовой стрелки, а если
, то поворот происходит против часовой стрелки, а если  0, - то по часовой.
0, - то по часовой.
Пример. Найти коэффициент растяжения и угол поворота в точке  при отображении
при отображении 
Решение. Найдем производную функции и ее значение в точке  :
:

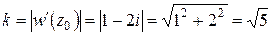
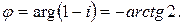
62 Найдите коэффициент растяжения и угол поворота для заданных отображений в указанных точках:
1. 


4. 


63 Найти множества всех точек z  , в которых при следующих отображениях коэффициент растяжения k=1:
, в которых при следующих отображениях коэффициент растяжения k=1:
1. 
 ; 3.
; 3.