Архимедова сила. Уравнение Бернулли

 

В отличие от твердого тела, жидкость — среда бесструктурная, ее микроскопическое устройство не содержит такой «несущей конструкции», как кристаллическая решетка. Соответственно, вопрос об ориентации поверхности, к которой приложено напряжение, здесь не возникает — все ориентации равноправны. Кроме того, в жидкости несравненно меньшую роль играют касательные напряжения. Если в твердом теле они ответственны за сдвиговые деформации и вполне проявляют себя в статике, то в жидкости касательные напряжения возникают исключительно в динамической задаче и лишь при учете диссипативного эффекта — вязкости.

Опыт показывает, что в гидростатике — науке о равновесии жидких тел — а равно и в консервативной (бездиссипативной) гидродинамике существен всего один вид напряжения — давление, обладающее свойством изотропности. Это и составляет содержание закона Паскаля: давление жидкости и газа передается одинаково во всех направлениях. Иными словами, давление — скалярная функция:

 

P= P(r). (8.18)

 

Одно из важнейших следствий изотропии давления было известно задолго

до Паскаля — это закон Архимеда: тело, погруженное в жидкость, выталкивается с силой, равной весу вытесненной жидкости. Рассмотрим тело А, плавающее в сосуде с жидкостью (рис. 8.8 а), и отдельно — сосуд, заполненный той же жидкостью до того же уровня, но без погруженного в него тела (рис. 8.8 б). Если жидкость, заполняющая полость а А' на рис. 8.8 б, пребывает в равновесии, то значит силы, действующие на полость А', как раз и

удерживают ее собственный вес. Ввиду скалярности давления (8.18) и отсутствия касательных напряжений, неважно, чем заполнена полость А', так что и на тело А будут действовать так же распределенные силы, имеющие ту же равнодействующую.

Рис. 8.8

 

Хотя приведенные выше рассуждения и дают нам аргументы в пользу закона Архимеда, они не могут считаться доказательством. В дополнение к ним хотелось бы дать современную трактовку архимедовой силы, пригодную для решения динамических задач. Мы сделаем это, опираясь на закон Паскаля. Пусть давлениие в жидкости или газе зависит от координаты:

P = P(x)

(рис. 8.9). Выделим мысленно в жидкости некоторый параллелепипед со сторонами dx, dy, dz, ориентированными по координатным осям. Тогда в напралении оси х на него будет действовать сила P(x) • dy dz, а навстречу ей — P(x + dx) • dy dz, суммарная же сила будет равна их разности, которая, в силу малости dx, может быть линеаризована:

 

F_x = P(x) dydz - P(x + dx) • dy dz =

- (dP/dx) • dxdydz + О(х).

Рис. 8.9

 

Удобно ввести понятие объемной плотности силы:

 

f_x = dF_x/dV = -dP/dx. (8.19)

 

Это и есть сила Архимеда. В случае зависимости давления от трех координат, вместо обычной производной в (8.19), следует использовать операцию градиента — см. (8.25).

Представим себе, например, несжимаемую жидкость в поле тяжести. При р(х) = const объемная плотность силы тяжести есть просто рg. Пусть ось х направлена вглубь жидкости. Запишем условие равновесия любого малого элемента объема dV:

 

ρgdV - (dP/dx) • dV = 0.

 

Сокращая dV и интегрируя, получаем хрестоматийный результат:

P = P₀ + ρgх, (8.20)

где Po — давление на поверхности жидкости. Из (8.20) можно получить решение упомянутых выше статических задач. Рассмотрим в качестве примера два открытых сосуда, соединенных посредством сифона (рис. 8.10). Давление жидкости в точке А,

с точностью до отношения ширины трубки к высоте ее над уровнем жидкости в сосудах h, равно

 

P₀ + ρgх_А =P₀- ρgh,

 

безоносительно к точке свободной поверхности, от которой мы отсчитываем х_А. Тем самым подтверждается, что в сосудах, соединенных так, как показано на рис. 8.10, жидкость в равновесии оказывается на одном уровне, а при нарушении этого условия должно возникнуть течение, перекачивающее жидкость в сосуд с более низким уровнем через трубку. На этом и основан принцип сифона. Рассмотрим эффекты, обусловленные работой давления. Прежде всего представим себе жидкость или газ, занимающие в состоянии равновесия некий цилиндр с площадью основания S (рис. 8.11 а). Давление в пределах данного цилиндрического объема будем считать постоянным и равным P.

Пусть одно из оснований смещается на малое расстояние dx, но при этом

 

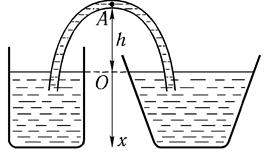
Рис. 8.10 два открытых сосуда, соединенных посредством сифона

 

количество текучего вещества внутри цилиндра сохраняется, т. е. жидкость

(газ) не течет через движущуюся границу. Сила давления вещества, заполняющего цилиндр, на границу равна P • S, соответственно, работа, совершаемая веществом при расширении, есть

δA = P S dx = P dV, (8.21)

где dV — изменение объема жидкости или газа. Если в процессе расширения

как-то изменится и давление, P —>• P + d'P, то это даст поправку в (8.21)

всего лишь второго порядка. Пусть теперь слегка меняет объем жидкое или

газообразное тело произвольной формы — на рис. 8.11 б начальное и конечное состояние показаны соответственно сплошной и пунктирной линиями. В силу закона Паскаля,

давление на любой участок границы действует в направлении нормали. Поэтому на любой малой площадочке, принадлежащей границе, мы можем построить цилиндрик с образу-

образующей, параллельной направлению нормали ξ (рис. 8.11 б).

Дальнейшие рассуждения аналогичны выводу (8.21), а затем можно вклад всех цилиндриков просуммировать (с учетом знака!) и получить тот же ответ:

Рис. 8.11

 

δA = P dV

где под dV подразумевается полное изменение объема жидкого элемента.

Рассмотрим стационарное течение жидкости или газа без диссипации. Вы-

Выделим некоторую трубку тока (рис. 8.12).

 

 

 

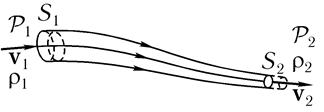
Рис. 8. 12

 

Пусть S₁ и S₂ — два произвольных сечения, нормальных к потоку, ρ₁, v₁ и ρ₂, V₂ — соответственно, плотность и скорость в сечениях S₁ и S₂. За время dt через сечение S₁ протек объем S₁v₁ dt, при этом втекающий газ совершил работу Р₁S₁v₁ dt. За то же вре-

время из сечения S₂ вытек объем S₂v₂ dt, совершив при этом работу P₂S₂v₂ dt над всем вытекающим газом. При стационарном течении массы ρ₂S₂v₂ dt и ρ₁S₁v₁dt, очевидно, равны. Введем плотность энергии текучей среды:

dE/dV = ρε + ρv²/2,

где ε включает отнесенную к единице массы внутреннюю энергию плюс энергию во внешних полях, т. е. всю энергию, кроме кинетической, плотность которой равна ρv²/2. Поскольку мы положили диссипативные эффекты несущественными, используем закон сохранения энергии:

 

 

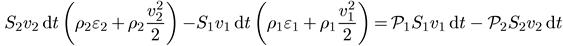
(8.22)

Разделим это уравнение почленно на величину dm протекающей через сечение за время dt массы. Удобно первый член левой части и второй член правой части (8.22) разделить на dm = ρ₂S₂v₂ dt, а второй член левой части и первый член правой части (8.22) разделить на dm = ρ₁S₁v₁dt. В результате получаем уравнение Бернулли

 

 

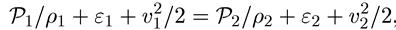
или, что то же,

 

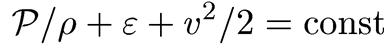
(8.23)

 

Важный частный случай уравнения Бернулли — течение в поле силы тяжести при неизменной массовой плотности внутренней энергии (для идеального газа это обусловлено постоянством температуры). Тогда

 

dE/dV = ρgh + ρv²/2,

 

где h — высота по отношению к некоторому заранее определенному нулевому уровню. Как следствие, получаем

 

P/ρ + gh + v²/2 = const. (8.24)

 

Если к тому же, жидкость несжимаема, то (8.24) можно использовать в виде

 

P + ρgh + pv²/2 = const. (8.25)

 

Именно эту форму записи чаще всего связывают с именем Бернулли; подчеркнем, однако, что уравнение (8.23) гораздо более универсально.

Уравнение (8.25) позволяет легко получить формулу Торричелли для скорости вытекания несжимаемой жидкости из сосуда через малое отверстие (она, правда, была выведена за сто лет до уравнения Бернулли). Постановка задачи ясна из рис. 8.13. Пусть высота

уровня воды в сосуде равна h₁, а высота, на которой расположено отвестие — h₂, так что h₁ - h₂ = h. Отверстие должно быть достаточно малым, чтобы выполнялось условие h << v. Из уравнения непрерывности (8.14) легко усмотреть, что для этого необходимо, чтобы

 

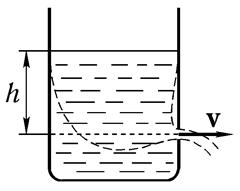
Рис 8 13

сечение отверстия было много меньше сечения сосуда. Таким образом обеспечивается с необходимой точностью, во-первых, стационарность течения и тем самым применимость уравнения Бернулли. Во-вторых, при медленном вытекании мы можем избежать вихревых течений, что позволяет рассматривать наше течение как одну-единственную трубку тока (обозначена пунктиром на рис. 8.13). Это очень важный аспект данной задачи; напомним, что уравнения (8.23)-(8.25) задают инвариант только в пределах трубки тока, который не всегда можно распространить на поток как целое.

Итак, ρ(h₁) = ρ(h₂), на уровне h₁ v ~ 0, а на уровне h₂, как следует

из (8.24),

 

v = √(2gh), (8.26)

 

т. е. скорость вытекания несжимаемой жидкости из малого отверстия совпадает со скоростью тела, свободно упавшего с высоты h. Это и есть формула Торричелли.

Отметим в заключение, что величина ρv²/2 иногда называется динамическим давлением, а формула (8.25) трактуется как инвариантность суммы статического и динамического давлений. В стационарном потоке несжимаемой жидкости давление P должно быть меньше там, где больше скорость.

Так объясняют принцип работы пульверизатора, эффект «присасывания» кораблей при близком прохождении параллельными курсами и т. д.